ChunkyGAN 水记（人脸的分块编辑，强泛化性）

ChunkyGAN 水记（人脸的分块编辑，强泛化性）

《ChunkyGAN: Real Image Inversion via Segments》

论文：https://dcgi.fel.cvut.cz/home/sykorad/Subrtova22-ECCV.pdf

项目：https://github.com/futscdav/Chunkmogrify

可以看到，有很强的泛化性，连带着口罩都能反演出来

ChunkyGAN 是一种基于反演的图像编辑技术，具有很强的鲁棒性和泛化性。

特殊之处在于，分块反演。对每个块，分别反演一个 latent，这样可以针对性的编辑某一个块的 latent 。

优势是，这样大大提高了泛化性和鲁棒性，被口罩遮住的脸、被手遮住的脸、雕像的脸都可以成功反演，并且能很好地编辑。（甚至狗脸都能成功反演）

本方法是一种对一般的 projection 方法的扩展，可以适用于任何 projection 方法

需要准备一个预训练的 GAN 、（基于优化的）反演算法、操作 latent 的方法

用户提供一个人脸图 $I$ ，以及对应的分割图 $S=\{S_i{\}}_{i=1}^n$ ，将原图分割为 $n$ 块

寻常的人脸编辑是，将人脸反演回 latent ，于是我们操作该 latent 修改图像

本方法是，由于人脸被用户分割为 $n$ 块，我们对每块分别反演出一个 latent，于是用户可以选择要操作的块，针对性的操作其 latent

反演时，使用 LPIPS 衡量重建质量。

用户提供的分割图不直接用（不是恒定不变的），而是在反演过程中参与优化，该过程有点复杂。

优化分割图时，不是直接优化像素，而是优化一个 分割隐编码 $X^S$ 。我们用一个分割生成网络 $G^S$ 来把 分割隐编码 $X^S$ 变为 $n$ 个分割图 $S$ 。分割生成网络 $G^S$ 是一个基于 StyleGAN2 的 DatasetGAN，需要进行预训练。反演时只优化 分割隐编码 $X^S$ ，不优化 分割生成网络 $G^S$ 。

预训练 $G^S$ 的方法是，先用 StyleGAN2 生成一个几十张图片数据集，然后用 [8] 的技术，将用户提供的分割图作为示例，对生成的图片进行标注，然后用这个数据集训练 分割生成网络 $G^S$ 。（不清楚是只训练 StyleGAN2 的 mapping 网络，还是整个一起训练，感觉描述有点歧义，我觉得更可能是整个一起训练）

不直接优化分割图，我认为是为了保护分割图不被破坏，作为一个约束，保持分割图一直处于 $G^S$ 的流形上。

至于为什么要优化分割图，我认为是在编辑人脸的过程中，五官位置会移动，如果分割图不能跟着动的话，就会导致问题，比如多出几个眼睛，或者是拼接边缘太明显。

这个分割图的优化流程实在是有点复杂了，而且用了非常强的人脸先验，导致这个技术很难再用于人脸之外的编辑了。

方法

我们的方法接受一个图像 $I$ ，用一系列 分割mask 和对应的 隐编码 将其重建。

分割mask为 $S=\{S_i{\}}_{i=1}^n$ ，其中每个像素都是0到1之间的连续值，所有像素的值加起来等于1。

隐编码为 $X^I=\{X_i^I{\}}_{i=1}^n$ ，与分割mask 一 一 对应。

多个隐编码被一个共享的生成器 $G^I$ 翻译为多个图像，再通过像素的线性混合得到输出图像，如图2所示：

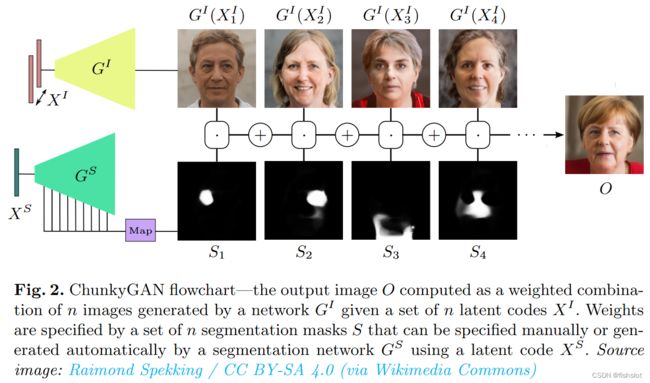图2：可以看到图中提供了多个latent，每个latent都生成了一张图片，我们用mask相当于在控制不同部分的透明度，将所有图片混合在一起，就得到了最终输出的图片。

输出图片的计算方式如下：

$$O\left(X^I,S\right)=\sum _{i=1}^n{G}^I\left(X_i^I\right)\cdot S_i$$

可以发现这个式子对 $X$ 和 $S$ 都是可微的。用 $I$ 和 $O$ 之间的不相似度来优化，就像在单分割重建的情况下一样。在本论文中，我们使用 LPIPS感知损失。

由于语义分割不是通用的，在不同人脸之间会有很大差异，所以有必要对 mask 进行优化。直接在像素上做优化会很浪费内存，而且也没有利用我们对问题已有的领域知识。于是，我们用一个分割生成器 $G^S$ ，从一个 分割隐编码 $X^S$ 产生 mask ，即 $S_i=G^S(X^S{)}_i$ 。（至于如何从单个 $X^S$ 生成多个 mask，可以倒回去看看图2 ）

本文中，我们使用的 分割生成器 $G^S$ 基于 DatasetGAN [27] 网络。该网络由一个 StyleGAN2 和一个 mapping 网络 组成。mapping 网络在一个适量的数据集（几十张图像）上训练，该数据集是由 StyleGAN2 随机生成的图片，并且由基于示例的合成来产生标注 [8] ，使用单个人工标注的图像作为示例。

最后，完整的优化目标如下：

$$\underset{X^S,X^I}{\min }{\mathcal{L}}_{\mathrm{LPIPS}}\left(I,\sum _{i=1}^n{G}^I\left(X_i^I\right)\cdot G^S{\left(X^S\right)}_i\right)+{\lambda }_{reg}\sum _{i=1}^n{\Vert X_i^I-X_{\mu }^I\Vert }_2^2$$

其中， $X_{\mu }^I$ 表示 平均隐编码，所以正则项的意思是，令所有 $X_i^I$ 尽量集中在一起。

这个正则项可以避免隐编码之间距离太远，从而能产生更真实的图像。这在 projection 阶段一般不会有什么影响，但是在编辑阶段，距离太远的隐编码会很快在外观上出现分歧。这种现象是因为预训练的编辑方向在视觉一致性上有限制（啥意思？）。

我们的方法与具体隐空间无关，通常来说可以使用任意隐空间的组合，只要其能够将输入图片映射为一个紧凑的编码。对于 StyleGAN ，我们考虑 $\mathcal{W}$ 空间、 ${\mathcal{W}}^{+}$ 空间 [1]、 $\mathcal{S}$ 空间 [23] 当然，不是非要用这些，任何以前发表的、新发表的、甚至是混合的方法都可以用。事实上，我们的方法是一种补充和扩展，可以让任意 projection 方法都得到比原来更好的结果。

这个过程的速度与 segment 的数量、还有优化步数有关。当 DatasetGAN 与 多分割 联合优化时，一次 projection 可能需要几分钟。当进行交互式编辑时，用户一次编辑一个 segment ，可以做到实时交互。

实验

嗯，看起来很强，但是我选择摸了