【医学信号处理与MATLAB（4）】主成分分析法-PCA

本节主要介绍的是多变数分析中的主成分分析法（PCA）

多变量分析

这一部分ppt上讲的很清楚了，故直接放ppt就好
需要注意的是：每一列代表的是一个channel，而不是每一行！

方差、协方差与相关性

双变量的数据与相关系数的关系

[MATLAB RULE]使用COV和CORRCOEF

多变量分析

主成分分析法(PCA)

数据量(DATA)与信息量(INFORMATION)

• 庞大的数据量≠庞大的信息量，通常资料中会夹带着许多不必要的噪声或者是意义较低或重复性高的信息。

主成分分析法的目的：

• 将资料通过旋转与线性混合的概念，找到新的basis来更有效地描述信息。
• 在失去最少信息的条件下，尽可能降低变量数目。
• 将数据中信息量较低的成分或者噪声去除。

数据冗余(REDUNDANCY)

所谓数据冗余，即数据中有一些信息是可以丢掉的。
以一个简单的概念为例。我们都知道一个垂直运动的弹簧，如果把它想象成有两个变量，但是这两个变量的相关性是非常高的，及数据冗余性太高(协方差大)。反之，数据冗余性就低(协方差小)。
我们想要做的，就是将冗余性高的数据投影到一个新的平面上(通过线性变换的方式)，让它的协方差=0，即不相关。

协方差矩阵(COVARIANCE MATRIX)

概念

我们希望经过线性变换后的协方差矩阵

• 对角元素，数值越大→包含越多信息
• 非对角元素，数值越小→冗余量越低(即各变量之间互不相关，每个变量都拥有存在的必要性)
  
  可以说，我们希望把协方差矩阵做一个对角化的动作
• 【对角化方法】：奇异值分解(有时间专门开篇文章解释一下)

实例说明

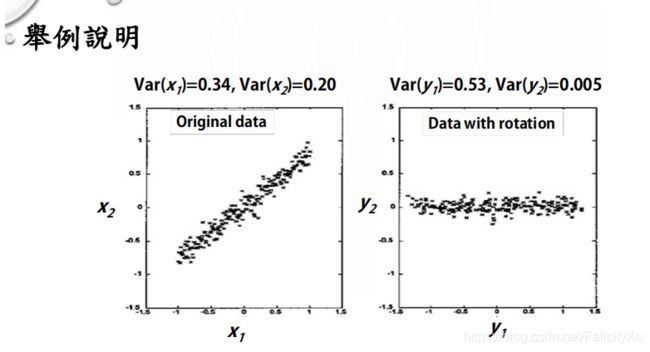
我们可以看到如下一幅图：

上左图中，变量x1和x2的具有很高的相关性，协方差为0.61544；如果通过PCA把矩阵做一个旋转，可以发现协方差能够接近0，相关性很低，并且y1的方差很大，y2的方差很小。
这就说明我们可以把y2丢掉，直接用y1来描述数据集。

再看一个例子：

在上图中，丢掉y2的信息其实是一个非常好的选择，而丢掉y1相对来说就没那么好了。

PCA实例的MATLAB代码

clear,close all
clc

%% create data
X = [2.50  2.40;
     0.50  0.70;
     2.20  2.90;
     1.90  2.20;
     3.10  3.00;
     2.30  2.70;
     2.00  1.60;
     1.00  1.10;
     1.50  1.60;
     1.10  0.90];  %[x1 x2]

[n m]=size(X);   %n measurements;m variables

X = X - ones(n,1)*mean(X,1); %subtract mean直接减去均值，接下来就可以在计算协方差的时候直接求平方了

CovX = cov(X);  %计算协方差矩阵

figure,plot(X(:,1),X(:,2),'o');  %绘图
xlabel('x_1'),ylabel('x_2')
title(['The covariance = ' num2str(CovX(2))])
axis([-2 2 -2 2])

%% calculate eigenvalues and eigenvectors
[eigVec,eigVal]=eig(CovX)
eigVec=fliplr(eigVec);  %fliplr函数，将数组从左向右翻转

%% project data to the eigenvectors
PCfull = X * eigVec;  %project data using full eigVec  旋转

Covfull = cov(PCfull)

figure, plot(PCfull(:,1),PCfull(:,2),'o')  %绘图，投影1
xlabel('y_1'),ylabel('y_2')
title(['Project data using full eigenvectors, The covariance = ' num2str(Covfull(2))])
axis([-2 2 -2 2])

PClarge = X * eigVec(:,1);  % project data only using the eigVec with largest eighVal

figure, plot(PClarge(:,1),zeros(n,1),'o')  %绘图，投影2
title('Project data only using the eigenvectors with largest eigenvalue')
xlabel('y_1')
axis([-2 2 -2 2])

PCsmall = X * eigVec(:,end);  % project data only using the eigVec with smallest eighVal

figure, plot(zeros(n,1),PCsmall(:,1),'o')   %绘图，投影3
title('Project data only using the eigenvectors with smallest eigenvalue')
ylabel('y_2')
axis([-2 2 -2 2])

%% reconstruct new X only using 1st eigenvector
newX = PClarge * eigVec(:,1)';   %重构
       
CovnewX = cov(newX)

figure, plot(newX(:,1),newX(:,2),'o'), hold on    %绘图，重构之后的图像
title(['The covariance of new X = ' num2str(CovnewX(2))])
xlabel('x_1'),ylabel('x_2')

可能不太清楚的代码的地方：
①ones(10,1)*mean(X,1)复制平均值，就不用做for循环了

②CovX = cov(X);协方差很高，相关性很高

③[eigVec,eigVal]=eig(CovX)返回一个列矢量，其中包含方阵A的特征值
视频里老师并没有介绍这一块相关的数学知识，所以补充一下：
关于特征值和特征向量，可以看一下这个问题下各个答主的回答：
如何理解矩阵特征值？
关于奇异值分解，可以看看这篇：
奇异值分解（SVD）

我们可以用第一列eigVec投影，也可以用第二列
上述的代码看看就好了，真正要学会使用的是下一个。

[MATLAB RULE]使用PRINCOMP

首先贴上MATLAB中对该函数的解释：

使用方法：[eigenVec,PC,eigenVal]=princomp(X)

• X is an N-by-P data matrix with N observations and P variables
• eigenVec：eigenvectors of cov(X)，对角线数值，代表每个主成分的方差，通常算完之后会按从大到小排列，越大代表越重要。eg五个通道最多能够解析出5个主成分,小的可以理解成为噪声
• eigenVal：eigenvalues of cov(X)
• PC：principal components of X

使用PRINCOMP进行PCA分析与去噪声

概念

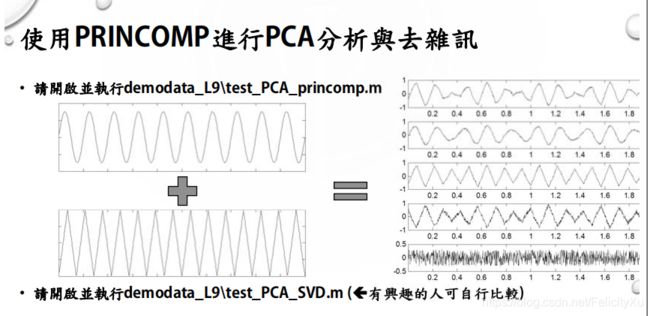
我们生成两个信号，一个正弦波，一个三角波，右边是通过给正弦波和三角波不同的权重从而生成的四个信号，最后一个是噪声。
现在的问题是，假设我们现在手上只有右边的五个信号，我们能不能利用PCA来还原出左边的两个信号呢/或者去除一些噪声？
这里附上连接PCA的数学原理

MATLAB代码

以使用包装好的princomp函数为例：
目的：找出不重要的主成分丢掉，还原出重要的主成分

clear, close all
clc



%% initialize parameters
samplerate=500; % in Hz
N=1000; % data length

freq1=5; % in Hz
freq2=7; % in Hz
taxis=[1:N]/samplerate;

PCnum=2;  % the number of PC used to reconstruct signals



%% generate test signals 
C1 = 0.75*sin(2*pi*freq1*taxis);        % 1st component: a sine wave
C2 = sawtooth(2*pi*freq2*taxis,0.5);    % 2nd component: a triangular wave

% Combine data in different proportions
X(1,:) = 0.5*C1 + 0.5*C2 + 0.1*rand(1,N);
X(2,:) = 0.7*C1 + 0.2*C2 + 0.1*rand(1,N);
X(3,:) = 0.2*C1 + 0.7*C2 + 0.1*rand(1,N);
X(4,:) = -0.3*C1 - 0.6*C2 + 0.3*rand(1,N);
X(5,:) = 0.6*rand(1,N);    % Noise only

% Center data by subtracting mean
X = X - mean(X,2)*ones(1,N);

figure, 
for i=1:size(X,1)
    subplot(size(X,1),1,i)
    plot(taxis,X(i,:)),xlim([taxis(1) taxis(end)])
end



%% Principal Components Analysis using princomp funcion (using eig and svd)
[U,PC,eigenVal]=princomp(X')

for i=1:size(X,1)     %计算主成分所占的比例，是累积计算的
    eigen_perc(i)=sum(eigenVal(1:i))/sum(eigenVal)*100;  % calculate accumulated percentage of eigenvalues
end

figure,    %这里画出了线性变换后五个主成分的图，去run一下demo可以发现，只有两个成分看起来像信号，其它三个成分都是噪声，所以我们可以只用前两个成分来还原信号
for i=1:size(PC,2)
    subplot(size(PC,2),1,i)
    plot(taxis,PC(:,i)),xlim([taxis(1) taxis(end)])
end

figure,plot(eigen_perc,'-o')   %计算主成分所占的比例的曲线,
xlabel('dimension'),ylabel('percentage of accumulate eigenvalues')



%% Check the covariance of principal components (PC)
cov(PC)  % make sure if the PCs are uncorrelated !这里肯定是一个对角阵
！
% the off-diagonal terms should be 0

%% Reconstruct the Signal only use the first PCnum PCs
newX = U(:,1:PCnum)*PC(:,1:PCnum)'; %看你想保留几个成分进行新信号的重构

figure, 
for i=1:size(newX,1)
    subplot(size(newX,1),1,i)
    plot(taxis,X(i,:)),hold on
    plot(taxis,newX(i,:),'r'),xlim([taxis(1) taxis(end)])
end
%可以看出，PCA的作用就是把不重要的主成分给去掉了，相当于去除了信号中的一些噪声（如我们之前在每个channel中利用randn函数生成的噪声），但是原始信号是还原不出来的

比较UNCORRELATED与INDEPENDENT

PCA少了一个非常关键的步骤就是：我们想知道原始信号长什么样，即原始的正弦波和三角波

如图所示，左边是原始的信号，右边是我们利用PCA还原出来的主成分PC1和PC2的样子。虽然它们两个是不相关的，但是还是没有分开得很好。
即，两个主成分虽然是不相关的，但是并不是独立的
所以我们需要分析出它的独立成分！！！！
然而，在ICA之前，做PCA也是非常必要的~