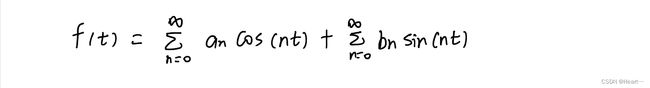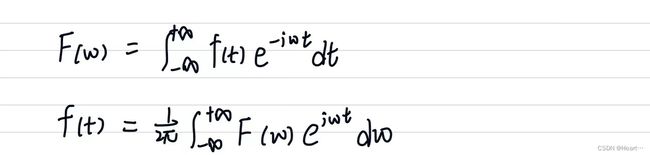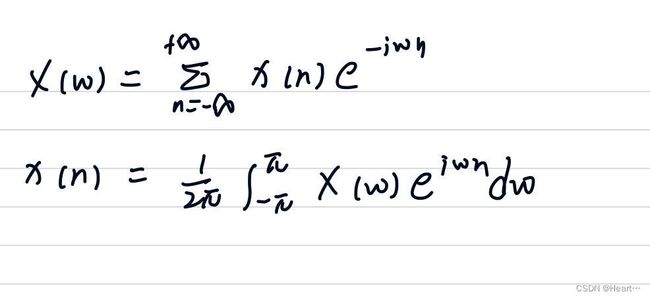浅谈五种傅氏变换

1.FS（傅里叶级数）

应用场景：时域周期连续信号，对应频谱非周期离散

任意连续周期信号均可用三角函数的线性组合来表示

我们默认信号周期为 2π,周期记作T1。 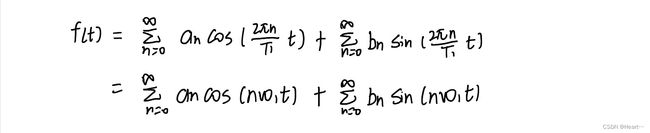  故 f（t）可以频谱看作由无限个频率为0，w,2w,3w....的正弦和余弦信号组成。

故FS的时域是周期连续信号，对应频谱为非周期离散的。

注：两周期信号相加，当且仅当两个周期信号周期之比为有理数时，相加之和才为周期信号。

举例来说：                

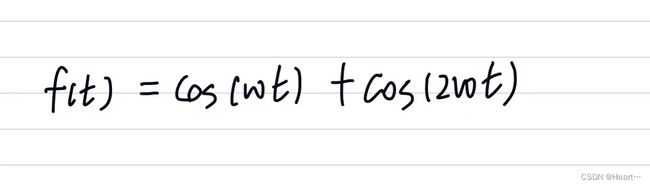它的时域信号是周期且连续的，而他的频率有w，2w组成，是离散且非周期的。

下面来图例来说：

 对于傅里叶的公式，我们习惯用复数形式展开，即复数形式的傅里叶级数展开形式为

2.FS(连续时间傅里叶变换)

应用场景：时域非周期连续信号，对应频谱非周期连续

对于非周期的连续信号，我们可以将其看作周期为无限大的周期信号，即T1趋于正无穷。这可以看作是傅里叶级数的推广，仍能用傅里叶级数展开，不过我们需要考虑极限的情况了。

可以写出复数形式的连续时间傅里叶变换展开形式

我们可以明显的发现，相对于傅里叶级数的展开式，w1由求和变为积分了，频率也由nw1变为了w，即由于T1趋于无穷而导致的(w1=2π/T1)。

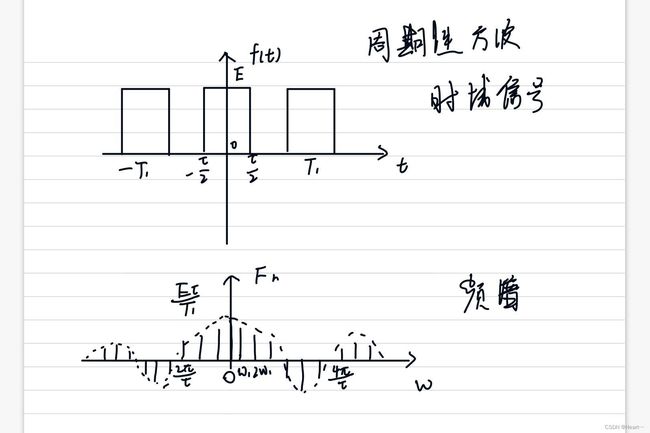
下面用一个周期内的方波信号来说明：

 对比傅里叶级数的频谱图，可以发现该图为其的包络。

3.DTFT(离散时间傅里叶变换)

应用场景：时域非周期离散信号，对应频谱周期连续

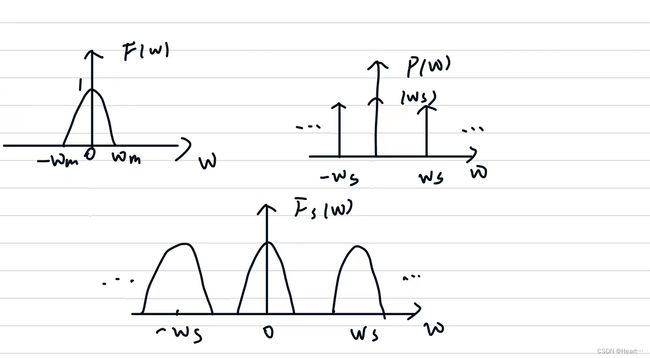
 对于非周期离散信号可由非周期连续信号在时域上乘上采样函数。注：采样函数的频谱还是采样函数。

 如果在时域上采样函数的脉冲间隔为Ts，那它的频域脉冲间隔为ws=2π/Ts。

注：1. 时域相乘为频域卷积。

 2. 一个函数与冲激函数卷积相当于把它搬到冲激函数所在位置。

频谱是周期连续的。周期是由采样导致的，连续是非周期连续函数导致的。

 复数形式的离散时间傅里叶变换展开形式

 这里我们可以看到，正变换式为级数求和，逆变换式是求积分。这也表明时域是离散的，频域是连续的。

下面我将用傅里叶变换之间的关系来引出DFT,DFS.

1.由傅里叶变换(FT)演化出离散时间傅里叶变换(DTFT)

傅里叶变换：

 由采样定理知，序列可以看作在满足采样定理的条件下对连续信号进行采样得到

 将时域间隔单位归一化后

 上式是将连续傅里叶变换中的时域信号进行离散化后得到，称离散时间傅里叶变换。下面我们将频域信号进行离散化。演化出DFT。

由于特殊符号不容易用键盘打出，下面采用特殊编辑器导出图片来说明。

2.离散时间傅里叶变换(DTFT)演化出离散傅里叶变换（DFT）

 上式在频域内也是离散且有限的，给出的是非周期离散序列的离散傅里叶变换。

3.傅里叶级数（FS）演化出离散傅里叶级数（DFS）

 上式即离散傅里叶级数

4 离散傅里叶级数（DFS）演化出离散傅里叶变换（DFT）

上式本质上与离散傅里叶变换（DFT）相同，仅差一个1/N。由此可见，离散傅里叶变换(DFT)可以从DTFT延伸而来，也可以认为是从DFS演变得到。

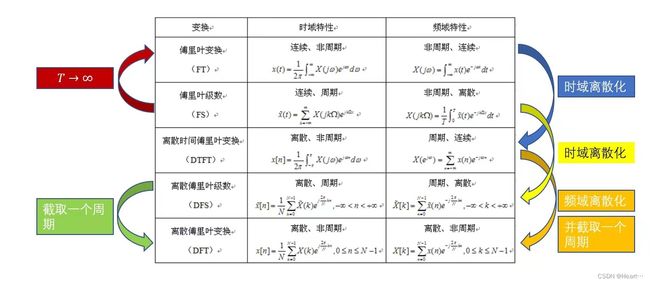
下面用图来展示它们之间的关系

可以观察到：除了截取周期的DFT，计算公式带积分的是非周期的，计算公式带累加符号的是周期的。

 

 

结合前述特性图示可知，除离散傅里叶变换外，若某个信号在时域（或频域）内是周期的，则经变换 （或反变换）后其变换结果在频域（或时域）内是离散的；若信号在时域（或频域）内是离散的，则其变换（或反变换）结果在频域（或时域）内是周期的。周期性和离散性呈现出对偶关系。

离散傅里叶变换（DFT）提供了一种在时域和频域内均是离散的信号变换方法。

计算机一般处理的都是离散信号，离散傅里叶变换就很符合这个特点。

 

 参考原文链接：http://t.csdn.cn/8N1dO