NNDL 作业10:第六章课后题(LSTM | GRU)
目录
习题6-3 当使用公式(6.50)作为循环神经网络得状态更新公式时,分析其可能存在梯度爆炸的原因并给出解决办法.
习题6-4 推导LSTM网络中参数的梯度,并分析其避免梯度消失的效果
习题6-5 推导GRU网络中参数的梯度,并分析其避免梯度消失的效果
附加题 6-1P 什么时候应该用GRU? 什么时候用LSTM?
附加题 6-2P LSTM BP推导,并用Numpy实现
总结
习题6-3 当使用公式(6.50)作为循环神经网络得状态更新公式时,分析其可能存在梯度爆炸的原因并给出解决办法.
公式是:![]() 还会存在两个问题
还会存在两个问题
(1)梯度爆炸问题:令![]() 为在第k时刻函数g(·)的输入,在计算公式
为在第k时刻函数g(·)的输入,在计算公式![]() 中的误差项
中的误差项![]() 时,梯度可能会过大,从而导致梯度爆炸问题
时,梯度可能会过大,从而导致梯度爆炸问题
(2)记忆容量问题:随着ht不断累积存储新的输入信息,会发生饱和现象。假设g(·)为Logistic函数,则随着时间t的增长,ht会变得越来越大,从而导致h变得饱和,也就是说,隐状态ht可以存储的信息是有限的,随着记忆单元存储的内容越来越多,其丢失的信息也就越来越多。
解决方法:在公式6.50的基础上引入门控机制来控制信息的累积速度,包括有选择地加入新的信息,并有选择地遗忘之前累积的信息。
习题6-4 推导LSTM网络中参数的梯度,并分析其避免梯度消失的效果
遗忘门:
![]()
输入门:
以及t时刻的Cell 状态(长时)方程:
![]()
输出门:
![]()
![]()
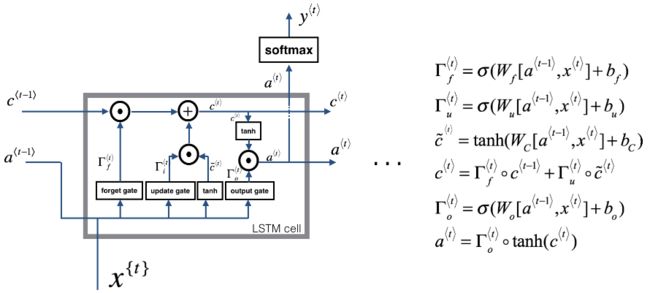
前向传播
由上述的形式方程,很容易得到下面的前向传播公式:
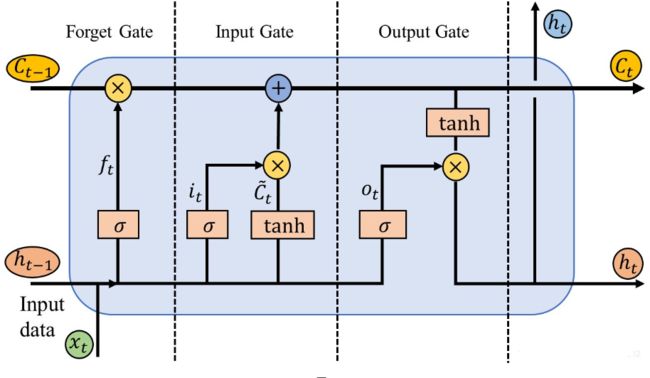
遗忘门。由图片可知,遗忘门的输出依赖三个变量(图1中表示为左下角的两个输入和左上角的一个输入),分别是:上一时刻(t−1)神经元的短时记忆输出![]() 本时刻(t)神经元的输入
本时刻(t)神经元的输入![]()
以及上一时刻(t−1)神经元的长时记忆输出Cell状态![]() ,乘以权重因子后对层数求和即可得到遗忘门的输入值及激活值如下:
,乘以权重因子后对层数求和即可得到遗忘门的输入值及激活值如下:
![]()
输入门。其输出所依赖的变量与遗忘门相同,故同理可得
![]()
![]()
Cell状态。由输入门的t时刻的Cell 状态(长时)方程立即可得
输出门。由遗忘门同理可得
![]()
Cell输出。指激活后的Cell状态(短时记忆),同理可由形式方程一一对应得到,即
反向传播
Cell输出
![]()
注意到这里H HH层时间状态取t+1而K KK层取t,是为了与前向传播式子的意义保持一致,即:隐层Cell状态前向传播需要前一时刻(t−1)的隐层Cell状态,而输出只需与本时刻输入的时刻(t)一致即可,而反向传播正好相反。
再根据带权输入的一般定义(同上,需要根据情况构造定义式,即:H层时刻变化而K层时刻保持不变)
代入得到
![]()
输出门
![]()
Cell状态(长时记忆)
Cell输出
遗忘门
输入门
习题6-5 推导GRU网络中参数的梯度,并分析其避免梯度消失的效果
反向传播
![]()
我们可以进而得到:
![]() 的导数总共和5项相关,即:
的导数总共和5项相关,即:
(5.a)
考虑正向传播的以下公式:
![]()
![]()
![]()
![]()
得到:
(5.a)中的后四项为:
(5.a)可以写为:
提供了关于![]() 的递推关系式,最后一个时间步t=Tx时,只有第一项,所以可以准确求出来,其他时间步则通过传入
的递推关系式,最后一个时间步t=Tx时,只有第一项,所以可以准确求出来,其他时间步则通过传入![]() 的值并递推得到。
的值并递推得到。
以下式子上面已经计算过(只需要把时间步t+1改为t)
结合正向传播的公式:
![]()
![]()
![]()
得到:
![]()
![]()
![]()
所谓防止梯度消失,其实就是防止时间距离过大的两层神经元的参数w之间的联系过少GRU引⼊了重置⻔和更新⻔的概念,从而修改了循环神经⽹络中隐藏状态的计算⽅式。
附加题 6-1P 什么时候应该用GRU? 什么时候用LSTM?
LSTM与GRU的存在都是为了解决简单RNN面临的长期依赖问题
GRU和LSTM的区别在于:
- GRU通过更新门来控制上一时刻的信息传递和当前时刻计算的隐层信息传递。GRU中由于是一个参数进行控制,因而可以选择完全记住上一时刻而不需要当前计算的隐层值,或者完全选择当前计算的隐层值而忽略上一时刻的所有信息,最后一种情况就是无论是上一时刻的信息还是当前计算的隐层值都选择传递到当前时刻隐层值,只是选择的比重不同。而LSTM是由两个参数(遗忘门和输入门)来控制更新的,他们之间并不想GRU中一样只是由一个参数控制,因而在比重选择方面跟GRU有着很大的区别,例如它可以既不选择上一时刻的信息,也不选择当前计算的隐层值信息(输入门拒绝输入,遗忘门选择遗忘)。
- GRU要在上一时刻的隐层信息的基础上乘上一个重置门,而LSTM无需门来对其控制,LSTM必须考虑上一时刻的隐层信息对当前隐层的影响,而GRU则可选择是否考虑上一时刻的隐层信息对当前时刻的影响。
- 一般来说两者效果差不多,性能在很多任务上也不分伯仲。GRU参数更少,收敛更快;数据量很大时,LSTM效果会更好一些,因为LSTM参数也比GRU参数多一些。
附加题 6-2P LSTM BP推导,并用Numpy实现
LSTM的BP推导在上面的题里写过了,这里就不再写了
import numpy as np
def sigmoid(x):
return 1/(1+np.exp(-x))
def softmax(x):
e_x = np.exp(x-np.max(x))# 防溢出
return e_x/e_x.sum(axis=0)
def LSTM_CELL_Forward(xt, h_prev, C_prev, parameters):
"""
Arguments:
xt:时间步“t”处输入的数据 shape(n_x,m)
h_prev:时间步“t-1”的隐藏状态 shape(n_h,m)
C_prev:时间步“t-1”的memory状态 shape(n_h,m)
parameters
Wf 遗忘门的权重矩阵 shape(n_h,n_h+n_x)
bf 遗忘门的偏置 shape(n_h,1)
Wi 输入门的权重矩阵 shape(n_h,n_h+n_x)
bi 输入门的偏置 shape(n_h,1)
Wc 第一个“tanh”的权重矩阵 shape(n_h,n_h+n_x)
bc 第一个“tanh”的偏差 shape(n_h,1)
Wo 输出门的权重矩阵 shape(n_h,n_h+n_x)
bo 输出门的偏置 shape(n_h,1)
Wy 将隐藏状态与输出关联的权重矩阵 shape(n_y,n_h)
by 隐藏状态与输出相关的偏置 shape(n_y,1)
Returns:
h_next -- 下一个隐藏状态 shape(n_h,m)
c_next -- 下一个memory状态 shape(n_h,m)
yt_pred -- 时间步长“t”的预测 shape(n_y,m)
"""
# 获取参数字典中各个参数
Wf = parameters["Wf"]
bf = parameters["bf"]
Wi = parameters["Wi"]
bi = parameters["bi"]
Wc = parameters["Wc"]
bc = parameters["bc"]
Wo = parameters["Wo"]
bo = parameters["bo"]
Wy = parameters["Wy"]
by = parameters["by"]
# 获取 xt 和 Wy 的维度参数
n_x, m = xt.shape
n_y, n_h = Wy.shape
# 拼接 h_prev 和 xt
concat = np.zeros((n_x + n_h, m))
concat[: n_h, :] = h_prev
concat[n_h:, :] = xt
# 计算遗忘门、输入门、记忆细胞候选值、下一时间步的记忆细胞、输出门和下一时间步的隐状态值
ft = sigmoid(np.dot(Wf, concat) + bf)
it = sigmoid(np.dot(Wi, concat) + bi)
cct = np.tanh(np.dot(Wc, concat) + bc)
c_next = ft * c_prev + it * cct
ot = sigmoid(np.dot(Wo, concat) + bo)
h_next = ot * np.tanh(c_next)
# LSTM单元的计算预测
yt_pred = softmax(np.dot(Wy, h_next) + by)
return h_next, c_next, yt_pred
np.random.seed(1)
xt = np.random.randn(3,10)
h_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)
parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
h_next, c_next, yt = LSTM_CELL_Forward(xt, h_prev, c_prev, parameters)
print("a_next[4] = ", h_next[4])
print("a_next.shape = ", c_next.shape)
print("c_next[2] = ", c_next[2])
print("c_next.shape = ", c_next.shape)
print("yt[1] =", yt[1])
print("yt.shape = ", yt.shape)
得到以下结果:
C:\Users\DELL\.conda\envs\pytorch\python.exe C:/Users/DELL/PycharmProjects/pythonProject/CSDN/CSDN/作业10.py
a_next[4] = [-0.66408471 0.0036921 0.02088357 0.22834167 -0.85575339 0.00138482
0.76566531 0.34631421 -0.00215674 0.43827275]
a_next.shape = (5, 10)
c_next[2] = [ 0.63267805 1.00570849 0.35504474 0.20690913 -1.64566718 0.11832942
0.76449811 -0.0981561 -0.74348425 -0.26810932]
c_next.shape = (5, 10)
yt[1] = [0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381
0.00943007 0.12666353 0.39380172 0.07828381]
yt.shape = (2, 10)
进程已结束,退出代码为 0
总结
这次的作业主要写的就是LSTM和GRU网络,我感觉这两个网络差不太多,其实也是,都是为了解决RNN的长程依赖问题,在上面的作业里对GRU和LSTM也进行了推导和比较,推导的过程还是有些难度,很多式子要看好久才能明白,这次的实验也借鉴了很多别人的文章,在接下来的几次实验中要更加注意。
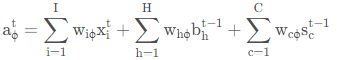
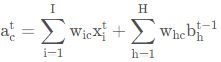
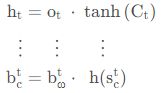


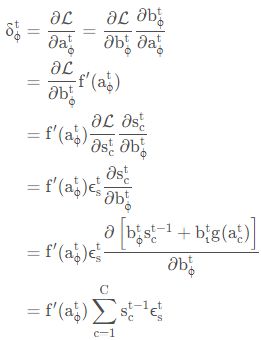
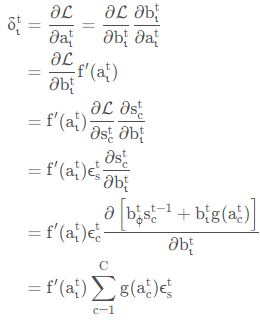

![\frac{\partial L}{\partial W_{cij}}=\sum_{t=1}^{T_x}\frac{\partial L}{\partial \widetilde{c}^{<t>}_i}(1-(\widetilde{c}^{<t>}_i)^2)[\Gamma_r^{<t>}.*c^{<t-1>},x^{<t>}]_j](http://img.e-com-net.com/image/info8/9bac2612cd184176a99af236b804b310.gif)
![\frac{\partial L}{\partial W_{uij}}=\sum_{t=1}^{T_x}\frac{\partial L}{\partial \Gamma^{<t>}_{ui}}\Gamma^{<t>}_{ui}(1-\Gamma^{<t>}_{ui})[c^{<t-1>},x^{<t>}]_j](http://img.e-com-net.com/image/info8/3a810f407c64410f935f674bbb64341b.gif)
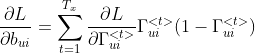
![\frac{\partial L}{\partial W_{rkj}}=\sum_{t=1}^{T_x}\frac{\partial L}{\partial \Gamma^{<t>}_{rk}}\Gamma^{<t>}_{rk}(1-\Gamma^{<t>}_{rk})[c^{<t-1>},x^{<t>}]_j](http://img.e-com-net.com/image/info8/226dbe25a3ce4ba1bdb3b2aa12e86f32.gif)
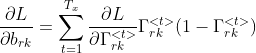
![\frac{\partial L}{\partial W_{cij}}=\sum_{t=1}^{T_x}\frac{\partial L}{\partial c^{<t>}_i}\Gamma_{ui}^{<t>}(1-(\widetilde{c}^{<t>}_i)^2)[\Gamma_r^{<t>}.*c^{<t-1>},x^{<t>}]_j](http://img.e-com-net.com/image/info8/412a1abd6c7f42ef9a28e68134b0bc18.gif)
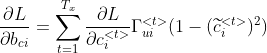
![\frac{\partial L}{\partial W_{uij}}=\sum_{t=1}^{T_x}\frac{\partial L}{\partial c^{<t>}_i}(\widetilde{c}^{<t>}_i-c^{<t-1>}_i)\Gamma^{<t>}_{ui}(1-\Gamma^{<t>}_{ui})[c^{<t-1>},x^{<t>}]_j](http://img.e-com-net.com/image/info8/e4c1293c83104901aa449f9beefc4da6.gif)

![\frac{\partial L}{\partial W_{c}}=\sum_{t=1}^{T_x}\frac{\partial L}{\partial c^{<t>}}.*\Gamma_{u}^{<t>}.*(1-(\widetilde{c}^{<t>})^2)[\Gamma_r^{<t>}.*c^{<t-1>},x^{<t>}]^T](http://img.e-com-net.com/image/info8/1e427d030ca141fb8cc34609bf73e2bd.gif)
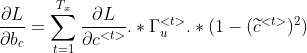
![\frac{\partial L}{\partial W_{u}}=\sum_{t=1}^{T_x}\frac{\partial L}{\partial c^{<t>}}.*(\widetilde{c}^{<t>}-c^{<t-1>}).*\Gamma^{<t>}_{u}.*(1-\Gamma^{<t>}_{u})[c^{<t-1>},x^{<t>}]^T](http://img.e-com-net.com/image/info8/dafde11d88d24098a5d5505ca97e89a5.gif)
