用人话讲明白逻辑回归Logistic regression

今天梳理一下逻辑回归，这个算法由于简单、实用、高效，在业界应用十分广泛。注意咯，这里的“逻辑”是音译“逻辑斯蒂（logistic）”的缩写，并不是说这个算法具有怎样的逻辑性。

前面说过，机器学习算法中的监督式学习可以分为2大类：

• 分类模型：目标变量是分类变量（离散值）；
• 回归模型：目标变量是连续性数值变量。

逻辑回归通常用于解决分类问题，例如，业界经常用它来预测：客户是否会购买某个商品，借款人是否会违约等等。

实际上，“分类”是应用逻辑回归的目的和结果，但中间过程依旧是“回归”。

为什么这么说？

因为通过逻辑回归模型，我们得到的计算结果是0-1之间的连续数字，可以把它称为“可能性”（概率）。对于上述问题，就是：客户购买某个商品的可能性，借款人违约的可能性。

然后，给这个可能性加一个阈值，就成了分类。例如，算出贷款违约的可能性>0.5，将借款人预判为坏客户。

1.从线性回归说起

考虑最简单的情况，即只有一个自变量的情况。比方说广告投入金额x和销售量y的关系，散点图如下，这种情况适用一元线性回归。

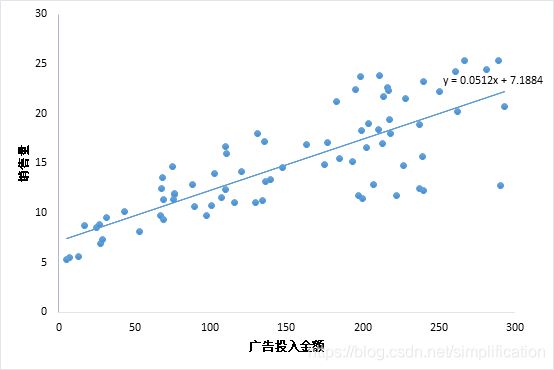
线性回归的介绍文章戳这里：用人话讲明白线性回归LinearRegression

但在许多实际问题中，因变量y是分类型，只取0、1两个值，和x的关系不是上面那样。假设我们有这样一组数据：给不同的用户投放不同金额的广告，记录他们购买广告商品的行为，1代表购买，0代表未购买。

假如此时依旧考虑线性回归模型，得到如下拟合曲线：

线性回归拟合的曲线，看起来和散点毫无关系，似乎没有意义。但我们可以在计算出$\hat{y}$的结果后，加一个限制，即$\hat{y}>0.5$，就认为其属于1这一类，购买了商品，否则认为其不会购买，即：
$$\hat{y}=\{\begin{array}{l}1,f(x)>0.5\\ 0,f(x)\le 0.5\end{array}$$

由于拟合方程为$\hat{y}=0.34\ast x$，那么上面的限制就等价于：
$$\hat{y}=\{\begin{array}{l}1,x>1.47\\ 0,x\le 1.47\end{array}$$

这种形式，非常像单位阶跃函数：
$$y=\{\begin{array}{l}0,z<0\\ 0.5,z=0\\ 1,z>0\end{array}$$

图像如下：

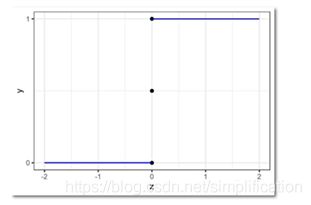
我们发现，把阶跃函数向右平移一下，就可以比较好地拟合上面的散点图呀！但是阶跃函数有个问题，它不是连续函数。

理想的情况，是像线性回归的函数一样，X和Y之间的关系，是用一个单调可导的函数来描述的。

2.sigmond函数

实际上，逻辑回归算法的拟合函数，叫做sigmond函数：
$$f(z)=\frac{1}{1+e^{-z}}$$

函数图像如下（百度图片搜到的图）：

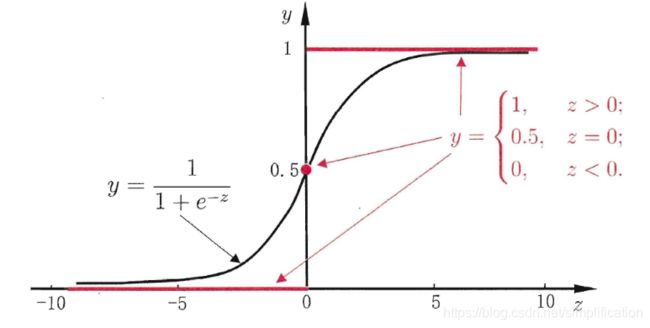
sigmoid函数是一个s形曲线，就像是阶跃函数的温和版，阶跃函数在0和1之间是突然的起跳，而sigmoid有个平滑的过渡。

从图形上看，sigmoid曲线就像是被掰弯捋平后的线性回归直线，将取值范围(−∞,+∞)映射到(0,1) 之间，更适宜表示预测的概率，即事件发生的“可能性” 。

3.推广至多元场景

在用人话讲明白梯度下降Gradient Descent一文中，我们讲了多元线性回归方程的一般形式为：

$$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_p{x}_p$$

可以简写为矩阵形式：
$$\mathbf{Y}=\mathbf{X}\mathbf{\beta }$$

其中，$\mathbf{Y}=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right],\mathbf{X}=\left[\begin{array}{cccc}1& x_{11}& \cdots & x_{1p}\\ 1& x_{21}& \cdots & x_{2p}\\ ⋮& ⋮& & ⋮\\ 1& x_{n1}& \cdots & x_{np}\end{array}\right],\mathbf{\beta }=\left[\begin{array}{c}{\beta }_0\\ {\beta }_1\\ ⋮\\ {\beta }_p\end{array}\right]$

将特征加权求和Xβ（后面不对矩阵向量加粗了，大家应该都能理解）代入sigmond函数中的z，得到$\frac{1}{1+e^{-X\beta }}$，令其为预测为正例的概率P(Y=1)，那么逻辑回归的形式就有了：
$$P(Y=1)=\frac{1}{1+e^{-X\beta }}$$

到目前为止，逻辑函数的构造算是完成了。找到了合适的函数，下面就是求函数中的未知参数向量β了。求解之前，我们需要先理解一个概念——似然性。

4.似然函数

我们常常用概率(Probability) 来描述一个事件发生的可能性。

而似然性(Likelihood) 正好反过来，意思是一个事件实际已经发生了，反推在什么参数条件下，这个事件发生的概率最大。

用数学公式来表达上述意思，就是:

• 已知参数 β 前提下，预测某事件 x 发生的条件概率为$P(x|\beta )$;
• 已知某个已发生的事件 x，未知参数 β 的似然函数为$\mathcal{L}(\beta |x)$；
• 上面两个值相等，即: $\mathcal{L}(\beta |x)=P(x|\beta )$。

一个参数 β 对应一个似然函数的值，当 β 发生变化，$\mathcal{L}(\beta |x)$也会随之变化。当我们在取得某个参数的时候，似然函数的值到达了最大值，说明在这个参数下最有可能发生x事件，即这个参数最合理。

因此，最优β，就是使当前观察到的数据出现的可能性最大的β。

5.最大似然估计

在二分类问题中，y只取0或1，可以组合起来表示y的概率:
$$P(y)=P(y=1{)}^{y}P(y=0{)}^{1-y}$$

我们可以把y=1代入上式验证下：

• 左边是P(y=1)；
• 右边是$P(y=1{)}^{1}P(y=0{)}^0$，也为P(y=1)。

上面的式子，更严谨的写法需要加上特征x和参数β：
$$P(y|x,\beta )=P(y=1|x,\beta {)}^y[1-P(y=1|x,\beta ){]}^{1-y}$$
前面说了，$\frac{1}{1+e^{-x\beta }}$表示的就是P(y=1)，代入上式：

$$P(y|x,\beta )={\left(\frac{1}{1+e^{-x\beta }}\right)}^y{\left(1-\frac{1}{1+e^{-x\beta }}\right)}^{1-y}$$
根据上一小节说的最优β的定义，也就是最大化我们见到的样本数据的概率，即求下式的最大值：
$$\mathcal{L}(\beta )=\prod _{i=1}^{n}P(y_i|x_i,\beta )=\prod _{i=1}^n{\left(\frac{1}{1+e^{-x_i\beta }}\right)}^{y_i}{\left(1-\frac{1}{1+e^{-x_i\beta }}\right)}^{1-y_i}$$

这个式子怎么来的呢？

其实很简单。

前面我们说了，$\mathcal{L}(\beta |x)=P(x|\beta )$，对于某个观测值yi，似然函数的值$\mathcal{L}(\beta |y_i)$，就等于条件概率的值$P(y_i|\beta )$。

另外我们知道，如果事件A与事件B相互独立，那么两者同时发生的概率为P(A)*P(B)。那么我们观测到的y1,y2……yn，他们同时发生的概率就是${\prod }_{i=1}^{n}P(y_i|\beta )$。

因为一系列的xi和yi都是我们实际观测到的数据，式子中未知的只有β。因此，现在问题就变成了求β在取什么值的时候，L(β)能达到最大值。

L(β)是所有观测到的y发生概率的乘积，这种情况求最大值比较麻烦，一般我们会先取对数，将乘积转化成加法。

取对数后，转化成下式：

$$log\mathcal{L}(\beta )=\sum _{i=1}^n\left([y_i\cdot log(\frac{1}{1+e^{-x_i\beta }})]+[(1-y_i)\cdot log(1-\frac{1}{1+e^{-x_i\beta }})]\right)$$

接下来想办法求上式的最大值就可以了，求解前，我们要提一下逻辑回归的损失函数。

6.损失函数

在机器学习领域，总是避免不了谈论损失函数这一概念。损失函数是用于衡量预测值与实际值的偏离程度，即模型预测的错误程度。也就是说，这个值越小，认为模型效果越好，举个极端例子，如果预测完全精确，则损失函数值为0。

在线性回归一文中，我们用到的损失函数是残差平方和SSE：
$$Q=\sum _1^n{\left(y_i-{\hat{y}}_i\right)}^2=\sum _1^n{\left(y_i-x_i\beta \right)}^2$$

这是个凸函数，有全局最优解。

如果逻辑回归也用平方损失，那么就是：
$$Q=\sum _1^n{\left(y_i-\frac{1}{1+e^{-x_i\beta }}\right)}^2$$

很遗憾，这个不是凸函数，不易优化，容易陷入局部最小值，所以逻辑函数用的是别的形式的函数作为损失函数，叫对数损失函数（log loss function）。

这个对数损失，就是上一小节的似然函数取对数后，再取相反数哟：

$$J(\beta )=-log\mathcal{L}(\beta )=-\sum _{i=1}^n\left[y_{i}logP(y_i)+(1-y_i)log(1-P(y_i))\right]$$

这个对数损失函数好理解吗？我还是举个具体例子吧。

用文章开头那个例子，假设我们有一组样本，建立了一个逻辑回归模型P(y=1)=f(x)，其中一个样本A是这样的：

公司花了x=1000元做广告定向投放，某个用户看到广告后购买了，此时实际的y=1，f(x=1000)算出来是0.6，这里有-0.4的偏差，是吗？在逻辑回归中不是用差值计算偏差哦，用的是对数损失，所以它的偏差定义为log0.6（其实也很好理解为什么取对数，因为我们算的是P(y=1)，如果算出来的预测值正好等于1，那么log1=0，偏差为0）。

样本B：x=500，y=0，f(x=500)=0.3，偏差为log(1-0.3)=log0.7。

根据log函数的特性，自变量取值在[0,1]间，log出来是负值，而损失一般用正值表示，所以要取个相反数。因此计算A和B的总损失，就是：-log0.6-log0.7。

之前我们在用人话讲明白梯度下降中解释过梯度下降算法，下面我们就用梯度下降法求损失函数的最小值（也可以用梯度上升算法求似然函数的最大值，这两是等价的）。

7.梯度下降法求解

要开始头疼的公式推导部分了，不要害怕哦，我们还是从最简单的地方开始，非常容易看懂。

首先看，对于sigmoid函数$f(x)=\frac{1}{1+e^{-x}}$，$f^{\prime }(x)$等于多少？

如果你还记得导数表中这2个公式，那就好办了（不记得也没关系，这就给你列出来）：
$$(\frac{1}{x}{)}^{\prime }=-\frac{1}{x^2}$$

$$(e^x{)}^{\prime }=e^x$$

根据上两个公式，推导：
$$f^{\prime }(x)=(\frac{1}{1+e^{-x}}{)}^{\prime }=-\frac{(e^{-x}{)}^{\prime }}{(1+e^{-x}{)}^2}=\frac{e^{-x}}{(1+e^{-x}{)}^2}$$

到这还不算完哦，我们发现$1-f(x)=\frac{e^{-x}}{1+e^{-x}}$，而f’(x)正好可以拆分为$\frac{e^{-x}}{1+e^{-x}}\cdot \frac{1}{1+e^{-x}}$，也就是说：
$$f^{\prime }(x)=f(x)\cdot (1-f(x))$$

当然，现在我们的x是已知的，未知的是β，所以后面是对β求导，记：
$$\frac{1}{1+e^{-x_i\beta }}=f(x_i\beta )$$

把它代入前面我们得到逻辑回归的损失函数：
$$J(\beta )=-\sum _{i=1}^n\left[y_{i}log(f(x_i\beta ))+(1-y_i)log(1-f(x_i\beta ))\right]=-\sum _{i=1}^{n}g({\beta }_i,x_i,y_i)$$

简便起见，先撇开求和号看g(β,x,y)。不过这个g(β,x,y)里面也挺复杂的，我们再把里面的$f(x_i\beta )$挑出来，单独先看它对β向量中的某个βj求偏导是什么样。

根据上面的求导公式，有：
$$\frac{\partial f(x_i\beta )}{\partial {\beta }_j}=f(x_i\beta )\cdot (1-f(x_i\beta ))\cdot x_{ij}$$

注意咯，这个xi实际上指的是第i个样本的特征向量，即$(1,x_{i1},...,x_{ip})$，其中只有xij会和βj相乘，因此求导后整个xi只剩xij了。

理解了前面说的，下面的化简就轻而易举：
$$\begin{array}{rl}\frac{\partial g({\beta }_i,x_i,y_i)}{\partial {\beta }_j}& =y_i\frac{1}{f(x_i\beta )}\frac{\partial f(x_i\beta )}{\partial {\beta }_j}-\left(1-y_i\right)\frac{1}{1-f(x_i\beta )}\frac{\partial f(x_i\beta )}{\partial {\beta }_j}\\ & =\left(\frac{y_i}{f(x_i\beta )}-\frac{1-y_i}{1-f(x_i\beta )}\right)\cdot \frac{\partial f(x_i\beta )}{\partial {\beta }_j}\\ & =\left(\frac{y_i}{f(x_i\beta )}-\frac{1-y_i}{1-f(x_i\beta )}\right)\cdot f(x_i\beta )\cdot (1-f(x_i\beta ))\cdot x_{ij}\\ & =\left[y_i(1-f(x_i\beta ))-(1-y_i)f(x_i\beta )\right]\cdot x_{ij}\\ & =\left(y_i-f(x_i\beta )\right)\cdot x_{ij}\end{array}$$

加上求和号：
$$\frac{\partial J(\beta )}{\partial {\beta }_j}=-\sum _{i=1}^n\left(y_i-f(x_i\beta )\right)\cdot x_{ij}=\sum _{i=1}^n\left(\frac{1}{1+e^{-x_i\beta }}-y_i\right)\cdot x_{ij}$$

有了偏导，也就有了梯度G，即偏导函数组成的向量。

梯度下降算法过程：

1. 初始化$\beta$向量的值，即${\Theta }_0$，将其代入G得到当前位置的梯度；
2. 用步长$\alpha$乘以当前梯度，得到从当前位置下降的距离；
3. 更新${\Theta }_1$，其更新表达式为${\Theta }_1={\Theta }_0-\alpha G$；
4. 重复以上步骤，直到更新到某个${\Theta }_k$，达到停止条件，这个${\Theta }_k$就是我们求解的参数向量。

8.结尾

文章写到这里就结束了，其实逻辑回归还有很多值得深入学习和讨论的，但是“讲人话”系列的定位就是个入门，本人水平也有限，所以本篇不再往后写了。

主要一篇文章写起来蛮累……其他都还好，就是打公式挺麻烦，还挺费时间>.<

最后，欢迎各位一起学习讨论啊~