机器学习算法理论与实践——Logistic回归

一、基本思想

  Logistic回归是一种广义线性回归模型，解决的是分类问题。其思想是运用对数几率函数将线性回归$(-\infty ,+\infty )$的实数预测值转化为$(0,1)$之间的值，并视该值为正反例的概率对类别进行预测。

二、数学推导

1.二分类

  对数几率函数(logistic function)
$$y=\frac{1}{1+e^{-z}}$$
其中$z\in (-\infty ,+\infty )$，$y\in \{0,1\}$，$z=w^{T}x+b$表示线性回归模型。经过对数变换可得
$$\ln \frac{y}{1-y}=w^{T}x+b$$
  $y$代表正例的可能性，$1-y$代表反例的可能性，$\frac{y}{1-y}$称为几率(odds)，$\ln (\frac{y}{1-y})$称为对数几率(log odds，亦称logit)。所以这个模型也叫对数几率回归模型(Logistic Regression)。
  将$y$视为后验概率估计$p(y=1|x)$，$1-y$视为$p(y=0|x)$，则有
$$\begin{array}{l}p(y=1|x)=\frac{e^{w^{T}x+b}}{1+e^{w^{T}x+b}}\\ \\ p(y=0|x)=\frac{1}{1+e^{w^{T}x+b}}\end{array}$$
  通过极大似然法来估计$w$和$b$，即令每个样本属于其真实标记的概率越大越好。
$$\ell (w,b)=\sum _{i=1}^m\ln p(y_i|x_i;w,b)$$
  令$\beta =(w;b),\hat{x}=(x;1)$，则$w^{T}x+b={\beta }^T\hat{x}$。令$p_1(\hat{x};\beta )=p(y=1|\hat{x};\beta ),p_0(\hat{x};\beta )=p(y=0|\hat{x};\beta )$，则
$$\begin{array}{l}\ln p(y_i|x_i;w,b)=\ln (y_i{p}_1({\hat{x}}_i;\beta )+(1-y_i)p_0({\hat{x}}_i;\beta ))\\ \\ =\ln (\frac{y_i{e}^{{\beta }^T\hat{x}}}{1+e^{{\beta }^T\hat{x}}}+\frac{1-y_i}{1+e^{{\beta }^T\hat{x}}})\\ \\ =\ln (y_i{e}^{{\beta }^T{\hat{x}}_i}+1-y_i)-\ln (1+e^{{\beta }^T{\hat{x}}_i})\\ \\ =\{\begin{array}{l}-\ln (1+e^{{\beta }^T{\hat{x}}_i}),y_i=0\\ {\beta }^T{\hat{x}}_i-\ln (1+e^{{\beta }^T{\hat{x}}_i}),y_i=1\end{array}\end{array}$$
所以就变成了最小化
$$\ell (\beta )=\sum _{i=1}^m(-y_i{\beta }^T{\hat{x}}_i+\ln (1+e^{{\beta }^T{\hat{x}}_i}))$$
$\ell (\beta )$是关于$\beta$的高阶可导连续凸函数，根据凸优化理论，梯度下降法、牛顿法等可求得其最优解
$${\beta }^{\ast }=\arg \underset{\beta }{\min }\ell (\beta )$$
以梯度下降法为例，第$t+1$轮的更新公式
$${\beta }_{t+1}={\beta }_t-\alpha \frac{\partial \ell (\beta )}{\partial {\beta }_t}$$
迭代直到阈值即可求出$\beta$的数值解。

2.多分类

  多分类学习的思想是"拆解法"，将多分类任务拆为若干个二分类任务求解。

（1）一对一

  One vs. One，简称OvO。
  给定数据集$D=\{(x_i,y_i){\}}_{i=1}^m,y_i\in \{C_1,C_2,\dots ,C_N\}$，将这N个类别两两配对，从而产生N(N-1)/2个二分类任务，训练得到N(N-1)/2个分类器。将新样本同时提交给所有分类器，将得到N(N-1)/2个分类结果，最终结果可投票产生：即把被预测得最多的类别作为最终分类结果。

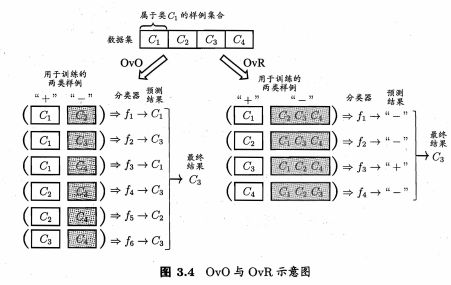
（2）一对其余

  One vs. Rest，简称OvR。
  每次将一个类的样例作为正例、所有其他类的样例作为反例，可训练得到N个分类器。对于新样本，若仅有一个分类器预测为正类，则最终分类结果为正类；若有多个分类器预测为正类，则通常考虑各分类器的预测置信度，选择置信度最大的类别标记作为分类结果。

（3）多对多

  Many vs. Many，简称MvM。
  每次将若干个类作为正类，若干个其他类作为反类，但正、反类构造必须有特殊的设计，最常用的是"纠错输出码"(Error Correcting Output Codes，简称ECOC)。

  ECOC分两步：

1. 编码：对N个分类做M次划分，每次划分将一部分类别划为正类，一部分划为反类，这样一共产生M个训练集，可训练出M个分类器。
2. 解码：M个分类器分别对测试样本进行预测，预测结果组成一个编码，将此预测编码与每个类别的编码进行比较，距离最小的类别作为最终预测结果。

  类别划分通过"编码矩阵"指定，编码矩阵常用二元码和三元码。二元码将每个类别指定为正类和负类，三元码还有一个停用类，表示该学习器不使用这一类的样本进行训练。

比如上图中，数据集有4(N)个分类，第一步编码做了5(M)次划分，训练出5个分类器$f_1,f_2,\dots ,f_5$，训练$f_1$的数据集是将第2类划分为正类，第1、3、4类划分为负类。5个分类器分别对测试样本作出的预测组成了预测编码（-1，-1，+1，-1，+1），这个预测编码再与每个类别的编码计算距离，比如第1类的编码是（-1，+1，-1，+1，+1），预测编码与第1类编码的欧氏距离就是$\sqrt{(-1-(-1){)}^2+(-1-1{)}^2+(1-(-1){)}^2+(-1-1{)}^2+(1-1{)}^2}=2\sqrt{3}$。

三、sklearn包中的LogisticRegression

  sklearn中关于实现Logistic回归的类是sklearn.linear_model.LogisticRegression，官方文档：https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression
  下面是该类各参数、属性和方法的介绍，基本翻译自官方文档：

sklearn.linear_model.LogisticRegression(penalty=‘l2’, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver=‘liblinear’, max_iter=100, multi_class=‘ovr’, verbose=0, warm_start=False, n_jobs=None, l1_ratio=None)

1.参数解释

1. penalty：字符串，可选参数。指定正则化惩罚项使用的范数。可选方法有
   (1) ‘l1’：L1范数，若特征非常多，希望一些不重要的特征系数为零，可使用L1范数。
   (2) ‘l2’(默认)：L2范数，‘newton-cg’、‘sag’、‘lbfgs’ 方法仅支持L2范数。
   (3) ‘elasticnet’：弹性网络，仅支持 ‘saga’ 方法。
   (4) ‘none’：不设置正则化项，不支持 ‘liblinear’ 方法。
2. dual：布尔值，可选参数，默认为False。选择原始函数还是对偶函数。对偶函数仅在penalty为’l2’、solver为’liblinear’时才可使用，如果样本数大于特征数则推荐使用原始函数。
3. tol：浮点数，可选参数，默认值为0.0001。模型迭代收敛的阈值。
4. C：浮点数，可选参数，默认值为1.0。正则化强度的倒数。值越小，正则化越强，该值必须为正数。
5. fit_intercept：布尔值，可选参数，默认为True。是否添加截距项。相当于在X数据集上人为添加常数列1，用于计算截距项。
6. intercept_scaling：浮点数，可选参数，默认为1。当solver为’liblinear’且fit_intercept为True时生效，此时数据集X变为$[X,intercept\_scaling]$，而截距项变为intercept_scaling * synthetic_feature_weight$（w^T[X,intercept\_scaling]）$。注意人为增加的特征权重synthetic_feature_weight，也就是系数w增加一行，同样受正则化项的影响，为了减小该影响，必须增加intercept_scaling。
7. class_weight：可选参数，指定因变量各类别的权重。
   (1) 字典：形如{class_label: weight}
   (2) ‘balanced’：每个分类的权重与实际样本中的比例成反比
   (3) None(默认)：每个类别的权重都一样
   如果fit方法中sample_weight指定了，则类别权重会跟样本权重(sample_weight)相乘。
8. random_state：可选参数，设定随机种子，solver为’sag’或’liblinear’时可用。根据不同参数值，random_state有几种情况
   (1) 整数：random_state是随机数生成器使用的种子
   (2) RandomState实例：random_state是随机数生成器
   (3) None(默认)：随机数生成器是np.random使用的RandomState实例
9. solver：字符串，可选参数，默认值为’liblinear’。求解目标函数最优化的算法。可用方法有’newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’ 。
   (1) ‘lbfgs’：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
   (2) ‘newton-cg’：共轭梯度法，也是牛顿家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
   (3) ‘liblinear’：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。
   (4) ‘sag’：即随机平均梯度下降，是梯度下降法的变种，和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。
   (5) ‘saga’：线性收敛的随机优化算法。
   使用时有如下规则：
   $\bullet$ 小规模数据集，适合’liblinear’；大规模数据集，'sag’和’saga’更快。
   $\bullet$ 多分类问题，只有 ‘lbfgs’ , ‘newton-cg’, ‘sag’, ‘saga’ 可以处理多项损失，‘liblinear’ 只能处理 一对其余（One vs. Rest）的情况。
   $\bullet$ ‘lbfgs’ , ‘newton-cg’, ‘sag’, ‘saga’ 可使用L2范数的惩罚项或者无惩罚项。
   $\bullet$ 'liblinear’和’saga’可使用L1范数的惩罚项。
   $\bullet$ 'saga’可使用’elasticnet’惩罚项。
   $\bullet$ 'liblinear’不支持无惩罚项。
   注意 ‘sag’ 和 ‘saga’ 能够快速收敛需要各类特征值比例大体一致。
10. max_iter：整数，可选参数，默认值为100。指定模型求解最大的迭代次数。
11. multi_class：字符串，可选参数，默认值为’ovr’。指定多分类的解决方法。
    (1) ‘ovr’(默认)：one vs. rest，一对其余（每次将一个类的样例作为正例、所有其他类的样例作为反例）。
    (2) ‘multinomial’：many vs many，多对多（每次将若干个类作为正类，若干个其他类作为反类），solver为’liblinear’时不可用。
    (3) ‘auto’：二分类时自动选择’ovr’；slover为’liblinear’或其他情况自动选择’multinomial’。
12. verbose：整数，可选参数，默认值为0。日志冗长度，对于solver为‘liblinear’和‘lbfgs’将设置为任何正数以表示详细程度。
13. warm_start：布尔值，可选参数，默认值为False。如果设置为True，则会使用上一次的结果作为初始值，否则会清除上一次结果。
14. n_jobs：整数或None，可选参数，默认值为None。如果multi_class为’ovr’时指定CPU核心使用数量。如果solver为’liblinear’，则该参数无论multi_class是否设置都会忽略。None为至少使用1个CPU核心，-1为使用全部CPU核心。
15. l1_ratio：浮点数或None，可选参数，默认值为None。Elastic-Net混合参数，0<= l1_ratio <=1，仅当penalty为’elasticnet’时可用。l1_ratio=0时等同于penalty使用’l2’，l1_ratio=1时等同于penalty使用’l1’，0< l1_ratio <1时是L1范数和L2范数的结合。

2.属性解释

1. classes_：数组，shape(分类数,)。分类类别的列表。
2. coef_：数组，shape (1, 特征数,) or shape(分类数, 特征数)。系数矩阵。二分类时为shape (1, 特征数,)；多分类时为shape(分类数, 特征数)。
3. intercept_：数组，shape (1, ) or shape(分类数,) 。截距。
4. n_iter_：数组，shape (分类数,) or shape(1,)。迭代次数。

3.方法解释

1. decision_function(self, X)：
   预测置信度分数。置信度分数是样本到（分类）超平面的带符号的距离。
   参数：
   $\bullet$ X: shape(样本数, 特征数)
   返回值：
   $\bullet$ 数组，二分类——shape(样本数,)，多分类——shape(样本数, 分类数)
2. densify(self)：
   将系数矩阵转化为稠密形式。仅在事先做过稀疏化的模型上使用。
3. fit(self, X, y, sample_weight=None)：
   训练模型。
   参数：
   $\bullet$ X：shape(样本数, 特征数)，自变量
   $\bullet$ y：shape(样本数,)，因变量
   $\bullet$ sample_weight：shape(样本数, )，可选参数。每个样本的权重，如果不设置，则每个样本都被赋予一个单位权重。
   返回值：
   $\bullet$ 实例对象
4. get_params(self, deep=True)：
   以字典返回LDA模型的参数值，比如solver等。参数deep默认为True，还会返回包含的子模型的参数值。
5. predict(self, X)：
   根据模型的训练，返回预测值。
   参数：
   $\bullet$ X: shape(样本数, 特征数)
   返回值：
   $\bullet$ 数组，shape [样本数]
6. predict_log_proba(self, X)：
   返回X中每一个样本预测为各个分类的对数概率
   参数：
   $\bullet$ X: shape(样本数, 特征数)
   返回值：
   $\bullet$ 数组，shape(样本数, 分类数)
7. predict_proba(self, X)：
   返回X中每一个样本预测为各个分类的概率
   参数：
   $\bullet$ X: shape(样本数, 特征数)
   返回值：
   $\bullet$ 数组，shape(样本数, 分类数)
8. score(self, X, y, sample_weight=None)：
   根据给定的测试数据X和分类标签y返回预测正确的平均准确率。可以用于性能度量，返回模型的准确率，参数为x_test，y_test。
   $\bullet$ 参数：X,y,sample_weight
   $\bullet$ 返回值：浮点数
9. set_params(self, **params)：
   设定参数。
10. sparsify(self)：
    将系数矩阵转化为稀疏形式。L1正则化模型更适合稀疏化，截距项intercept_不会转化。（注意系数矩阵中0超过50%时用此方法才有效率，否则会占用很多内存）

  注意sklearn.linear_model.LogisticRegression()中提供了正则化惩罚项的参数，正则化是避免模型训练过拟合的重要手段，即在目标函数中加入一个正则化项
$$\underset{f}{\min }\Omega (f)+C\sum _{i=1}^m\ell (f(x_i),y_i)$$
其中$\Omega (f)$称为"结构风险"，用于描述模型$f$的某些性质；${\sum }_{i=1}^m\ell (f(x_i),y_i)$称为"经验风险"，用于描述模型与训练数据的契合程度(也就是本模型中的$\ell (\beta )$)；$C$用于对二者进行折中。正则化可理解为对不希望得到的结果施以惩罚，降低过拟合的风险。$\Omega (f)$称为正则化项，$C$为正则化常数。$L_p$范数是常用的正则化项（$||x|{|}_p=\sqrt[p]{{\sum }_{i=1}^n|x_i{|}^p}$）。

四、实例

1.数据来源

  Logistic回归在信用违约方面的运用是比较普遍的，信贷评分卡的基础模型就是Logistic回归模型。本例数据来源于机器学习竞赛平台Kaggle，一个关于信用违约的数据。数据地址：https://www.kaggle.com/singh001avinash/default-credit-card

2.数据概况

  数据一共10000个样例，3个字段。分类字段为default，一共分为了两类。数据集无缺失值，无错误值。字段及解释如下

  该数据集特征数较少，仅作为Logistic回归的示范。 其中student字段取值为"Yes"和"No"，需要先做哑变量处理。

3.代码实现

import pandas as pd
import numpy as np
import os
from sklearn.linear_model import LogisticRegression
from sklearn import model_selection
from sklearn import metrics
import matplotlib.pyplot as plt

# 读取数据
path = os.path.join(os.getcwd(), 'credit_default.csv')
data = pd.read_csv(path)
# 设置正例和负例，便于后面画ROC曲线
data.default = data.default.map({'No': 0, 'Yes': 1})

# 哑变量处理
dummies = pd.get_dummies(data.student, prefix='student')
data.drop('student', axis=1, inplace=True)
data_new = pd.concat([data, dummies], axis=1)

x = data_new[data_new.columns[1:]]
y = data_new[data_new.columns[0]]  # 本例第一列为分类标签
# 拆分为训练集和测试集
x_train, x_test, y_train, y_test = model_selection.train_test_split(x, y, test_size=0.25)

# 训练模型
lr = LogisticRegression()
lr.fit(x_train, y_train)

# 模型评估
# 准确率
print('模型准确率：', lr.score(x_test, y_test))
# ROC曲线
# y_score为模型预测正例的概率
y_score = lr.predict_proba(x_test)[:, 1]
# 计算不同阈值下，fpr和tpr的组合之，fpr表示1-Specificity，tpr表示Sensitivity
fpr, tpr, threshold = metrics.roc_curve(y_test, y_score)
# 计算AUC
roc_auc = metrics.auc(fpr, tpr)
# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha=0.5, edgecolor='black')
# 添加ROC曲线的轮廓
plt.plot(fpr, tpr, color='black', lw=1)
# 添加对角线作为参考线
plt.plot([0, 1], [0, 1], color='red', linestyle='--')
plt.text(0.5, 0.3, 'ROC curve (area=%0.2f)' % roc_auc)
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
plt.show()

  最终得到模型的准确率为97%，但是AUC并不大。


参考文献：
[1]周志华.《机器学习》.清华大学出版社,2016-1
[2]https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression