【蚁群系统】解决TSP旅行商问题（matlab实现）

1. 蚁群系统（Ant Colony System）(ACS)

1997年，蚁群算法的创始人Dorigo在“Ant colony system: a cooperative learning approach to the traveling salesman problem”一文中提出了一种具有全新机制的ACO算法——蚁群系统（Ant Colony System，ACS），进一步提高了ACO算法的性能。

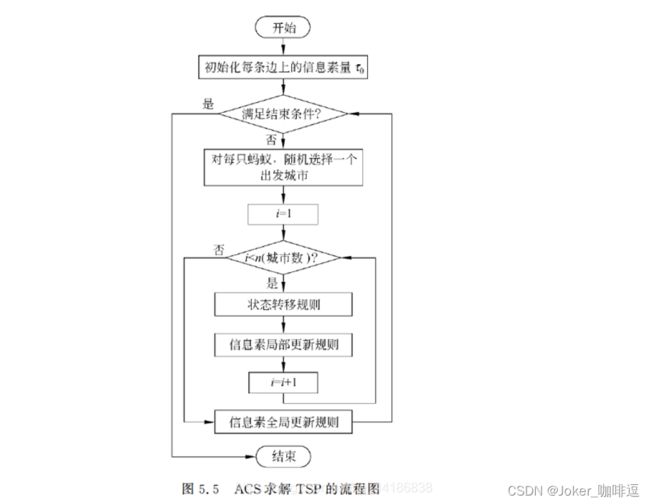
（1）使用一种伪随机比例规则（pseudorandom proportional）选择下城市节点，建立开发当前路径与探索新路径之间的平衡。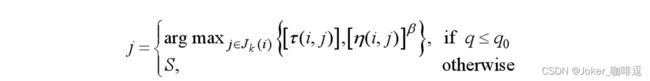

• q0是一个[0, 1]区间内的参数，当产生的随机数q≤q0时，蚂蚁直接选择使启发式信息与信息素量的指数乘积最大的下城市节点，我们通常称之为开发（exploitation）；反之，当产生的随机数q>q0时ACS将和各种AS算法一样使用轮盘赌选择策略，我们称之为偏向探索（bias exploration）。通过调整q0，我们能有效调节“开发”与“探索”之间的平衡，以决定算法是集中开发最优路径附近的区域，还是探索其它的区域。

（2）使用信息素全局更新规则，每轮迭代中所有蚂蚁都已构建完路径后，在属于至今最优路径的边上蒸发和释放信息素。

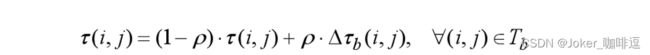
• 不论是信息素的蒸发还是释放，都只在属于至今最优路径的边上进行，这里与AS有很大的区别。因为AS算法将信息素的更新应用到了系统的所有边上，信息素更新的计算复杂度为O(n^2），而ACS算法的信息素更新计算复杂度降低为O（n）。参数ρ 代表信息素蒸发的速率，新增加的信息素 被乘上系数ρ 后，更新后的信息素浓度被控制在旧信息素量与新释放的信息素量之间，用一种隐含的又更简单的方式实现了MMAS算法中对信息素量取值范围的限制。

（3）引入信息素局部更新规则，在路径构建过程中，对每一只蚂蚁，每当其经过一条边(i, j)时，它将立刻对这条边进行信息素的更新。

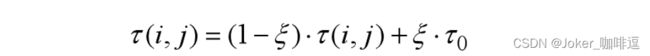
• 信息素局部更新规则作用于某条边上会使得这条边被其他蚂蚁选中的概率减少。这种机制大大增加了算法的探索能力，后续蚂蚁倾向于探索未被使用过的边，有效地避免了算法进入停滞状态。
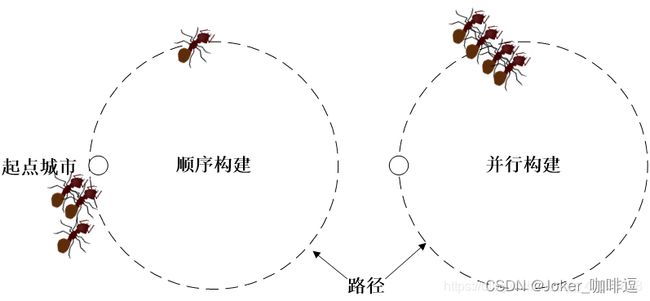
• 顺序构建和并行构建。顺序构建是指当一只蚂蚁完成一轮完整的构建并返回到初始城市之后，下一只蚂蚁才开始构建；并行构建是指所有蚂蚁同时开始构建，每次所有蚂蚁各走一步（从当前城市移动到下一个城市）。对于ACS，要注意到两种路径构建方式会造成算法行为的区别。在ACS中通常我们选择让所有蚂蚁并行地工作。
  

总结：

• ACS解决了基本蚁群算法在构造解过程汇总，随机选择策略造成的算法进化速度慢的缺点。该算法在每一次循环中仅让最短路径上的信息量作更新，且以较大的概率让信息量最大的路径被选中，充分利用学习机制，强化最优信息的反馈。ACS的核心思想是：蚂蚁在寻找最佳路径的过程中只能使用局部信息，即采用局部信息对路径上的信息量进行调整；在所有进行寻优的蚂蚁结束路径的搜索后，路径上的信息量会再一次调整，这次采用的是全局信息，而且只对过程中发现的最好路径上的信息量进行加强。
  ACS模型与AS模型的主要区别有三点：
  （1）蚂蚁的状态转移规则不同
  （2）全局更新规则不同
  （3）新增了对各条路径信息量调整的局部更新规则

2. 旅行商问题

假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。这就是TSP，属于NPC问题。

3. 蚁群系统解决TSP问题（Matlab）

function [R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=ACS(NC_max,m,Alpha,Beta,Rho,Q)
clear all;
close all;
clc;
% 重要参数说明：
%  R_best   各代最佳路线
%  L_best   各代最佳路线的长度

%% 第一步：变量初始化
C=[5.294,1.558;4.286,3.622;4.719,2.774;4.185,2.230;0.915,3.821;4.771,6.041;1.524,2.871;3.447,2.111;3.718,3.665;2.649,2.556];%n个城市的坐标，n×2的矩阵
n=size(C,1);     % 表示城市个数n=10
D=zeros(n,n);		% D表示完全图的赋权邻接矩阵,产生n*n的值全为0的矩阵
for i=1:n
    for j=1:n
        D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
    end
end

m = 50;          % 蚂蚁个数 50
q0=0.9;          % 参数q0
NC_max = 100;    % 最大迭代次数 100
Alpha = 2;       % 表征信息素重要程度的参数2
Beta = 4;        % 表征启发式因子重要程度的参数4
Rho = 0.1;       % 信息素蒸发系数0.1
Q = 0.01;        % 信息素增加强度系数 0.01
Eta=1./D;        % Eta为启发因子,为距离的倒数
Lnn=10;
TauStart=(1/(n*Lnn)).*ones(n,n);       %TauStart为信息素有个初始值    Tau：产生10*10行矩阵
Tabu=zeros(m,n);            % 存储并记录路径    Tabu：50*10矩阵
NC=1;                       % 迭代计数器
R_best=zeros(NC_max,n);     % 各代最佳路线  100*10
L_best=inf.*ones(NC_max,1); % 各代最佳路线的长度 100*1
L_ave=zeros(NC_max,1);      % 各代路线的平均长度 100*1

%% 第二步： 将m=50只蚂蚁放到n=10个城市上
while NC<=NC_max           
    Randpos=[];
	Tau=TauStart;
    for i=1:(ceil(m/n))     % m为50，n为10
        Randpos=[Randpos,randperm(n)];  % 将每只蚂蚁放到随机的城市
    end

    Tabu(:,1)=(Randpos(1,:)); % 初始化禁忌表中第一个元素  矩阵的第一行赋值给另外一个矩阵的第一列
   
    %% 第三步：对每只蚂蚁按概率函数选择下一座城市，完成各自的周游
    for j=2:n
        for i=1:m
			% 选择下一个访问的城市
            visited=Tabu(i,1:(j-1));		% 在访问第j个城市的时候，第i个蚂蚁访问过的城市, visited也是矩阵
            unvisited=zeros(1,(n-j+1));				% 待访问的城市      
            P=unvisited;						    % 待访问城市的选择概率分布   J、P都是一行值为0的矩阵
            Jc=1;

            % 找出未访问的城市  
            for k=1:n                       
                if length(find(visited==k))==0
                    unvisited(Jc)=k;
                    Jc=Jc+1;
                end
            end
            %  计算待选择城市的概率
			for k=1:length(unvisited)       % Tau(visited(end),unvisited(k))访问过的城市的最后一个与所有未访问的城市之间的信息素
				P(k)=(Tau(visited(end),unvisited(k))^Alpha)*(Eta(visited(end),unvisited(k))^Beta);
            end
            % 状态转移规则
			q=rand();
			if q<=q0  
				Select=find(P==max(P));
            else   % 轮盘赌
				P=P/(sum(P));
				Pcum=cumsum(P);
				Select=find(Pcum>=rand);
            end

            % 添加到禁忌表
            to_visit=unvisited(Select(1));
            Tabu(i,j)=to_visit;
        end
		
		% 信息素局部更新
		Tau=(1-Rho).*Tau+Rho.*TauStart;	
    end
	
    if NC>=2
        Tabu(1,:)=R_best(NC-1,:);   % 上一代最短路径作为本代第一条路径
    end
   
    %% 第四步：记录本次迭代最佳路线
    L=zeros(m,1);
    for i=1:m
        R=Tabu(i,:);
        for j=1:(n-1)
            L(i)=L(i)+D(R(j),R(j+1));   % 要走一周回到原来的地点  
        end
        L(i)=L(i)+D(R(1),R(n));
    end
	

    L_best(NC)=min(L);                  % 记录每一代中路径的最短值
    pos=find(L==L_best(NC));
    R_best(NC,:)=Tabu(pos(1),:);        % 最优的路径
    L_ave(NC)=mean(L);                  % 每一代中平均路径长度
    NC=NC+1;
   
    %% 第五步：更新全局信息素（增加了全局最短路径的信息素）
    Delta_Tau=zeros(n,n);
	
    for j=1:(n-1)
        Delta_Tau(Tabu(pos(1),j),Tabu(pos(1),j+1))=Delta_Tau(Tabu(pos(1),j),Tabu(pos(1),j+1))+1/min(L);
    end
    Delta_Tau(Tabu(pos(1),n),Tabu(pos(1),1))=Delta_Tau(Tabu(pos(1),n),Tabu(pos(1),1))+1/min(L);
    
	
    Tau=(1-Rho).*Tau+Rho.*Delta_Tau;    % 更新路径上的信息素含量
   
    %%第六步：禁忌表清零
    Tabu=zeros(m,n);
end

%% 第七步：输出结果
Pos=find(L_best==min(L_best));
Shortest_Route=R_best(Pos(1),:);
Shortest_Length=L_best(Pos(1));
% 画图
subplot(1,2,1)
DrawRoute(C,Shortest_Route)
subplot(1,2,2)
plot(L_best,'b')
hold on
plot(L_ave,'r')
title('平均距离和最短距离')

disp('最短距离为:')
disp(min(L_best))

num=find(min(L_best)==L_best)
disp('最短路径是:')
disp(R_best(num(1),:))


%% 画路线图
function DrawRoute(C,R)

% C    节点坐标，由一个N×2的矩阵存储
% R    路线

N=length(R);
scatter(C(:,1),C(:,2));
hold on
plot([C(R(1),1),C(R(N),1)],[C(R(1),2),C(R(N),2)],'g')
hold on
for ii=2:N
    plot([C(R(ii-1),1),C(R(ii),1)],[C(R(ii-1),2),C(R(ii),2)],'g')
    hold on
end
title('旅行商问题优化结果');