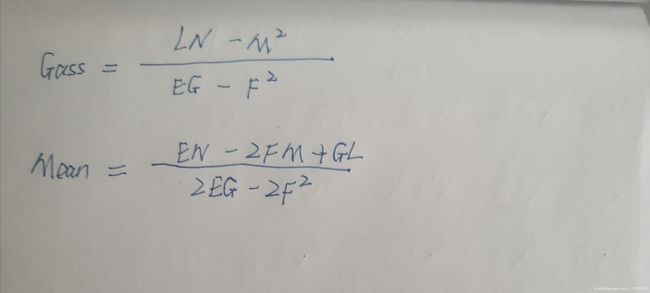（曲率系列4：）基于点拟合二次曲面并求曲率
现实世界中的一切，都可以用二次曲面表示，那么如何拟合二次曲面呢？
一、定义
二次曲面是在三维坐标系(x、y、z)下三元二次代数方程对应的所有图形的统称。在欧氏三维空间里坐标x,y,z之间的二次方程（系数为实数，且二次项系数不全为零）所表示的曲面。
空间二次曲面的一般形式方程为：
二、分类：
二次曲面有12种：
(1)圆柱面(Cyindrical surface)
(2)椭圆柱面(Elliptic cylinder)
(3)双曲柱面(Hyperbolic cylinder)
(4)抛物柱面(Parabolic cylinder)
(5)圆锥面(Conical surface)
(6)椭圆锥面(Elliptic cone)
(7)球面(Sphherical surface)
(8)椭球面(Ellipsoid)
(9)椭圆抛物面(Elliptic paraboloid)
(10)单叶双曲面(Hyperboloid of one sheet)
(11)双叶双曲面(Hyperboloid of two sheets)
(12)双曲抛物面(马鞍面)(Hyperbolic paraboloid)
最常见的二次曲面是球面和直圆柱面及直圆锥面。此外，二次曲面还包括椭球面、双曲面（又分为单叶双曲面和双叶双曲面）和抛物面（又分为椭圆抛物面和双曲抛物面，后者又称马鞍面）。当表示二次曲面的一个方程，能分解为两个一次方程的乘积时，这个二次曲面就退化成两个或相交或平行或重合的平面。
三、空间二次曲面的标准表达式：
这里具体可以参考这个文章：二次曲面方程三维标准化及其图形实质
空间二次曲面的标准表达式化为含abcdef6个参数的表达式。
举例：如下以椭球面为例子进行二次曲面拟合：
一下推导使用最小二乘：由于它的原理直观，算法简单，收敛性能好，且不要求先验的统计知识，因而被广泛应用。最小二乘法是在1795年由大数学家高斯(C.F.Gauss)研究天体运动轨道问题提出的，它的基本原理是实际观测值与模型计算值的误差的平方和最小原理，由此而得名“最小二乘”法。应该注意的是最小二乘法是一种思想，由它衍生出来的公式可以有很多种。本次的空间二次数据拟合算法的推导利用的也是最小二乘法，不同的是本次是先估计参数a,b,c,d,e,f，然后间接的得到参数x0, y0, z0, A, B, C，这样做给公式推导带来了很大的方便，而且结果与直接推导的完全一样。参考链接：https://blog.csdn.net/hj199404182515/article/details/53462512
https://blog.csdn.net/HJ199404182515/article/details/59480954
对于有N个三维椭球面样本对其进行椭球面拟合，我们只需要对参数a,b,c,d,e,f进行估计，从而就可以得到x0, y0, z0, A, B, C。那么怎么利用样本去估计这些参数呢？这实际上就是模型参数估计的内容，模型参数估计有很多种方法，其中最基本的方法就是最小二乘法(Least Squares Method)。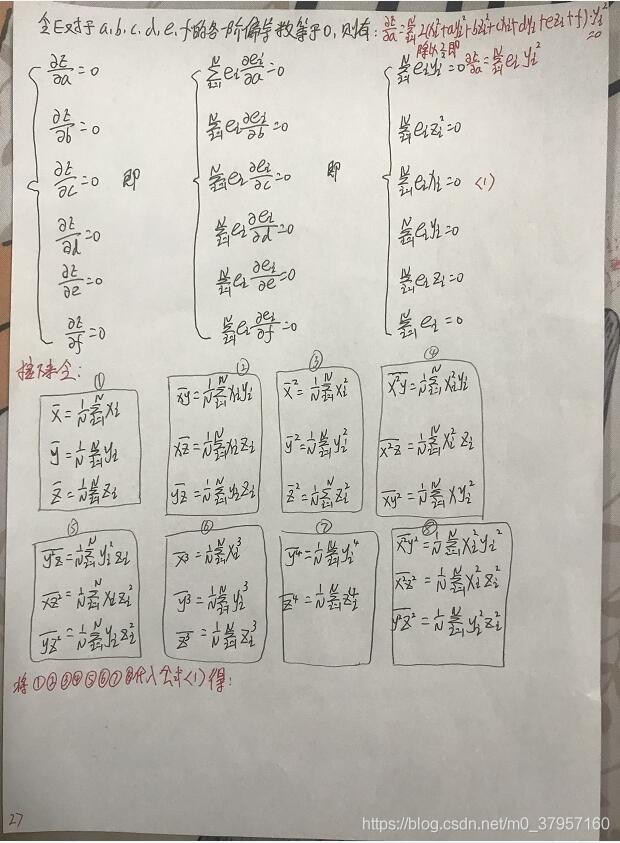
之后求uv，第一基本量、第二基本量进而进行曲率求解。。。。。。。。。。。。。。（有空接着推导）
参考连接：http://www.drhuang.com/chinese/science/mathematics/handbook/GC3/GC3.htm
参考链接：http://www.drhuang.com/chinese/science/mathematics/handbook/GC4/GC4.htm
第二基本二次型曲面曲线的曲率
[第二基本二次型与第二基本量]
百度解答：
已知曲面z=a0+a1x+a2y+a3xy+a4x^2+a5y^2的系数a0,a1,a2,a3,a4,a5，如何求曲面的第一基本量,第二基本量？？
先求 u = dz/dx, v = dz/dy, 然后再求baip = du/dx, q = dv/dy, r = zhi/dy , 继而求得曲dao面的zhuan法向量shu
n = u×v / |u×v|; 由此回可以算出曲面的第一基本量答 E = u^2; F = uv; G = v^2; 第二基本量:L = p*n, M = r*n, N = q*n。
以下是这个链接博主的推导过程和代码，以及结果，超级感谢指导。大牛博主链接：https://blog.csdn.net/qq_36686437/article/details/109350523
#include
#include
#include
#include
#include //kdtree近邻搜索
using namespace std;
using namespace Eigen;
int main()
{
//-----------------读取点云数据--------------------
pcl::PointCloud::Ptr cloud(new pcl::PointCloud);
if (pcl::io::loadPCDFile("desk2.pcd", *cloud) == -1)
{
PCL_ERROR("Cloudn't read file!");
return -1;
}
//---------------矩阵运算相关参数-------------------
MatrixXd Mean_curvature;
Mean_curvature.resize(cloud->size(), 1); //初始化矩阵 cloud->size * 1；
MatrixXd Gauss_curvature;
Gauss_curvature.resize(cloud->size(), 1);
MatrixQ; //求解方程组系数矩阵
MatrixQ_Inverse; //系数矩阵的逆矩阵
MatrixB; //方程组右值矩阵
Q.setZero(); //初始化矩阵元素全为0
Q_Inverse.setZero();
B.setZero();
double a = 0, b = 0, c = 0, d = 0, e = 0, f = 0;//二次曲面方程系数
double u = 0, v = 0; //二次曲面参数方程参数
double E = 0, G = 0, F = 0, L = 0, M = 0, N = 0;//曲面第一、第二基本量
double Meancurvature = 0, Gausscurvature = 0; //平均曲率、高斯曲率
//------------K近邻搜索查找最近点----------------
pcl::KdTreeFLANN kdtree;
kdtree.setInputCloud(cloud);
for (size_t i_p = 0; i_p < cloud->points.size(); ++i_p) {
pcl::PointXYZ searchPoint = cloud->points[i_p]; //设置查找点
int K = 10; //设置需要查找的近邻点个数
vector pNK(K); // 保存每个近邻点的索引
vector pointNKNSquaredDistance(K); // 保存每个近邻点与查找点之间的欧式距离平方
if (kdtree.nearestKSearch(searchPoint, K, pNK, pointNKNSquaredDistance) > 0)
{
for (size_t i = 0; i < pNK.size(); ++i) {
cloud->points[pNK[i]];
//---------------构建最小二乘平差计算矩阵-------------------
Q(0, 0) += pow(cloud->points[pNK[i]].x, 4);
Q(1, 0) = Q(0, 1) += pow(cloud->points[pNK[i]].x, 3) * cloud->points[pNK[i]].y;
Q(2, 0) = Q(0, 2) += pow(cloud->points[pNK[i]].x * cloud->points[pNK[i]].y, 2);
Q(3, 0) = Q(0, 3) += pow(cloud->points[pNK[i]].x, 3);
Q(4, 0) = Q(0, 4) += pow(cloud->points[pNK[i]].x, 2) * cloud->points[pNK[i]].y;
Q(5, 0) = Q(0, 5) += pow(cloud->points[pNK[i]].x, 2);
Q(1, 1) += pow(cloud->points[pNK[i]].x * cloud->points[pNK[i]].y, 2);
Q(2, 1) = Q(1, 2) += pow(cloud->points[pNK[i]].y, 3) * cloud->points[pNK[i]].x;
Q(3, 1) = Q(1, 3) += pow(cloud->points[pNK[i]].x, 2) * cloud->points[pNK[i]].y;
Q(4, 1) = Q(1, 4) += pow(cloud->points[pNK[i]].y, 2) * cloud->points[pNK[i]].x;
Q(5, 1) = Q(1, 5) += cloud->points[pNK[i]].x * cloud->points[pNK[i]].y;
Q(2, 2) += pow(cloud->points[pNK[i]].y, 4);
Q(3, 2) = Q(2, 3) += pow(cloud->points[pNK[i]].y, 2) * cloud->points[pNK[i]].x;
Q(4, 2) = Q(2, 4) += pow(cloud->points[pNK[i]].y, 3);
Q(5, 2) = Q(2, 5) += pow(cloud->points[pNK[i]].y, 2);
Q(3, 3) += pow(cloud->points[pNK[i]].x, 2);
Q(4, 3) = Q(3, 4) += cloud->points[pNK[i]].x * cloud->points[pNK[i]].y;
Q(5, 3) = Q(3, 5) += cloud->points[pNK[i]].x;
Q(4, 4) += pow(cloud->points[pNK[i]].y, 2);
Q(5, 4) = Q(4, 5) += cloud->points[pNK[i]].y;
Q(5, 5) += 1;
B(0, 0) += pow(cloud->points[pNK[i]].x, 2) * cloud->points[pNK[i]].z;
B(1, 0) += cloud->points[pNK[i]].x * cloud->points[pNK[i]].y * cloud->points[pNK[i]].z;
B(2, 0) += pow(cloud->points[pNK[i]].y, 2) * cloud->points[pNK[i]].z;
B(3, 0) += cloud->points[pNK[i]].x * cloud->points[pNK[i]].z;
B(4, 0) += cloud->points[pNK[i]].y * cloud->points[pNK[i]].z;
B(5, 0) += cloud->points[pNK[i]].z;
//---------------求解矩阵------------------
Q_Inverse =Q.inverse();
for (int j = 0; j < 6; ++j)
{
a += Q_Inverse(0, j) * B(j, 0);
b += Q_Inverse(1, j) * B(j, 0);
c += Q_Inverse(2, j) * B(j, 0);
d += Q_Inverse(3, j) * B(j, 0);
e += Q_Inverse(4, j) * B(j, 0);
f += Q_Inverse(5, j) * B(j, 0);
}
// 根据所求曲面方程的系数计算曲面第一第二基本量
u = 2 * a * cloud->points[pNK[i]].x + b * cloud->points[pNK[i]].y + d;
v = 2 * c * cloud->points[pNK[i]].y + b * cloud->points[pNK[i]].x + e;
E = 1 + u * u;
F = u * v;
G = 1 + v * v;
double u_v = sqrt(1 + u * u + v * v);
L = (2 * a) / u_v;
M = b / u_v;
N = (2 * c) / u_v;
// 高斯曲率
Gausscurvature = (L * N - M * M) / (E * G - F * F);
Gauss_curvature(i_p, 0) = Gausscurvature;
// 平均曲率
Meancurvature = (E * N - 2 * F * M + G * L) / (2 * E * G - 2 * F * F);
Mean_curvature(i_p, 0) = Meancurvature;
}
}
}
cout << "高斯曲率为：" << Gauss_curvature(1, 0) << endl;
return 0;
} 