《统计学习方法》读书笔记——感知机(原理+代码实现)
传送门
《统计学习方法》读书笔记——机器学习常用评价指标
《统计学习方法》读书笔记——感知机(原理+代码实现)
《统计学习方法》读书笔记——K近邻法(原理+代码实现)
《统计学习方法》读书笔记——朴素贝叶斯法(公式推导+代码实现)
感知机
-
- 传送门
- 一、感知机的定义
- 二、感知机学习策略
- 三、感知机学习算法
- 四、代码实现
- 参考
一、感知机的定义
假设输入空间 X ⊆ R n \mathcal{X}\subseteq{\mathcal{R^n}} X⊆Rn,输出空间 Y = { + 1 , − 1 } \mathcal{Y} = \{+1, -1\} Y={+1,−1};
输入 x ∈ X x\in\mathcal{X} x∈X表示样本的特征向量,输出 y ∈ Y y\in\mathcal{Y} y∈Y表示样本的类别。则由输入空间到输出空间的映射(函数)
f ( x ) = s i g n ( w ⋅ x + b ) f(x)=sign(w \cdot x + b) f(x)=sign(w⋅x+b)
称为感知机,其中 w ∈ R n w\in\mathcal{R^n} w∈Rn称为权值, b ∈ R b\in\mathcal{R} b∈R称为偏置, s i g n sign sign为符号函数。
二、感知机学习策略
感知机学习的目标即找出能够将训练数据集中的正、负样本分离开的超平面。 如图:
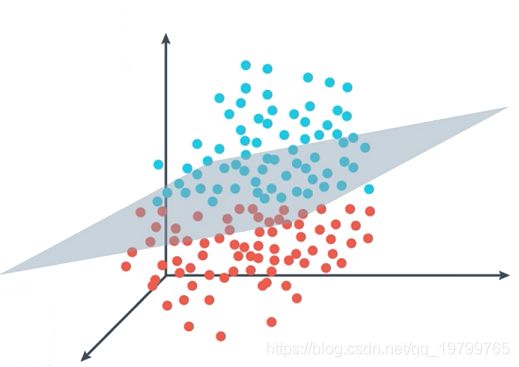
定义损失函数为所有错误分类的样本点到超平面的距离之和。推导如下:
输入空间任意一点 x 0 x_0 x0到超平面的距离为:
1 ∥ w ∥ ∣ w ⋅ x 0 + b ∣ \frac{1}{\|w\|} |w\cdot x_0+b| ∥w∥1∣w⋅x0+b∣
其中 ∥ w ∥ \|w\| ∥w∥是 w w w的 L 2 L_2 L2范数,即各元素的平方和再开平方。
\\
对分类错误的样本点来说 − y i ( w ⋅ x i + b ) > 0 -y_i(w\cdot x_i + b)>0 −yi(w⋅xi+b)>0,因此
∣ w ⋅ x 0 + b ∣ = − y i ( w ⋅ x i + b ) |w\cdot x_0 + b| = -y_i(w\cdot x_i + b) ∣w⋅x0+b∣=−yi(w⋅xi+b)
则错误分类的样本点到超平面的总距离为: − 1 ∥ w ∥ ∑ x i ∈ M y i ( w ⋅ x i + b ) -\frac{1}{\|w\|}\sum\limits_{x_i\in M}{y_i(w\cdot x_i+b)} −∥w∥1xi∈M∑yi(w⋅xi+b)
若不考虑 ∥ w ∥ \|w\| ∥w∥,则损失函数定义如下:
L ( w , b ) = − ∑ x i ∈ M y i ( w ⋅ x i + b ) L(w,b) = -\sum\limits_{x_i\in M}{y_i(w\cdot x_i+b)} L(w,b)=−xi∈M∑yi(w⋅xi+b)
三、感知机学习算法
输入:训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋅ ⋅ ⋅ , ( x n , y n ) } T=\{ (x_1,y_1),(x_2,y_2),···,(x_n,y_n)\} T={(x1,y1),(x2,y2),⋅⋅⋅,(xn,yn)},其中 x i ∈ X = R n x_i\in\mathcal{X}=\mathcal{R^n} xi∈X=Rn, y i ∈ Y = { − 1 , + 1 } , i = 1 , 2 , ⋅ ⋅ ⋅ , n y_i\in\mathcal{Y}= \{-1,+1\},i=1,2,···,n yi∈Y={−1,+1},i=1,2,⋅⋅⋅,n;学习率 η ( 0 < η ≤ 1 ) \eta(0<\eta\leq1) η(0<η≤1);
输出: w , b w,b w,b;感知机模型 f ( x ) = s i g n ( w ⋅ x + b ) f(x)=sign(w\cdot x+b) f(x)=sign(w⋅x+b)。
(1)选取初值 w 0 , b 0 w_0,b_0 w0,b0;
(2)在训练集中选取数据 ( x i , y i ) (x_i,y_i) (xi,yi);
(3)如果 y i ( w ⋅ x i + b ) ≤ 0 y_i(w\cdot x_i+b)\leq0 yi(w⋅xi+b)≤0;
w ← w + η y i x i b ← b + η y i w\larr w+\eta y_i x_i \\ b\larr b+\eta y_i w←w+ηyixib←b+ηyi
(4)转至(2),直至训练集中没有误分类点。
四、代码实现
#coding=utf-8
import numpy as np
import time
def loadData(fileName):
print('start to read data')
dataArr = []
labelArr = []
fr = open(fileName, 'r')
# 将文件按行读取
for line in fr.readlines():
# 对每一行数据按切割符','进行切割,返回字段列表
curLine = line.strip().split(',')
# Mnsit有0-9是个标记,由于是二分类任务,所以将>=5的作为1,<5为-1
if int(curLine[0]) >= 5:
labelArr.append(1)
else:
labelArr.append(-1)
#存放标记
#[int(num) for num in curLine[1:]] -> 遍历每一行中除了以第一哥元素(标记)外将所有元素转换成int类型
#[int(num)/255 for num in curLine[1:]] -> 将所有数据除255归一化(非必须步骤,可以不归一化)
dataArr.append([int(num)/255 for num in curLine[1:]])
#返回data和label
return dataArr, labelArr
def perceptron(dataArr, labelArr, iter=50):
print('start to train...')
dataMat = np.array(dataArr)
labelMat = np.array(labelArr)
#获取数据矩阵的大小,为m*n
m, n = np.shape(dataMat)
# w为权重,随机初始化, shape为 784*1
# b为偏置,初始化为0
# eta为学习率,控制梯度下降速度
w = np.random.rand(1, n)
b = 0
eta = 0.001
#进行iter次迭代计算
for k in range(iter):
# 随机梯度下降
for i in range(m):
# 当前样本的特征向量,及样本类别
xi = dataMat[i].reshape(-1, 1)
yi = labelMat[i]
#判断是否是误分类样本
if -1 * yi * (w @ xi + b) > 0:
#对于误分类样本,进行梯度下降,更新w和b
w = w + eta * yi * xi.T
b = b + eta * yi
#打印训练进度
print('Round %d:%d training' % (k, iter))
#返回训练完的w、b
return w, b
def model_test(dataArr, labelArr, w, b):
print('start to test...')
dataMat = np.array(dataArr)
labelMat = np.array(labelArr)
#获取测试数据集矩阵的大小
m, n = np.shape(dataMat)
#错误样本数计数
errorCnt = 0
for i in range(m):
# 当前样本的特征向量,及样本类别
xi = dataMat[i]
yi = labelMat[i]
# 运算结果
result = -1 * yi * (w * xi.T + b)
#如果-yi(w*xi+b)>=0,说明该样本被误分类,错误样本数加一
if result >= 0:
errorCnt += 1
# 计算并返回正确率
accruRate = 1 - (errorCnt / m)
return accruRate
if __name__ == '__main__':
start = time.time()
trainData, trainLabel = loadData('./mnist/mnist_train.csv')
testData, testLabel = loadData('./mnist/mnist_test.csv')
#训练获得权重
w, b = perceptron(trainData, trainLabel, iter = 30)
#进行测试,获得正确率
accruRate = model_test(testData, testLabel, w, b)
end = time.time()
print('accuracy rate is:', accruRate)
print('time span:', end - start)
参考
原理:《统计学习方法》
代码: https://github.com/Dod-o/Statistical-Learning-Method_Code
