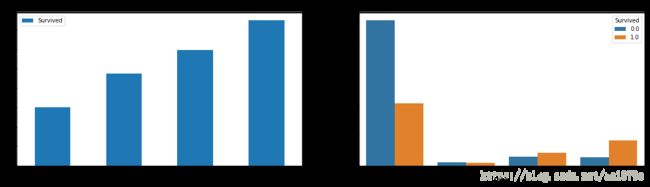数据竞赛入门题 Tatanic | top_5%解法及数据分析常用技巧详解
Titanic:
身为女性且来自头等舱的ROSE存活率高达95%,身为男性且来自二等舱的Jack存活率不足10%。悲剧似乎在他们上船的那一刻就已经注定了。
日期:2018/10/07
1.任务简介
泰坦尼克号的沉没是历史上最著名的沉船之一。1912年4月15日,在她的处女航中,泰坦尼克号在与冰山相撞后沉没,在2224名乘客和机组人员中造成1502人死亡。这场耸人听闻的悲剧震惊了国际社会,并促使各国制定了更好的船舶安全规定。
造成海难失事的原因之一是乘客和机组人员没有足够的救生艇。尽管幸存有一些运气因素,但有些人比其他人更容易生存,比如女人,孩子和上流社会。
在这个挑战中,我们要求您完成对哪些人可能存活进行分析。特别地,我们要求您运用机器学习工具来预测哪些乘客能够幸免于悲剧。
2.数据分析
import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# sns.set_style('white')
from sklearn.neural_network import MLPClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split, learning_curve, ShuffleSplit, GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier, GradientBoostingClassifier, ExtraTreesClassifier, VotingClassifier
from sklearn.metrics import f1_score, accuracy_score, classification_report
定义函数 load_data
def load_data():
home_path = "data"
train_path = os.path.join(home_path, "train.csv")
test_path = os.path.join(home_path, "test.csv")
submit_path = os.path.join(home_path, "gender_submission.csv")
train_data = pd.read_csv(train_path)
test_data = pd.read_csv(test_path)
submit_data = pd.read_csv(submit_path)
# 去掉第一列
train_data.drop("PassengerId", axis=1, inplace=True)
test_data.drop("PassengerId", axis=1, inplace=True)
# train_data.drop("Name", axis=1, inplace=True)
# test_data.drop("Name", axis=1, inplace=True)
return train_data, test_data, submit_data
概览
可以看到训练集有891个样本,测试集有418个样本,除去是否幸存这个target变量,共有10个特征变量
trainData, testData, submitData = load_data()
print('train Data:{} testData:{}'.format(trainData.shape, testData.shape))
train Data:(891, 11) testData:(418, 10)
特征名含义
这十个特征的含义如下:
Pclass:头等舱,二等舱...
Name:姓名
Sex:性别
Age:年龄
SibSp:该乘客在船上兄弟姐妹或妻子的数量
Parch:该乘客在船上父母或孩子的数量
Ticket:船票
Fare:费用
Cabin:船舱
Embarked: 出发港口
另外还有一个target variable
survival:幸存(1),遇难(0)
数据大概长什么样子?
trainData.head()
| Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
print(trainData.describe())
Survived Pclass Age SibSp Parch Fare
count 891.000000 891.000000 714.000000 891.000000 891.000000 891.000000
mean 0.383838 2.308642 29.699118 0.523008 0.381594 32.204208
std 0.486592 0.836071 14.526497 1.102743 0.806057 49.693429
min 0.000000 1.000000 0.420000 0.000000 0.000000 0.000000
25% 0.000000 2.000000 20.125000 0.000000 0.000000 7.910400
50% 0.000000 3.000000 28.000000 0.000000 0.000000 14.454200
75% 1.000000 3.000000 38.000000 1.000000 0.000000 31.000000
max 1.000000 3.000000 80.000000 8.000000 6.000000 512.329200
哪些数据有缺失?
trainData.isnull().sum()
Survived 0
Pclass 0
Name 0
Sex 0
Age 177
SibSp 0
Parch 0
Ticket 0
Fare 0
Cabin 687
Embarked 2
dtype: int64
testData.isnull().sum()
Pclass 0
Name 0
Sex 0
Age 86
SibSp 0
Parch 0
Ticket 0
Fare 1
Cabin 327
Embarked 0
dtype: int64
有多少人幸存下来了?
plt.subplots(figsize=[6,6])
trainData['Survived'].value_counts().plot(kind='pie',autopct='%.1f%%')
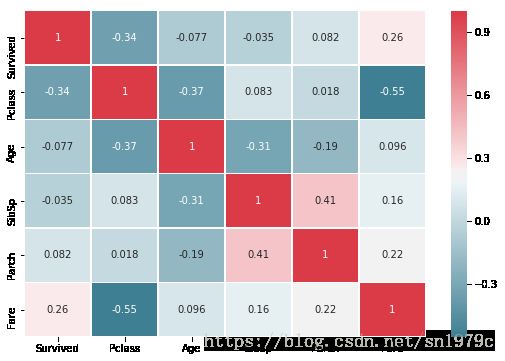
相关性
# print(trainData.corr())
cmap = sns.diverging_palette(220, 10, as_cmap=True)
ax = plt.subplots(figsize=(9, 6))
sns.heatmap(trainData.corr(),annot=True,cmap = cmap , linewidths=.5, )
从列表第一列可以看出未处理的各个数据和幸存与否的关系
变量研究
变量分类
特征变量常可以分为:Categorical Features, Ordinal Features, Continous Feature。
Categorical Features往往代表某种事件的类型,比如Sex, Embarked。
Ordinal Features 也代表了事件的某些类型,但这些类型往往可以排序,身高往往可以分为高中矮。Pclass。
Continous Feature 可能是某个区间上的任意数值,比如Age。
Sex
f, ax = plt.subplots(1, 2, figsize=(10, 5))
trainData[['Survived', 'Sex']].groupby(['Sex']).mean().plot(kind='bar', ax=ax[0])
sns.countplot('Sex',hue='Survived',data=trainData,ax=ax[1])
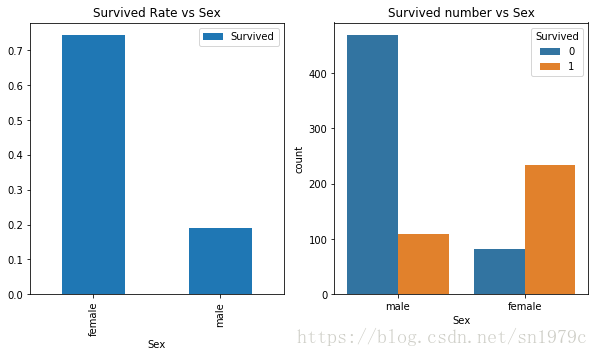
ax[0].set_title('Survived Rate vs Sex')
ax[1].set_title('Survived number vs Sex')
# sns.countplot(data=trainData, hue='Sex','Survived', ax=ax[1])
Text(0.5,1,'Survived number vs Sex')
可以明显地看到,女性的生存概率高于男性
Pclass
f, ax =plt.subplots(1, 2, figsize=(10, 5))
trainData[['Pclass', 'Survived']].groupby(['Pclass']).mean().plot(kind='bar', ax=ax[0])
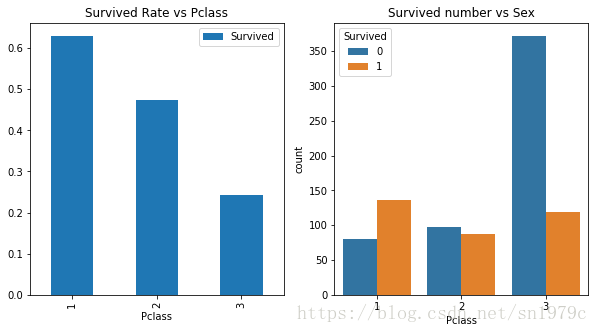
ax[0].set_title('Survived Rate vs Pclass')
sns.countplot('Pclass', hue='Survived', data=trainData, ax=ax[1])
ax[1].set_title('Survived number vs Sex')
Text(0.5,1,'Survived number vs Sex')
可以看到,处于越高阶级的人存活率越高。
Embarked
f, ax =plt.subplots(1, 2, figsize=(10, 5))
trainData[['Embarked', 'Survived']].groupby(['Embarked']).mean().plot(kind='bar', ax=ax[0])
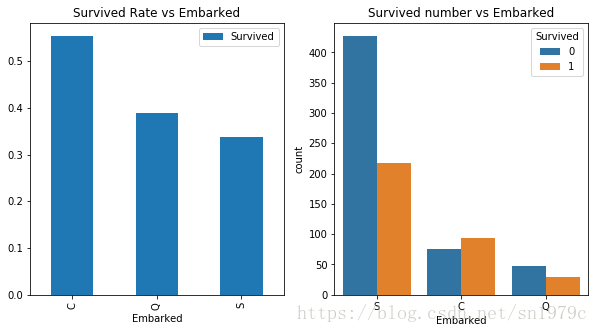
ax[0].set_title('Survived Rate vs Embarked')
sns.countplot('Embarked', hue='Survived', data=trainData, ax=ax[1])
ax[1].set_title('Survived number vs Embarked')
Text(0.5,1,'Survived number vs Embarked')
有趣的是,名义变量Embarked也与存活率有关,从不同港口出发的存活率也不一样。
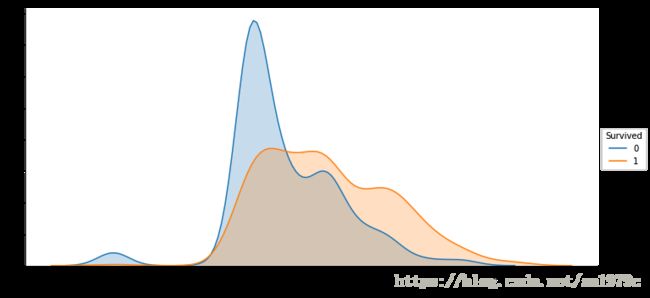
sns.FacetGrid(trainData, hue='Survived', aspect=2, size=5).map(sns.kdeplot, 'Fare', shade=True).add_legend()
可以看到,Fare的分布偏斜度太大,我们对其取+1取对数
x = pd.DataFrame()
x['Fare'] = trainData['Fare'].map(lambda x: np.log(x+1))
x['Survived'] = trainData['Survived']
sns.FacetGrid(x, hue='Survived', aspect=2, size=5).map(sns.kdeplot, 'Fare', shade=True).add_legend()
可以看到,有钱人的生存概率明显较高。
组合分析
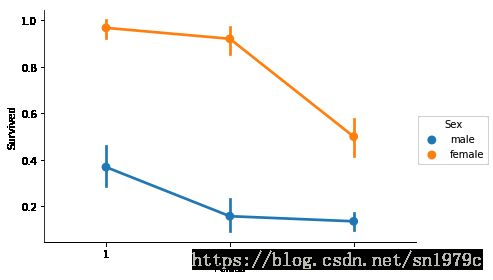
f = sns.factorplot('Pclass', 'Survived', hue='Sex', data=trainData, size=4, aspect=1.5)
可以看出女性贵族的存活率非常高,接近100%
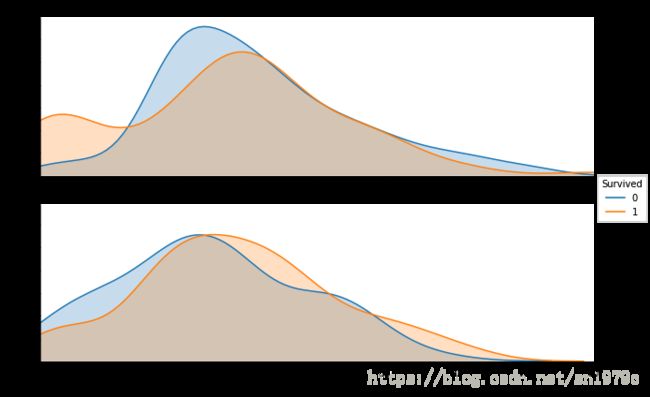
sns.FacetGrid(trainData, row='Sex' , hue='Survived', aspect=3, size=3).map(
sns.kdeplot , 'Age' , shade=True ).set(xlim=(trainData['Age'].min(),trainData['Age'].max())).add_legend()
可以看到中青年男性和青少年女性存活率较低,幼年老年男性,中年女性存活率较低。
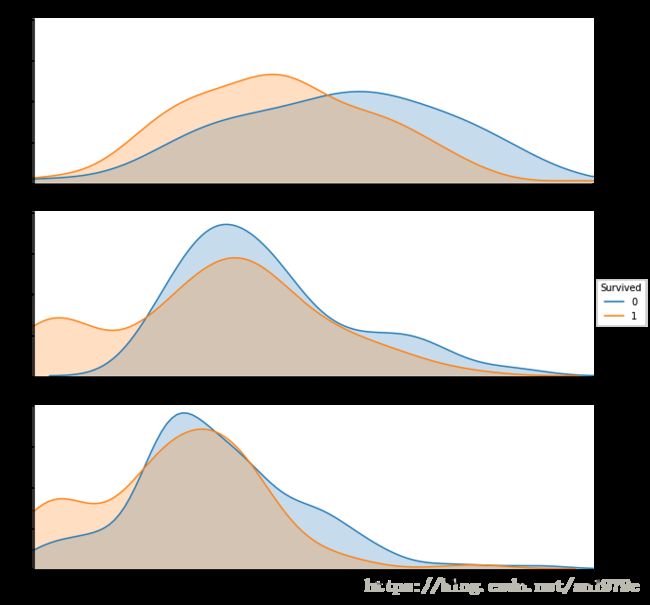
sns.FacetGrid(trainData, row='Pclass', hue='Survived', aspect=3, size=3).map(
sns.kdeplot, 'Age', shade=True).set(xlim=(trainData['Age'].min(),trainData['Age'].max())).add_legend()
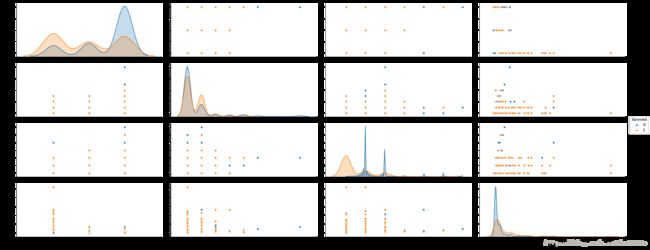
利用seaborn的函数pairplot可以分析:
- 各个numeric variable之间的关系(非对角的图)
- 各个数值特征变量的分布对target variable 'Survived'的影响。(对角的图)
# 图'Parch'-'Parch'有bug,但在pycharm中运行正常
sns.pairplot(trainData,vars = ['Pclass', 'SibSp', 'Parch', 'Fare'], aspect = 2.5, size = 2.5,
hue = 'Survived', diag_kind = 'kde', diag_kws=dict(shade=True))
数据预处理
将类型变量转换为数值变量:Sex, Embarked
将类型变量转换为数值变量一般这样做:对于只有两类的类型变量,将其转换为一列(01)数值变量,对于n(n>2)类的类型变量,将其转换为n列01数值变量。
Embarked, Sex为类型变量,Sex为只有两类的类型变量,Embarked为有三类的类型变量。
full = trainData.append(testData, ignore_index=True, sort=False)
Sex = pd.Series(np.where(full['Sex']=='male', 1, 0), name='Sex')
Embarked= pd.get_dummies(full['Embarked'],prefix='Embarked')
print(Embarked.head())
Embarked_C Embarked_Q Embarked_S
0 0 0 1
1 1 0 0
2 0 0 1
3 0 0 1
4 0 0 1
提取出姓名中的称呼:Name–title
full['title'] = 0
full['title'] = full['Name'].map(lambda name:name.split(',')[1].split('.')[0].strip(',. '))
# 显示所有的Title种类
titleUnique = full['title'].drop_duplicates()
print(np.array(titleUnique).T)
['Mr' 'Mrs' 'Miss' 'Master' 'Don' 'Rev' 'Dr' 'Mme' 'Ms' 'Major' 'Lady'
'Sir' 'Mlle' 'Col' 'Capt' 'the Countess' 'Jonkheer' 'Dona']
full['title'].replace(
['Mlle','Mme','Ms','Dr','Major','Lady','the Countess','Jonkheer','Col','Rev','Capt','Sir','Dona', 'Don'],
['Miss','Miss','Miss','Mr','Mr','Mrs','Mrs','Other','Other','Other','Mr','Mr','Mrs','Mr'],inplace=True)
title = pd.get_dummies(full['title'],prefix='Titile')
title.head()
| Titile_Master | Titile_Miss | Titile_Mr | Titile_Mrs | Titile_Other | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
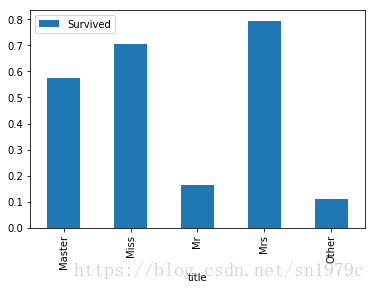
可以看到title这个变量还是相当有区分度的。
full[['title', 'Survived']].groupby('title').mean().plot(kind='bar')
补全残缺样本:Fare, Age
对于数值变量,最简单的方法是通过将缺失数据填补为平均数来构造新的样本。填补NaN的函数为[Dataframe].fillna()
我们通过称呼来填补年龄,用平均值来填补Fare
full.loc[full['Fare'].isnull(),'Fare'] = full['Fare'].mean()
fare = full['Fare'].map(lambda x:np.log(x+1))
full.groupby('title')['Age'].mean()
title
Master 5.482642
Miss 21.834533
Mr 32.545531
Mrs 37.046243
Other 44.923077
Name: Age, dtype: float64
full.loc[full['title']=='Master', 'Age'] = 6
full.loc[full['title']=='Miss', 'Age'] = 22
full.loc[full['title']=='Mr', 'Age'] = 33
full.loc[full['title']=='Mrs', 'Age'] = 37
full.loc[full['title']=='Other', 'Age'] = 45
age = full['Age']
age.isnull().any()
False
构建新样本:cabin(4)
cabin = pd.DataFrame()
full['Cabin'] = full.Cabin.fillna('U')
# 这样会出错:cabin['Cabin'] = full['Carbin'].fillna('U')
cabin['Cabin'] = full.Cabin.map(lambda cabin:cabin[0])
full['Cabin'] = cabin['Cabin']
# cabin = pd.get_dummies(cabin['Cabin'], prefix='Cabin')
# print(cabin.head())
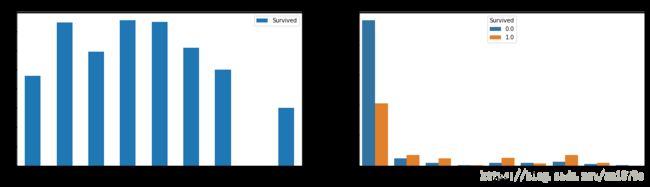
f, ax = plt.subplots(1, 2, figsize=(20,5))
full[['Cabin', 'Survived']].groupby(['Cabin']).mean().plot(kind='bar',ax=ax[0])
sns.countplot('Cabin', hue='Survived', data=full, ax=ax[1])
ax[0].set_title('Survived Rate vs Cabin')
ax[1].set_title('Survived countvs Cabin')
plt.show()
print(full['Cabin'].value_counts())
U 1014
C 94
B 65
D 46
E 41
A 22
F 21
G 5
T 1
Name: Cabin, dtype: int64
将较少的样本并入与其存活率相近的样本,将存活率相近的样本合并:
将TU合并,将AG合并,将BDE合并,将CF合并。
full.loc[full.Cabin=='T', 'Cabin'] = 1
full.loc[full.Cabin=='U', 'Cabin'] = 1
full.loc[full.Cabin=='A', 'Cabin'] = 2
full.loc[full.Cabin=='G', 'Cabin'] = 2
full.loc[full.Cabin=='C', 'Cabin'] = 3
full.loc[full.Cabin=='F', 'Cabin'] = 3
full.loc[full.Cabin=='B', 'Cabin'] = 4
full.loc[full.Cabin=='D', 'Cabin'] = 4
full.loc[full.Cabin=='E', 'Cabin'] = 4
cabin = pd.get_dummies(full['Cabin'], prefix='Cabin')
cabin.head()
| Cabin_1 | Cabin_2 | Cabin_3 | Cabin_4 | |
|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 1 | 0 | 0 | 0 |
| 3 | 0 | 0 | 1 | 0 |
| 4 | 1 | 0 | 0 | 0 |
f, ax = plt.subplots(1, 2, figsize=(20,5))
full[['Cabin', 'Survived']].groupby(['Cabin']).mean().plot(kind='bar',ax=ax[0])
sns.countplot('Cabin', hue='Survived', data=full, ax=ax[1])
ax[0].set_title('Survived Rate vs Cabin')
ax[1].set_title('Survived countvs Cabin')
plt.show()
print(full['Cabin'].value_counts())
1 1015
4 152
3 115
2 27
Name: Cabin, dtype: int64
这样,Cabin就被转化为了4个类型变量
构建新样本,Ticket–11个类型变量ticket
ticket = pd.DataFrame()
delete_chars = str.maketrans('./',' ')
ticket['Ticket'] = full['Ticket'].map(lambda ticket: np.where(ticket.isnumeric(), 'NumTicket',
''.join(ticket.translate(delete_chars).split()[:-1])))
ticket.loc[ticket['Ticket']=='', :] = 'LINE'
full['Ticket'] = ticket['Ticket']
# ticket = pd.get_dummies(ticket)
# print(ticket.describe())
将训练集中样本量小于5的票型归入RARE,纯数字的票型归为NumTicket,这样就从Ticket中提取出了11个类型变量。
x = full.loc[~full['Survived'].isnull(),'Ticket'].value_counts()>5
x = x[x].index
full['Ticket'] = full['Ticket'].map(lambda t: np.where(t in x, t, 'RARE'))
f, ax = plt.subplots(1, 2, figsize=(20,5))
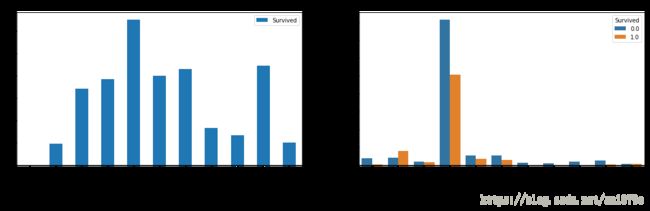
full[['Ticket', 'Survived']].groupby(['Ticket']).mean().plot(kind='bar',ax=ax[0])
sns.countplot('Ticket', hue='Survived', data=full, ax=ax[1])
ax[0].set_title('Survived Rate vs Ticket')
ax[1].set_title('Survived countvs Ticket')
plt.show()
ticket = pd.get_dummies(full['Ticket'],prefix='tic')
ticket.head()
| tic_A4 | tic_A5 | tic_CA | tic_NumTicket | tic_PC | tic_RARE | tic_SCPARIS | tic_SOC | tic_SOTONOQ | tic_STONO2 | tic_WC | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
SibSp, Parch—家庭规模(3)
可以将SibSp和Parch构建为新的类型变量–家庭规模
family = pd.DataFrame()
family['family_size'] = full['SibSp'] + full['Parch'] + 1
family['family_single_size'] = family['family_size'].map(lambda size: np.where(size == 1, 1, 0))
family['family_small_size'] = family['family_size'].map(lambda size: np.where(size >= 2 and size<=4, 1, 0))
family['family_big_size'] = family['family_size'].map(lambda size: np.where(size >= 5, 1, 0))
family = family.loc[:, 'family_single_size':'family_big_size']
print(family.head())
family_single_size family_small_size family_big_size
0 0 1 0
1 0 1 0
2 1 0 0
3 0 1 0
4 1 0 0
序列变量Pclass不变
Pclass = full['Pclass']
选择特征变量
已构造好的特征变量如下,共30个变量,我们先全部用上
- family(3)
- ticket(11)
- cabin(4)
- Pclass(3)
- Embarked(3)
- Sex(1)
- title(5)
- age
- fare
full_X = pd.concat([family, ticket, cabin, Pclass, Embarked, Sex, title, age, fare], axis=1)
# full_X = pd.concat([family, Pclass, Embarked, Sex, age, fare], axis=1)
print(full_X.head())
family_single_size family_small_size family_big_size tic_A4 tic_A5 \
0 0 1 0 0 1
1 0 1 0 0 0
2 1 0 0 0 0
3 0 1 0 0 0
4 1 0 0 0 0
tic_CA tic_NumTicket tic_PC tic_RARE tic_SCPARIS ... Embarked_Q \
0 0 0 0 0 0 ... 0
1 0 0 1 0 0 ... 0
2 0 0 0 0 0 ... 0
3 0 1 0 0 0 ... 0
4 0 1 0 0 0 ... 0
Embarked_S Sex Titile_Master Titile_Miss Titile_Mr Titile_Mrs \
0 1 1 0 0 1 0
1 0 0 0 0 0 1
2 1 0 0 1 0 0
3 1 0 0 0 0 1
4 1 1 0 0 1 0
Titile_Other Age Fare
0 0 33.0 2.110213
1 0 37.0 4.280593
2 0 22.0 2.188856
3 0 37.0 3.990834
4 0 33.0 2.202765
[5 rows x 30 columns]
建模训练
train_valid_X = full_X[0:891]
train_valid_y = trainData['Survived']
train_X, valid_X, train_y, valid_y = train_test_split(train_valid_X, train_valid_y, test_size=0.2, random_state=20)
model = DecisionTreeClassifier( random_state = 0 )
model.fit( train_X , train_y )
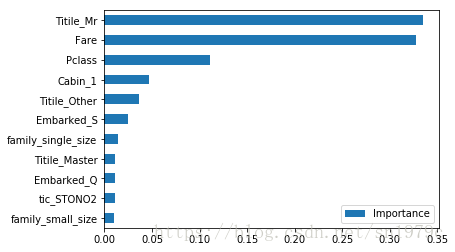
importance = pd.DataFrame(model.feature_importances_,
columns=['Importance'],
index=train_valid_X.columns)
importance = importance.sort_values(['Importance'], ascending=False)[0:11]
importance[::-1].plot(kind='barh')
print(model.score(valid_X , valid_y))
0.8156424581005587
算法选择
初步地看看各个算法的效果,通过多次不同的样本分类来消除分类对打分带来的噪声。可以看到GradientBoosting的准确率最高,最终决定选择GradientBoosting算法
按理说选参数应该先把各个模型参数的量级调一遍,这样可以减少默认参数造成的算法歧视。
score = np.zeros(9)
classifier = ['DecisionTreeClassifier', 'RandomForestClassifier', 'SVC',
'GradientBoostingClassifier', 'KNeighborsClassifier', 'GaussianNB',
'LogisticRegression', 'ExtraTreesClassifier', 'MLPClassifier']
for i in range(30):
random_state=i
train_X, valid_X, train_y, valid_y = train_test_split(train_valid_X, train_valid_y, test_size=0.2)
model = DecisionTreeClassifier(random_state=random_state).fit(train_X, train_y)
score[0] += accuracy_score(valid_y, model.predict(valid_X))
model = RandomForestClassifier(random_state=random_state, n_estimators=100).fit(train_X, train_y)
score[1] += accuracy_score(valid_y, model.predict(valid_X))
model = SVC().fit(train_X, train_y)
score[2] += accuracy_score(valid_y, model.predict(valid_X))
model = GradientBoostingClassifier(random_state=random_state).fit(train_X, train_y)
score[3] += accuracy_score(valid_y, model.predict(valid_X))
model = KNeighborsClassifier(n_neighbors = 3).fit(train_X, train_y)
score[4] += accuracy_score(valid_y, model.predict(valid_X))
model = GaussianNB().fit(train_X, train_y)
score[5] += accuracy_score(valid_y, model.predict(valid_X))
model = LogisticRegression().fit(train_X, train_y)
score[6] += accuracy_score(valid_y, model.predict(valid_X))
model = ExtraTreesClassifier(random_state=random_state).fit(train_X, train_y)
score[7] += accuracy_score(valid_y, model.predict(valid_X))
model = MLPClassifier(random_state=random_state).fit(train_X, train_y)
score[8] += accuracy_score(valid_y, model.predict(valid_X))
score = score/30
classifierScore = {classifier[i]:score[i] for i in range(len(score))}
classifierScore = pd.Series(classifierScore)
classifierScore.sort_values().plot(kind='barh', xlim=[0.5, 0.85])
plt.ylabel('accuracy')
plt.xlabel('classifier')
Text(0.5,0,'classifier')
学习曲线
调参前可以先画出learning curve来看看默认参数处于高偏差还是高方差。
若参数处于高方差的状态,可以首先由以下通用方法来改善预测结果:
- 获取更多的样本
- 减少特征变量的数量
- 减小模型复杂度(如增大正则化参数lambda)
若参数处于高偏差的状态,可以由以下的通用方法来改善预测结果:
- 构造更多的特征变量
- 增加模型复杂度
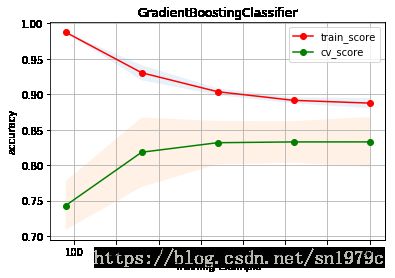
实际上高偏差对应的状态是过拟合,而高方差对应的状态是欠拟合。从画出的leaning curve可以看出,虽然拟合的不错,但其实还是有点过拟合
def plot_learning_curve(estimater, title, X, y, cv):
sizes, train_scores, cv_scores = learning_curve(estimater, train_valid_X, train_valid_y, cv=cv, scoring='accuracy')
plt.title(title)
plt.xlabel('Training Example')
plt.ylabel('accuracy')
# plt.ylim([0.5, 1.01])
train_error_mean = np.mean(train_scores, axis=1)
train_error_std = np.std(train_scores, axis=1)
cv_error_mean = np.mean(cv_scores, axis=1)
cv_error_std = np.std(cv_scores, axis=1)
plt.fill_between(sizes, y1=train_error_mean-train_error_std, y2=train_error_mean+train_error_std, alpha=0.1)
plt.fill_between(sizes, y1=cv_error_mean-cv_error_std, y2=cv_error_mean+cv_error_std, alpha=0.1)
plt.grid()
plt.plot(sizes, train_error_mean, 'o-', color='r', label='train_score')
plt.plot(sizes, cv_error_mean, 'o-', color='g', label='cv_score')
plt.legend(loc='best')
return plt
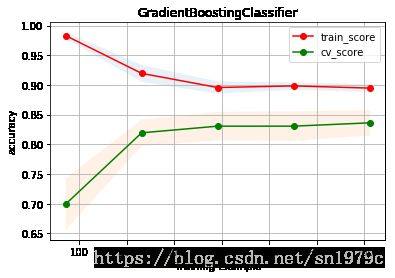
f1 = GradientBoostingClassifier(random_state=2)
# f, axes = plt.subplots(1, 2)
plot_learning_curve(estimater=f1, title='GradientBoostingClassifier', X=train_valid_X, y=train_valid_y, cv=10)
调参
不同的算法会有不同的参数,下面介绍一下常见算法的主要参数。
MLPClassifier:
hidden_layer_sizes :元组格式,长度=n_layers-2, 默认(100,),第i个元素表示第i个隐藏层的神经元的个数。
alpha :float,可选的,默认0.0001,正则化项参数
KNeighborsClassifier:
n_neighbors:该值太小的时候容易过拟合,因此对于该例应该将该值调大
weights:用'distance'则权重与距离成反比,用'uniform'则等权重。
leaf_size:该值越小,建树时间越长
LogisticRegression:
c:正则化系数lambda的倒数,默认为1.0。必须是正浮点型数,越小的数值表示越强的正则化。
class_weight:默认为None即无权重,可以设为"Balance",这时会增加样本量较少的样本的权重。
multi_class:有OvR和MvM两种算法,前者跑得更快,后者精度更高。
GBDT:
n_estimators:决定树数量,太小容易欠拟合,太大容易过拟合,常将其与学习率一起考虑,初始值一般为40-70。
learning_rate:学习率,取值为(0,1],学习率越小越好,但太小了会很慢,一般默认的值是0.1,初始值一般0.05-0.20都可以。
subsample:拟合使用的样本比例,取值为(0,1],选取小于1的值可以防止过拟合,初始值一般用0.8.
max_features:划分时考虑的最大特征数,初始值一般选择总特征数的平方根'sqrt'即可,但还是应该多尝试,最多可以尝试总特征数的30%-40%.
max_depth:决策树最大深度,特征和样本很多时可以限制最大深度。
min_samples_split:内部节点再划分所需最小样本数,避免过拟合,但设定的值过大,可能出现欠拟合现象。这个值应该在总样本数的0.5-1%之间,对不均等分类问题,可以适当调小。
min_samples_leaf:叶子节点最少样本数,样本量很大时,可以增大这个值。
max_leaf_nodes:最大叶子节点数,限制该值可以防止过拟合,具体可以通过交叉验证得到。
GridSearchCV函数会自己生成交叉验证集,因此fit的时候应该用上所有的数据。
我们通过搜索min_samples_split、max_leaf_nodes和max_features来减小过拟合。
paraTest1 = {'max_depth':[None],
"min_samples_split": [2, 4, 6, 8, 10, 12, 14],
'max_leaf_nodes':[3, 5, 7, 9, 11, 13, 15],
'max_features':[6, 8, 10, 12, 14]}
gridSearch1 = GridSearchCV(estimator=GradientBoostingClassifier(random_state=2),
param_grid=paraTest1, scoring='accuracy', cv=5)
gridSearch1.fit(train_valid_X, train_valid_y)
gridSearch1.best_params_, gridSearch1.best_score_
({'max_depth': None,
'max_features': 8,
'max_leaf_nodes': 13,
'min_samples_split': 14},
0.8338945005611672)
接下来试着找到一个较合适的n_estimators和learning_rate的组合,同时调节子样本比例便于降低learning_rate。
paraTest2 = {'n_estimators':[40, 50, 60, 70],
'learning_rate':[0.05, 0.10, 0.15, 0.20],
'subsample':[0.6, 0.7, 0.75, 0.8, 0.85]}
gridSearch2 = GridSearchCV(estimator=gridSearch1.best_estimator_,
param_grid=paraTest2, scoring='accuracy', cv=5)
gridSearch2.fit(train_valid_X, train_valid_y)
gridSearch2.best_params_, gridSearch2.best_score_
({'learning_rate': 0.15, 'n_estimators': 40, 'subsample': 0.7},
0.8395061728395061)
接下来我们成倍地同时减小learning_rate,增大n_estimators,以增强模型的泛化能力,直到得分因此而下降为止。同样的,用多次的分类来减小分类带来的噪声。
注意画learningCurve时cv调得太高标准差会很大。
f = GradientBoostingClassifier(max_depth=None, max_features=8, max_leaf_nodes=13,
min_samples_split=14, learning_rate=0.00375, n_estimators=800, subsample=0.7)
score = 0
estimatorTime = 10
for i in range(estimatorTime):
train_X, valid_X, train_y, valid_y = train_test_split(train_valid_X, train_valid_y, test_size=0.2, random_state=i)
pred = f.fit(train_X,train_y).predict(valid_X)
score += accuracy_score(valid_y, pred)
score /= estimatorTime
print(score)
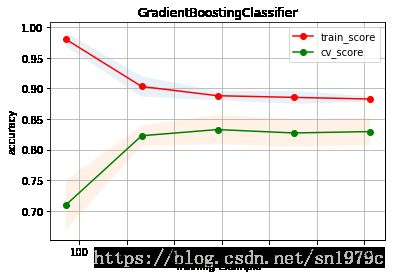
plot_learning_curve(estimater=f, title='GradientBoostingClassifier', X=train_valid_X, y=train_valid_y, cv=5)
0.8178770949720671
预测
f.fit(train_valid_X, train_valid_y)
pred = f.predict(full_X[891:])
submitData['Survived'] =pred
submitData.to_csv('gender_submission.csv', index=False)
importance = pd.DataFrame(f.feature_importances_,
columns=['Importance'],
index=train_valid_X.columns)
importance = importance.sort_values(['Importance'], ascending=False)[0:10]
importance[::-1].plot(kind='barh')
submitData.head()
| PassengerId | Survived | |
|---|---|---|
| 0 | 892 | 0 |
| 1 | 893 | 1 |
| 2 | 894 | 0 |
| 3 | 895 | 0 |
| 4 | 896 | 1 |
得分0.78947,大概在前20%
其他的尝试
减少变量
由于使用全部特征,调参后看学习曲线仍然有些过拟合,因此笔者尝试减少特征数量,用不同的变量再算一次。
笔者直觉上觉得age,Fare,Pclass,Embarked,family几个变量能比较好的解释死亡原因,因此试着只用这些变量来预测。
full_X = pd.concat([family, Pclass, Sex, age, Embarked, fare], axis=1)
# 默认参数预测
train_valid_X = full_X[0:891]
train_valid_y = trainData['Survived']
train_X, valid_X, train_y, valid_y = train_test_split(train_valid_X, train_valid_y, test_size=0.2, random_state=4)
score = np.zeros(9)
classifier = ['DecisionTreeClassifier', 'RandomForestClassifier', 'SVC',
'GradientBoostingClassifier', 'KNeighborsClassifier', 'GaussianNB',
'LogisticRegression', 'ExtraTreesClassifier', 'MLPClassifier']
for i in range(30):
train_X, valid_X, train_y, valid_y = train_test_split(train_valid_X, train_valid_y, test_size=0.2)
model = DecisionTreeClassifier(random_state=random_state).fit(train_X, train_y)
score[0] += accuracy_score(valid_y, model.predict(valid_X))
model = RandomForestClassifier(random_state=random_state, n_estimators=100).fit(train_X, train_y)
score[1] += accuracy_score(valid_y, model.predict(valid_X))
model = SVC().fit(train_X, train_y)
score[2] += accuracy_score(valid_y, model.predict(valid_X))
model = GradientBoostingClassifier(random_state=random_state).fit(train_X, train_y)
score[3] += accuracy_score(valid_y, model.predict(valid_X))
model = KNeighborsClassifier(n_neighbors = 3).fit(train_X, train_y)
score[4] += accuracy_score(valid_y, model.predict(valid_X))
model = GaussianNB().fit(train_X, train_y)
score[5] += accuracy_score(valid_y, model.predict(valid_X))
model = LogisticRegression().fit(train_X, train_y)
score[6] += accuracy_score(valid_y, model.predict(valid_X))
model = ExtraTreesClassifier(random_state=random_state).fit(train_X, train_y)
score[7] += accuracy_score(valid_y, model.predict(valid_X))
model = MLPClassifier(random_state=random_state).fit(train_X, train_y)
score[8] += accuracy_score(valid_y, model.predict(valid_X))
score = score/30
classifierScore = {classifier[i]:score[i] for i in range(len(score))}
classifierScore = pd.Series(classifierScore)
classifierScore.sort_values().plot(kind='barh', xlim=[0.5, 0.85])
plt.ylabel('accuracy')
plt.xlabel('classifier')
Text(0.5,0,'classifier')
paraTest1 = {'max_depth':[None],
"min_samples_split": [2, 4, 6, 8, 10, 12, 14],
'max_leaf_nodes':[3, 5, 7, 9, 11, 13, 15],
'max_features':[2, 4, 6, 8, 10]}
gridSearch1 = GridSearchCV(estimator=GradientBoostingClassifier(random_state=2),
param_grid=paraTest1, scoring='accuracy', cv=5)
gridSearch1.fit(train_valid_X, train_valid_y)
gridSearch1.best_params_, gridSearch1.best_score_
({'max_depth': None,
'max_features': 8,
'max_leaf_nodes': 13,
'min_samples_split': 4},
0.8439955106621774)
paraTest2 = {'n_estimators':[40, 50, 60, 70],
'learning_rate':[0.05, 0.10, 0.15, 0.20],
'subsample':[0.6, 0.7, 0.75, 0.8, 0.85]}
gridSearch2 = GridSearchCV(estimator=gridSearch1.best_estimator_,
param_grid=paraTest2, scoring='accuracy', cv=5)
gridSearch2.fit(train_valid_X, train_valid_y)
gridSearch2.best_params_, gridSearch2.best_score_
({'learning_rate': 0.1, 'n_estimators': 60, 'subsample': 0.7},
0.8439955106621774)
f = GradientBoostingClassifier(max_depth=None, max_leaf_nodes=13,min_samples_split=4, max_features=8,
learning_rate=0.001, n_estimators=3000, subsample=0.7)
score = 0
estimatorTime = 30
for i in range(estimatorTime):
train_X, valid_X, train_y, valid_y = train_test_split(train_valid_X, train_valid_y, test_size=0.2, random_state=i)
pred = f.fit(train_X,train_y).predict(valid_X)
score += accuracy_score(valid_y, pred)
score /= estimatorTime
print(score)
plot_learning_curve(estimater=f, title='GradientBoostingClassifier', X=train_valid_X, y=train_valid_y, cv=5)
0.8318435754189945
f.fit(train_valid_X, train_valid_y)
pred = f.predict(full_X[891:])
submitData['Survived'] =pred
submitData.to_csv('gender_submission.csv', index=False)
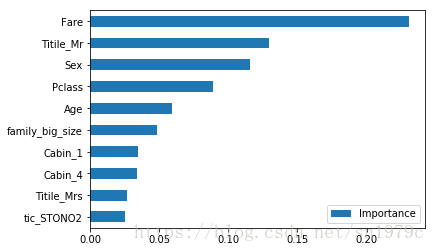
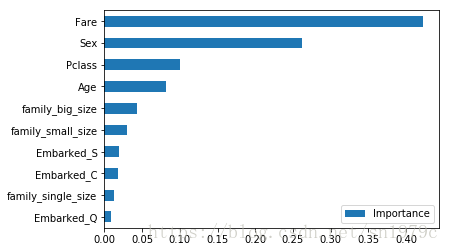
可以看到船费、性别、船舱等级和年龄是你能否在泰坦尼克号活下来的关键因素,这也符合我们之前的分析。
importance = pd.DataFrame(f.feature_importances_,
columns=['Importance'],
index=train_valid_X.columns)
importance = importance.sort_values(['Importance'], ascending=False)
importance[::-1].plot(kind='barh')
submitData.head()
| PassengerId | Survived | |
|---|---|---|
| 0 | 892 | 0 |
| 1 | 893 | 1 |
| 2 | 894 | 0 |
| 3 | 895 | 0 |
| 4 | 896 | 1 |
得分0.79904,准确率上升了约1%,根据learning curve可以看出,过拟合减轻了,训练误差也比之前低了很多,这说明删掉的特征确实是不太好的特征,同时函数的过拟合仍然存在。
在变量构造上继续尝试
笔者继续减少变量,将family改为了family_size。
family_size = full['SibSp'] + full['Parch'] + 1
cabin = full['Cabin']
full_X = pd.concat([cabin, family_size, Pclass, Sex, age, Embarked, fare], axis=1)
# 默认参数预测
train_valid_X = full_X[0:891]
train_valid_y = trainData['Survived']
train_X, valid_X, train_y, valid_y = train_test_split(train_valid_X, train_valid_y, test_size=0.2, random_state=4)
score = np.zeros(9)
classifier = ['DecisionTreeClassifier', 'RandomForestClassifier', 'SVC',
'GradientBoostingClassifier', 'KNeighborsClassifier', 'GaussianNB',
'LogisticRegression', 'ExtraTreesClassifier', 'MLPClassifier']
estimatorTime = 100
for i in range(estimatorTime):
train_X, valid_X, train_y, valid_y = train_test_split(train_valid_X, train_valid_y, test_size=0.2)
model = DecisionTreeClassifier().fit(train_X, train_y)
score[0] += accuracy_score(valid_y, model.predict(valid_X))
model = RandomForestClassifier().fit(train_X, train_y)
score[1] += accuracy_score(valid_y, model.predict(valid_X))
model = SVC().fit(train_X, train_y)
score[2] += accuracy_score(valid_y, model.predict(valid_X))
model = GradientBoostingClassifier().fit(train_X, train_y)
score[3] += accuracy_score(valid_y, model.predict(valid_X))
model = KNeighborsClassifier().fit(train_X, train_y)
score[4] += accuracy_score(valid_y, model.predict(valid_X))
model = GaussianNB().fit(train_X, train_y)
score[5] += accuracy_score(valid_y, model.predict(valid_X))
model = LogisticRegression().fit(train_X, train_y)
score[6] += accuracy_score(valid_y, model.predict(valid_X))
model = ExtraTreesClassifier().fit(train_X, train_y)
score[7] += accuracy_score(valid_y, model.predict(valid_X))
model = MLPClassifier().fit(train_X, train_y)
score[8] += accuracy_score(valid_y, model.predict(valid_X))
score = score/estimatorTime
classifierScore = {classifier[i]:score[i] for i in range(len(score))}
classifierScore = pd.Series(classifierScore)
classifierScore.sort_values().plot(kind='barh', xlim=[0.5, 0.85])
plt.ylabel('accuracy')
plt.xlabel('classifier')
Text(0.5,0,'classifier')
paraTest1 = {'max_depth':[None],
"min_samples_split": [2, 4, 6, 8, 10, 12, 14],
'max_leaf_nodes':[3, 5, 7, 9, 11, 13, 15],
'max_features':[2, 4, 6]}
gridSearch1 = GridSearchCV(estimator=GradientBoostingClassifier(random_state=2),
param_grid=paraTest1, scoring='accuracy', cv=5)
gridSearch1.fit(train_valid_X, train_valid_y)
gridSearch1.best_params_, gridSearch1.best_score_
({'max_depth': None,
'max_features': 4,
'max_leaf_nodes': 13,
'min_samples_split': 14},
0.8327721661054994)
paraTest2 = {'n_estimators':[40, 50, 60, 70],
'learning_rate':[0.05, 0.10, 0.15, 0.20],
'subsample':[0.6, 0.7, 0.75, 0.8, 0.85]}
gridSearch2 = GridSearchCV(estimator=gridSearch1.best_estimator_,
param_grid=paraTest2, scoring='accuracy', cv=5)
gridSearch2.fit(train_valid_X, train_valid_y)
gridSearch2.best_params_, gridSearch2.best_score_
({'learning_rate': 0.1, 'n_estimators': 70, 'subsample': 0.85},
0.835016835016835)
f = GradientBoostingClassifier(max_depth=None, max_leaf_nodes=11,min_samples_split=10, max_features=6,
learning_rate=0.001, n_estimators=2500, subsample=0.7)
score = 0
estimatorTime = 30
for i in range(estimatorTime):
train_X, valid_X, train_y, valid_y = train_test_split(train_valid_X, train_valid_y, test_size=0.2, random_state=i)
pred = f.fit(train_X,train_y).predict(valid_X)
score += accuracy_score(valid_y, pred)
score /= estimatorTime
print(score)
plot_learning_curve(estimater=f, title='GradientBoostingClassifier', X=train_valid_X, y=train_valid_y, cv=5)
0.8256983240223462
过拟合减轻了,但这是以训练得分下降为代价的,交叉验证集的得分没什么变化,看上去没有之前跑的好
用多层的预测器堆叠预测
不同的预测器所关注的变量不一样,用多层预测器堆叠预测可以综合各个预测器的效果。
full_X = pd.concat([family, Pclass, Sex, age, Embarked, fare], axis=1)
# 默认参数预测
train_valid_X = full_X[0:891]
train_valid_y = trainData['Survived']
train_X, valid_X, train_y, valid_y = train_test_split(train_valid_X, train_valid_y, test_size=0.2, random_state=4)
选取准确率较高的七个预测器
DTC = DecisionTreeClassifier()
adaDTC = AdaBoostClassifier(DTC, random_state=7)
ada_param_grid = {"base_estimator__criterion" : ["gini", "entropy"],
"base_estimator__splitter" : ["best", "random"],
"algorithm" : ["SAMME","SAMME.R"],
"n_estimators" :[1, 3, 10, 30, 100, 300],
"learning_rate": [0.0001, 0.001, 0.01, 0.1, 1]}
gsadaDTC = GridSearchCV(adaDTC,param_grid = ada_param_grid, cv=5, scoring="accuracy", n_jobs= 4)
gsadaDTC.fit(train_valid_X,train_valid_y)
ada_best = gsadaDTC.best_estimator_
gsadaDTC.best_score_
0.8316498316498316
ExtC = ExtraTreesClassifier()
## Search grid for optimal parameters
ex_param_grid = {"max_depth": [None],
"max_features": [2, 4, 6],
"min_samples_split": [2, 3, 7, 10, 13],
"min_samples_leaf": [1, 3, 10],
"bootstrap": [False],
"n_estimators" :[100,300],
"criterion": ["gini"]}
gsExtC = GridSearchCV(ExtC,param_grid = ex_param_grid, cv=5, scoring="accuracy", n_jobs= 4)
gsExtC.fit(train_X,train_y)
ExtC_best = gsExtC.best_estimator_
# Best score
gsExtC.best_score_
0.8174157303370787
RFC = RandomForestClassifier()
## Search grid for optimal parameters
rf_param_grid = {"max_depth": [None],
"max_features": [2, 4, 6],
"min_samples_split": [2, 3, 10],
"min_samples_leaf": [1, 3, 10],
"bootstrap": [False],
"n_estimators" :[100,300],
"criterion": ["gini"]}
gsRFC = GridSearchCV(RFC,param_grid = rf_param_grid, cv=5, scoring="accuracy", n_jobs= 4)
gsRFC.fit(train_valid_X,train_valid_y)
RFC_best = gsRFC.best_estimator_
# Best score
gsRFC.best_score_
0.8338945005611672
GBC = GradientBoostingClassifier()
gb_param_grid = {'loss' : ["deviance"],
'n_estimators' : [100,200,300],
'learning_rate': [0.1, 0.05, 0.01],
'max_depth': [4, 8],
'min_samples_leaf': [1, 3, 10, 30, 100,150],
'max_features': [2, 4, 6]
}
gsGBC = GridSearchCV(GBC,param_grid = gb_param_grid, cv=5, scoring="accuracy", n_jobs= 4)
gsGBC.fit(train_valid_X,train_valid_y)
GBC_best = gsGBC.best_estimator_
# Best score
gsGBC.best_score_
0.8406285072951739
SVMC = SVC(probability=True)
svc_param_grid = {'kernel': ['rbf'],
'gamma': [ 0.001, 0.01, 0.1, 1],
'C': [1, 10, 50, 100,200,300, 1000]}
gsSVMC = GridSearchCV(SVMC,param_grid = svc_param_grid, cv=5, scoring="accuracy", n_jobs= 4)
gsSVMC.fit(train_valid_X, train_valid_y)
SVMC_best = gsSVMC.best_estimator_
# Best score
gsSVMC.best_score_
0.8282828282828283
LGR = LogisticRegression()
lgr_param_grid = {'C': [0.1, 0.3, 0.01, 0.03, 1, 3, 10, 30, 100]}
gsLGR = GridSearchCV(LGR,param_grid = lgr_param_grid, cv=5, scoring="accuracy", n_jobs= 4)
gsLGR.fit(train_valid_X, train_valid_y)
LGR_best = gsLGR.best_estimator_
# Best score
gsLGR.best_score_
0.8181818181818182
KNB = KNeighborsClassifier()
knb_param_grid = {'n_neighbors': [1, 3, 5, 7, 10, 13, 15, 17, 20, 30]}
gsKNB = GridSearchCV(KNB,param_grid = knb_param_grid, cv=5, scoring="accuracy", n_jobs= 4)
gsKNB.fit(train_valid_X, train_valid_y)
KNB_best = gsKNB.best_estimator_
# Best score
gsKNB.best_score_
0.8226711560044894
[('rfc', RFC_best), ('extc', ExtC_best),
('svc', SVMC_best), ('adac',ada_best),('gbc',GBC_best)]
class stackClassifier:
def __init__(self, estimators):
self.estimators = estimators
self.layer2 = 0
def fit(self, x, y):
layer1_x = pd.DataFrame()
layer1_y = y
for i in range(len(self.estimators)):
self.estimators[i] = self.estimators[i].fit(x, y)
layer1_x[str(i)] = self.estimators[i].predict(x)
# param_grid = {"max_depth": [None],
# "max_features": [1, 3, 5],
# "min_samples_split": [2, 3, 10],
# "min_samples_leaf": [1, 3, 10],
# "bootstrap": [False],
# "n_estimators" :[100,300],
# "criterion": ["gini"]}
# gs = GridSearchCV(RandomForestClassifier(),param_grid = param_grid, cv=5, scoring="accuracy", n_jobs= 4)
# gs.fit(x,y)
# best = gs.best_estimator_
# self.layer2 = RandomForestClassifier(n_estimators=100).fit(layer1_x, layer1_y)
self.layer2 = MLPClassifier(hidden_layer_sizes=(96,)).fit(layer1_x, layer1_y)
return self
def predict(self, x):
layer1_x = pd.DataFrame()
for i in range(len(self.estimators)):
layer1_x[str(i)] = self.estimators[i].predict(x)
pred = self.layer2.predict(layer1_x)
return pred
def get_params(self):
return self.layer2.get_params
f = []
f.append(DecisionTreeClassifier())
f.append(RFC_best)
f.append(SVMC_best)
f.append(GBC_best)
f.append(KNB_best)
f.append(LGR_best)
f.append(ExtC_best)
score = 0
for i in range(30):
train_X, valid_X, train_y, valid_y = train_test_split(train_valid_X, train_valid_y, test_size=0.2, random_state=i**2)
estimator = stackClassifier(f).fit(train_X, train_y)
pred = estimator.predict(valid_X)
score += accuracy_score(valid_y, pred)
score /= 30
print(score)
0.8175046554934825
用所有变量预测提交准确率:0.79425
用较少变量预测提交准确率:0.80382
决策树是个好算法
在提交过程中笔者发现单用决策树分类的效果非常好,这可能是因为复杂的模型反而会过拟合。用较少变量加上决策树的默认参数就能达到top5%的排名。
score = 0
estimatorTime = 10000
for i in range(estimatorTime):
train_X, valid_X, train_y, valid_y = train_test_split(train_valid_X, train_valid_y, test_size=0.2)
pred = DecisionTreeClassifier().fit(train_X, train_y).predict(valid_X)
score += accuracy_score(valid_y, pred)
score /= estimatorTime
print(score)
0.8245324022346556
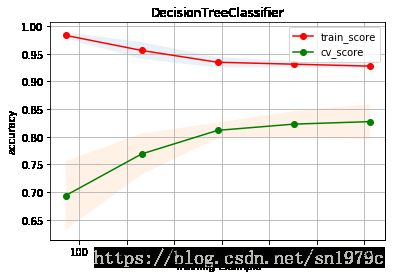
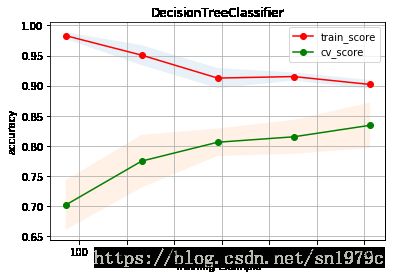
plot_learning_curve(estimater=DecisionTreeClassifier(), title='DecisionTreeClassifier', X=train_valid_X, y=train_valid_y, cv=5)
DCT = DecisionTreeClassifier()
dct_param_grid = {'max_depth': [4, 6, 8, 10, 12],
'min_samples_leaf': [1, 3, 10, 30],
'min_samples_split': [2, 3, 5, 7, 10, 13, 15, 17]}
gsDCT = GridSearchCV(DCT,param_grid = dct_param_grid, cv=5, scoring="accuracy", n_jobs= 4)
gsDCT.fit(train_valid_X, train_valid_y)
DCT_best = gsDCT.best_estimator_
# Best score
gsDCT.best_score_
0.835016835016835
gsDCT.best_params_
{'max_depth': 10, 'min_samples_leaf': 1, 'min_samples_split': 2}
score = 0
estimatorTime = 10000
for i in range(estimatorTime):
train_X, valid_X, train_y, valid_y = train_test_split(train_valid_X, train_valid_y, test_size=0.2)
pred = DCT_best.fit(train_X, train_y).predict(valid_X)
score += accuracy_score(valid_y, pred)
score /= estimatorTime
print(score)
0.8285536312849319
plot_learning_curve(estimater=DCT_best, title='DecisionTreeClassifier', X=train_valid_X, y=train_valid_y, cv=5)
pred = DCT_best.fit(train_valid_X, train_valid_y).predict(full_X[891:])
submitData['Survived'] = pred
submitData.to_csv('gender_submission.csv', index=False)
致谢
感谢课程老师的教导,感谢kaggler们在讨论区分享自己的思路,有时间我也会将这份notebook翻译成英语放到讨论区。
在做这个练习赛的过程中,我参考了下列文献:
http://www.cnblogs.com/pinard/p/6143927.html
https://www.kaggle.com/helgejo/an-interactive-data-science-tutorial
https://www.kaggle.com/yassineghouzam/titanic-top-4-with-ensemble-modeling/comments#latest-402440
https://www.kaggle.com/ash316/eda-to-prediction-dietanic/comments#latest-401373
https://blog.csdn.net/han_xiaoyang/article/details/52663170
有趣的事实
这份notebook写了很久,泰坦尼克上人们的各个特征和存活率令人惊讶。
为什么JACK死了而ROSE活着?这并不是偶然,男性的存活率仅为20%,而女性的存活率为80%,身为女性且来自头等舱的ROSE存活率高达95%,身为男性且来自二等舱的Jack存活率不足10%,悲剧似乎在他们上船的那一刻就已经注定了。