DARTS-:增加辅助跳连,走出搜索性能崩溃
DARTS-:增加辅助跳连,走出搜索性能崩溃
-
-
- 摘要
- Skip-Connect富集的两重原因
- 方法
- 结果
-
- CIFAR-10 和 ImageNet
- NAS-Bench-201
-
本文是由美团,上交,小米,中科院联合发表的可微分神经网络架构搜索的文章,名为DARTS-。本文主要是解决skip-connect富集导致的训练不稳定问题。本文证明了跳连与其他候选操作相比具有明显的优势,它可以很容易地从劣势状态中恢复过来并成为主导,并提出用辅助跳过连接来剔除这种优势,确保所有操作的竞争更加公平。
- 文章题目:DARTS-: robustly stepping out of performance collapse without indicators
- 文章链接:https://arxiv.org/pdf/2009.01027.pdf
- ICLR 2021 OpenReview : https://openreview.net/forum?id=KLH36ELmwIB
摘要
尽管可微分架构搜索(DARTS)发展迅速,但它长期存在性能不稳定的问题,这极大地限制了它的应用。现有的鲁棒性方法是从由此产生的恶化行为中获取线索,而不是找出其原因。各种指标如海森特征值等被提出来作为性能崩溃前停止搜索的信号。然而,如果阈值设置不当,这些基于指标的方法往往很容易拒绝好的架构,更何况搜索是内在的噪声。在本文中,进行了一种更细微更直接的方法来解决塌陷问题。本文首先证明了跳连与其他候选操作相比具有明显的优势,它可以很容易地从劣势状态中恢复过来并成为主导。因此,本文提出用辅助跳过连接来剔除这种优势,确保所有操作的竞争更加公平,在各种数据集上的大量实验验证了它可以大幅提高鲁棒性。
Skip-Connect富集的两重原因
提出skip-connect操作是在ResNet中构造残差块的方法,这大大提高了训练的稳定性。 只需将它们堆叠起来,甚至可以将网络加深到数百层,而不会降低精度。 相反,当网络变得更深时,堆叠普通的VGG块会降低性能。
从梯度流的角度来看,skip-connect操作可以缓解梯度消失的问题。 给定n个残差块的堆栈,可以将第(i + 1)个残差块 X i + 1 X_{i+1} Xi+1的输出计算为:
X i + 1 = f i + 1 ( X i , W i + 1 ) + X i X_{i+1}=f_{i+1}\left(X_{i}, W_{i+1}\right)+X_{i} Xi+1=fi+1(Xi,Wi+1)+Xi
其中 f i + 1 f_{i+1} fi+1表示权重 W i + 1 W_{i+1} Wi+1与第(i + 1)个残差块的运算。 假设模型的损失函数为L,则 X i X_i Xi的梯度可按以下方式获得( 1 \mathbb{1} 1表示所有项均为1的张量):
∂ L ∂ X i = ∂ L ∂ X i + 1 ⋅ ( ∂ f i + 1 ∂ X i + 1 ) = ∂ L ∂ X i + j ⋅ ∏ k = 1 j ( ∂ f i + k ∂ X i + k − 1 + 1 ) \frac{\partial \mathcal{L}}{\partial X_{i}}=\frac{\partial \mathcal{L}}{\partial X_{i+1}} \cdot\left(\frac{\partial f_{i+1}}{\partial X_{i}}+\mathbb{1}\right)=\frac{\partial \mathcal{L}}{\partial X_{i+j}} \cdot \prod_{k=1}^{j}\left(\frac{\partial f_{i+k}}{\partial X_{i+k-1}}+\mathbb{1}\right) ∂Xi∂L=∂Xi+1∂L⋅(∂Xi∂fi+1+1)=∂Xi+j∂L⋅k=1∏j(∂Xi+k−1∂fi+k+1)
根据公式可以观察到,浅层的梯度始终包括深层的梯度,这减轻了 W i W_i Wi的梯度消失。
∂ L ∂ W i = ∂ L ∂ X i + j ⋅ ∏ k = 1 j ( ∂ f i + k ∂ X i + k − 1 + 1 ) ⋅ ∂ f i ∂ W i \frac{\partial \mathcal{L}}{\partial W_{i}}=\frac{\partial \mathcal{L}}{\partial X_{i+j}} \cdot \prod_{k=1}^{j}\left(\frac{\partial f_{i+k}}{\partial X_{i+k-1}}+\mathbb{1}\right) \cdot \frac{\partial f_{i}}{\partial W_{i}} ∂Wi∂L=∂Xi+j∂L⋅k=1∏j(∂Xi+k−1∂fi+k+1)⋅∂Wi∂fi
为了分析skip-connect操作如何影响残留网络的性能,本文在ResNet中的所有跳过连接上引入了可训练的系数 β 。 因此, X i X_i Xi的斜率转换为:
∂ L ∂ X i = ∂ L ∂ X i + 1 ⋅ ( ∂ f i + 1 ∂ X i + β ) \frac{\partial \mathcal{L}}{\partial X_{i}}=\frac{\partial \mathcal{L}}{\partial X_{i+1}} \cdot\left(\frac{\partial f_{i+1}}{\partial X_{i}}+\beta\right) ∂Xi∂L=∂Xi+1∂L⋅(∂Xi∂fi+1+β)
如果 β < 1 ,则在向浅层的反向传播(BP)期间,深层的梯度逐渐消失。这里 β 控制 BP 中梯度的记忆以稳定训练过程。
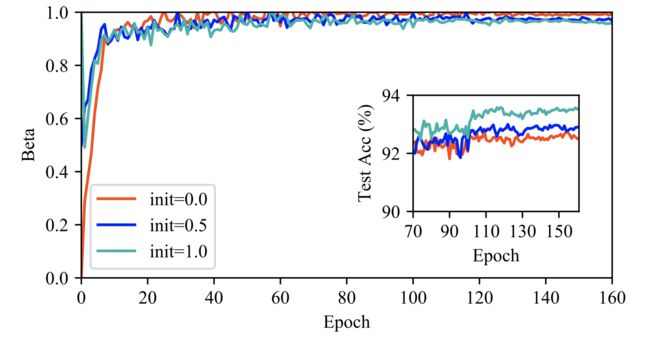
本文在ResNet50上进行了验证性实验,并在下图中显示了结果。通过用{0,0.5,1.0}初始化β,可以直观地了解 β 随训练时期的变化趋势。 我们观察到,不管初始化如何,β 在 40 个周期后都收敛到 1 ,这表明残差结构学会了将 β 推到一个相当大的值以缓解梯度消失。
同样,DARTS 利用可训练参数 β s k i p \beta_{skip} βskip 来表示跳过连接的重要性。 但是,在搜索阶段, β s k i p \beta_{skip} βskip 通常可以增加并控制体系结构参数,最终导致性能下降。 本文分析了DARTS中的大 β s k i p \beta_{skip} βskip 可能来自两个方面:一方面,当超网自动学习以减轻梯度消失时,它将 β s k i p \beta_{skip} βskip 推至适当的大值; 另一方面,跳过连接的确是目标网络的重要连接,应在离散化阶段选择该连接。 因此,DARTS中的跳过连接起着双重作用:作为稳定超网训练的辅助连接,以及作为构建最终网络的候选操作。 受以上观察和分析的启发,本文建议通过区分跳过连接和处理梯度流的两个作用来稳定搜索过程。
方法
为了区分 skip-connect 这两个角色,本文在一个单元的每两个节点之间引入一个辅助跳过连接,如下图:
一方面,即使 β s k i p \beta_{skip} βskip很小,固定的辅助跳过连接也具有稳定超网训练的功能。 另一方面,它也打破了不公平的优势,因为残差块的有利贡献被排除了。 因此,所学习的体系结构参数 β s k i p \beta_{skip} βskip可以摆脱控制梯度记忆的作用,并且更精确地旨在表示跳过连接作为候选操作的相对重要性。
传统的DARTS节点操作表示为:
o ˉ ( i , j ) ( x ) = ∑ o ∈ O exp ( α o ( i , j ) ) ∑ o ′ ∈ O exp ( α o ′ ( i , j ) ) o ( x ) \bar{o}^{(i, j)}(x)=\sum_{o \in \mathcal{O}} \frac{\exp \left(\alpha_{o}^{(i, j)}\right)}{\sum_{o^{\prime} \in \mathcal{O}} \exp \left(\alpha_{o^{\prime}}^{(i, j)}\right)} o(x) oˉ(i,j)(x)=o∈O∑∑o′∈Oexp(αo′(i,j))exp(αo(i,j))o(x)
加入辅助跳过连接,输出特征图的节点可以重新表达为:
o ˉ ( i , j ) ( x ) = β x + ∑ o ∈ O β o ( i , j ) o ( x ) = ( β + β s k i p ( i , j ) ) x + ∑ o ≠ s k i p β o ( i , j ) o ( x ) \bar{o}^{(i, j)}(x)=\beta x+\sum_{o \in \mathcal{O}} \beta_{o}^{(i, j)} o(x)=\left(\beta+\beta_{s k i p}^{(i, j)}\right) x+\sum_{o \neq s k i p} \beta_{o}^{(i, j)} o(x) oˉ(i,j)(x)=βx+o∈O∑βo(i,j)o(x)=(β+βskip(i,j))x+o=skip∑βo(i,j)o(x)
其中, β o i , j = exp ( α o ( i , j ) ) ∑ o ′ ∈ O exp ( α o ′ ( i , j ) ) \beta_{o}^{i, j}=\frac{\exp \left(\alpha_{o}^{(i, j)}\right)}{\sum_{o^{\prime} \in \mathcal{O}} \exp \left(\alpha_{o^{\prime}}^{(i, j)}\right)} βoi,j=∑o′∈Oexp(αo′(i,j))exp(αo(i,j))表示各操作的平均重要程度, β \beta β 是独立于架构参数的系数。
加入辅助跳过连接后是如何处理梯度流问题的呢?首先,根据论文《Theory-inspired path-regularized differential network architecture search》指出超网络中网络权重 W 的收敛在很大程度上取决于 β s k i p \beta_{skip} βskip。 具体而言,假设搜索空间中仅包括三个操作(无,跳过连接和卷积),MSE作训练损失函数。 当固定架构参数 β o ( i , j ) \beta_{o}^{(i, j)} βo(i,j)以通过梯度下降优化 W 时,训练损失可以一步降低(1-ηλ/4)比率,并且概率至少为 1-δ ,其中 η 是学习率由δ限定,λ 公式如下:
λ ∝ ∑ i = 0 h − 2 [ ( β c o n v ( i , h − 1 ) ) 2 ∏ t = 0 i − 1 ( β s k i p ( t , i ) ) 2 ] \lambda \propto \sum_{i=0}^{h-2}\left[\left(\beta_{c o n v}^{(i, h-1)}\right)^{2} \prod_{t=0}^{i-1}\left(\beta_{s k i p}^{(t, i)}\right)^{2}\right] λ∝i=0∑h−2[(βconv(i,h−1))2t=0∏i−1(βskip(t,i))2]
其中,h是超网的层数。 从上面等式可以看出,λ 比 β c o n v \beta_{conv} βconv更依赖于 β s k i p \beta_{skip} βskip,这表明网络权重 W 可以在较大的 β s k i p \beta_{skip} βskip 情况下更快收敛。 但是,通过包含权重为 β 的辅助跳过连接,上面的公式可以细化如下:
λ ∝ ∑ i = 0 h − 2 [ ( β c o n v ( i , h − 1 ) ) 2 ∏ t = 0 i − 1 ( β s k i p ( t , i ) + β ) 2 ] \lambda \propto \sum_{i=0}^{h-2}\left[\left(\beta_{c o n v}^{(i, h-1)}\right)^{2} \prod_{t=0}^{i-1}\left(\beta_{s k i p}^{(t, i)}+\beta\right)^{2}\right] λ∝i=0∑h−2[(βconv(i,h−1))2t=0∏i−1(βskip(t,i)+β)2]
其中 β ≫ β s k i p \beta \gg \beta_{s k i p} β≫βskip 使 λ 对 β s k i p \beta_{skip} βskip 不敏感,因此网络权重 W 的收敛更多地取决于 β c o n v \beta_{c o n v} βconv。 在搜索开始时, β s k i p \beta_{skip} βskip的值为0.15,而 β 为1.0。 从收敛定理的观点来看,辅助跳过连接减轻了 β s k i p \beta_{skip} βskip 的特权,并使架构参数之间的竞争均等。 即使当 β 逐渐衰减时,由于网络权重W已收敛到最佳点,因此公平竞争仍然成立。 所以,DARTS-能够稳定DARTS的搜索阶段。
结果
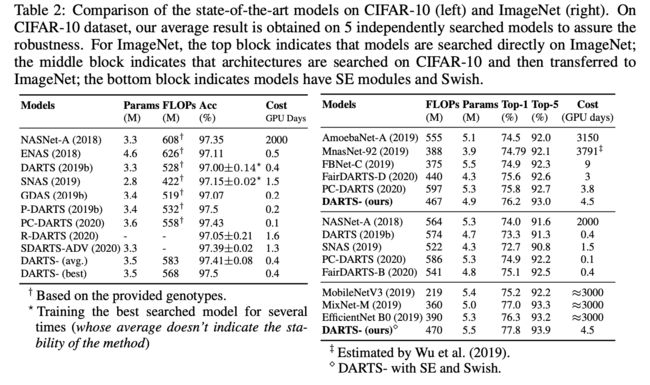
CIFAR-10 和 ImageNet
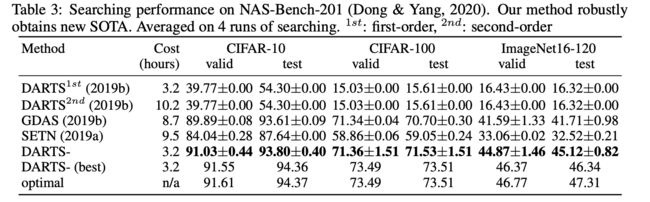
NAS-Bench-201
![]()