聚类数目的多种确定方法与理论证明

前言

上一篇文章我们主要是自己实现了kmeans++算法的底层逻辑，并用于实际数据来筛选异常值。之前也略微提到过，使用聚类模型有个很重要的步骤就是如何开始确定聚类中心的个数，这无论是划分聚类还是层次聚类等，都会涉及的问题，接下来我们就此问题展开讨论。

岁月如云，匪我思存，写作不易，望路过的朋友们点赞收藏加关注哈，在此表示感谢！
本人的知乎平台欢迎参观交流

一：确定聚类中心数目的基础方法

• 肘方法

此方法很容易理解和实现，大致意思就是计算每一个聚类数目下的点跟对应的聚类中心的误差平方和（SSE），那么每选则不同的聚类数目都有不同的SSE，聚类数目越多，SSE必然会小，试想一下，如果所有点都是聚类中心，可想而知SSE=0。
我们定义SSE计算公式如下：
$SSE={\sum }_{i=1}^k{\sum }_{j\in C_i}|j-m_i{|}^2$
公式中要注意 $m_i$ 是第个 $i$ 类的聚类中心， $j$ 是属于第$i$ 类数据点的，并不是所有点跟所有聚类中心做距离运算，不然的话SSE不会随聚类数目的增加而趋于0。
既然我们知道SSE随聚类数目增加而趋于0，这中间过程就会存在下降速率大的一段，而且聚类数目越往后增大，下降速率会趋于平稳，那么我们一般会选择最陡峭的一段的末端值作为真实聚类数目。

• 轮廓系数

轮廓系数（Silhouette Coefficient）也是效果好坏的一种评价方式，它结合内聚度和分离度两种因素。可以用来在相同原始数据的基础上用来评价不同算法、或者算法不同运行方式对聚类结果所产生的影响。具体实现跟如下几个量有关：
$S(i)=\frac{b(i)-a(i)}{max\{a(i),b(i)\}}$ ，具体什么意思呢？
其中 $a(i)$ 意思是点 $i$ 到所有它在的聚类簇中其它点的距离的平均值； $b(i)$ 是点 $i$到某一个包含它的聚类簇内的所有点的平均值的最小值。我们从如下图1可以清楚的了解如上所说的这一过程。
所以从公式分母可知， $S(i)$ 取值必定属于 $(-1,1)$ ，且越接近1代表内聚度和分离度越优。

图1：来源于百度百科

• Calinski Harabasz值

CH值具体公式如下：
$CH(k)=\frac{trB(k)/(k-1)}{trW(k)/(n-k)}$ ，公式中我们特别说明 $n$ 表示聚类数目，$k$ 表示当前的聚类数目， $trB(k)$ 表示类与类之间的离差矩阵的迹， $trW(k)$ 表示类内离差矩阵的迹。这里的公式具体不展开叙述了，有兴趣的可以参考文章如下。

A dendrite method for cluster analysis

CH值同样也是数值越大，聚类的数目就越优。

二：方法修正

• 蒙特卡洛方法取期望避免出现局部最优情况

在上一篇文章我们提到，基于k-means或者k-means++算法会陷入局部最优情况，也许还没迭代几次，聚类中心就不更新了，那么通过上面所叙述的3种方法算出来的值每次结果定会有所波动，这种情况除了从算法底层角度加以修正外，也可以从统计角度出发，那就是多次运行结果取均值，最终选择值最大或者下降速率最大的点的位置。

• 基础方法的组合

通过取均值得来的数值后，我们可以把上述方法的结果组合起来观察，在满足簇内越“聚拢”的情况，也想簇间越“分离”。

三：实验内容

• “震荡”阶段的实验内容

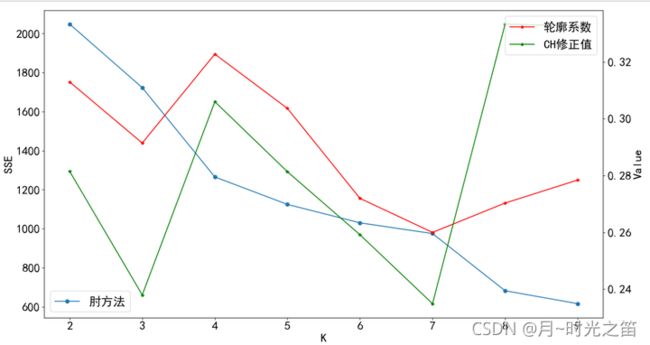
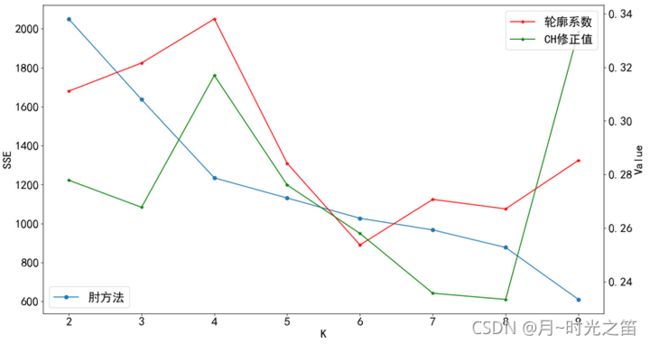
为了验证我们我们修正方法的有效，我们先单次运行程序看看如何

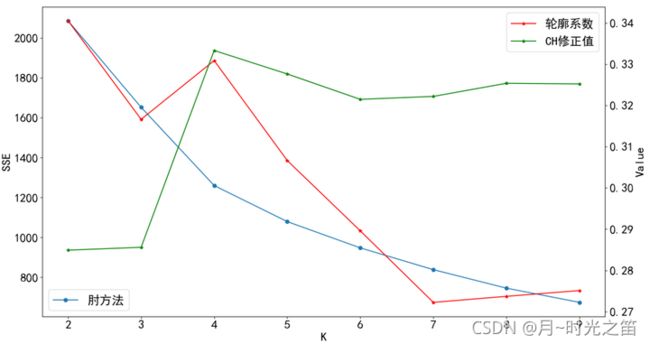
注：由于CH值和轮廓系数值存在很大的数量差异，我们对CH值进行修正压缩后，放入第二坐标系中

图2

图3

图4

从图2，图3，图4中，我们发现轮廓系数、CH修正值、肘方法的表现相当的“不稳定”，一会儿在 $k=3$ 达到最大，一会在 $k=4$ 达到最大。。。。对这些指标进行组合判断，也难判断出哪个聚类数目是最优的，于是我们需要对这些指标进行重复蒙特卡洛循环取均值观察实验结果如何。

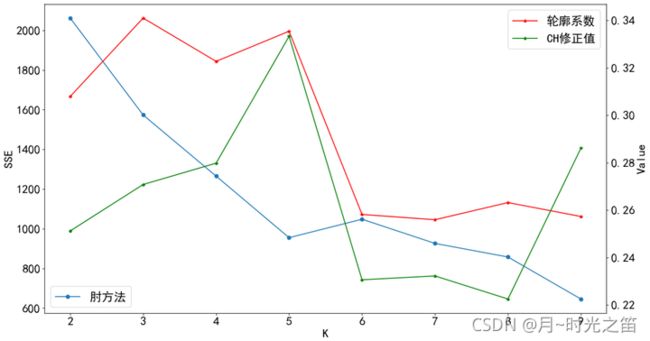
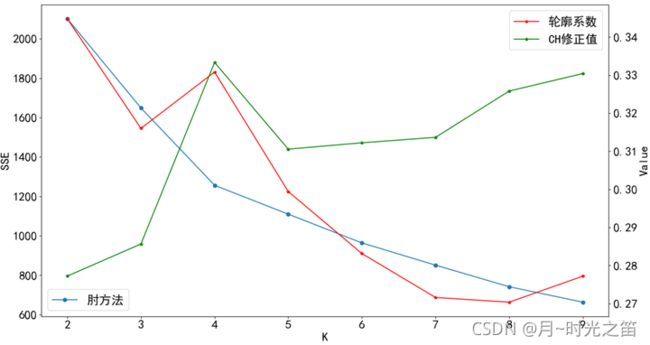
• 蒙特卡洛循环取均值观察实验结果

图5

图6

从上述图5和图6我们可以清楚地发现，经过多次循环后，所有的指标数据表现走向“平稳”，不再出现无规律的“震荡”，在 $k=4$ 时，所有的指标数据综合下是达到最优的状态，即肘方法在 $k=4$ 时是下降最快的一段的末端点，CH修正值达到最大，尽管轮廓系数不是最大，但明显是第2优的位置，跟最大的差别也不是很大，所以最终我们确定最佳聚类的数目为4。

• 代码参考

对于SSE的计算我们先定义函数

def SSE_clu(v1,v2):
    return sum(np.power(v1 - v2,2))

接在再具体设计计算相关指标数据函数，这里肘方法我们通过自己定义方法实现，轮廓系数和CH值的大致逻辑如出一辙，也是比较容易实现的，我们就直接调用相关函数。

这里的K_means不是普通的kmeans函数，对应的是上一篇文章中我们自己实现的K-means++函数，详细参考上篇文章

上篇文章链接

def evaluate_func(data_norm,data_matx):
    ls_k = [2,3,4,5,6,7,8,9]
    ls_sil = []
    ls_ch = []
    ls_elbows =[]
    for i in ls_k:
        ls_elbow = []
        R = K_means(data_matx, i, get_cent_value(data_matx, i))###聚类的输出结果
        res1 = R[0].T.tolist()[0]###输出的是聚类类比
        res2 = R[1]##输出的是聚类中心
        for j in data_st.index:
            choose_label = res2[int(res1[j - 1]), :].tolist()[0]
            sse = SSE_clu(data_st.iloc[j - 1, :], choose_label)##肘方法
            ls_elbow.append(sse)
        ls_sil.append(metrics.silhouette_score(data_norm,res1))###轮廓系数
        ls_ch.append(metrics.calinski_harabasz_score(data_norm,res1))###CH值
        ls_elbows.append(sum(ls_elbow))
    return ls_elbows,ls_sil,ls_ch,len(ls_k)
R_e = evaluate_func(data_st,data_temp)

最后定义蒙特卡洛函数如下：

def monte_carlo(epochs=20):
    matx_elbows = np.mat(np.zeros((epochs,R_e[3])))
    matx_sil = np.mat(np.zeros((epochs, R_e[3])))
    matx_ch = np.mat(np.zeros((epochs, R_e[3])))
    for i in range(epochs):
        Repoch = evaluate_func(data_st,data_temp)
        matx_elbows[i, :] = Repoch[0]
        matx_sil[i, :] = Repoch[1]
        matx_ch[i, :] = Repoch[2]

    mean_elbows = matx_elbows.sum(axis=0) / epochs
    mean_sil = matx_sil.sum(axis=0) / epochs
    mean_ch = matx_ch.sum(axis=0) / epochs
    mean_ch_norm = mean_ch / max(mean_ch.tolist()[0]) / 3

    print('SSE',mean_elbows.tolist()[0])
    print('轮廓系数',mean_sil.tolist()[0])
    print('CH值',mean_ch.tolist()[0])
    print('0-1标准化CH值',mean_ch_norm.tolist()[0])
    # plt.figure(figsize=(15,8))

    fig = plt.figure(figsize=(15, 8))
    ax1 = fig.add_subplot(1, 1, 1)
    ax2 = ax1.twinx()
    X = range(2, R_e[3] + 2)
    ax1.plot(X, mean_elbows.tolist()[0], marker='o', label='肘方法')
    ax2.plot(X, mean_sil.tolist()[0], 'r', marker='*', label='轮廓系数')
    ax2.plot(X, mean_ch_norm.tolist()[0], 'g', marker='*', label='CH修正值')
    ax1.set_ylabel('SSE', fontsize=20)
    ax1.set_xlabel('K', fontsize=20)
    ax2.set_ylabel('Value', fontsize=20)
    ax1.tick_params(labelsize=20)
    ax2.tick_params(labelsize=20)
    ax1.legend(loc='lower left', fontsize=20)
    ax2.legend(loc='upper right',fontsize=20)
    plt.show()
monte_carlo(epochs=30)

四：关于蒙特卡洛方法的有效性证明

设聚类数目取值一直到 $m（m<\infty ）$，每次独立循环 m 个聚类数目 n 次，每个聚类数目之间独立，设第 i 个聚类存在波动 $d_i>0$ ，且每个波动值是有界的，定义

$D(C_i)=d_i(1<i<m,D\in R^m)$,
那么 $m$ 个一起整体有

$D\left({\sum }_{k=1}^m{C}_k\right)={\sum }_{k=1}^m{d}_k$ ,

接着独立循环 n 次中的第 k 个聚类数目的平均波动值为

$D(C_{kn})=\frac{d_{k1}+d_{k2}+...+d_{kn}}{n}=\frac{1}{n}{\sum }_{j=1}^n{d}_{kj}$(1) ,

那么 $m$ 个一起整体有

$D\left({\sum }_{k=1}^m{C}_{kn}\right)=D\left(\frac{1}{n}{\sum }_{j=1}^n{\sum }_{k=1}^m{C}_{kj}\right)$ ,

由独立方差性质（两两变量之间的协方差为0）有

$D\left({\sum }_{k=1}^m{C}_{kn}\right)=\frac{1}{n^2}D\left({\sum }_{j=1}^n{\sum }_{k=1}^m{C}_{kj}\right)=\frac{1}{n^2}D\left({\sum }_j^n{C}_{1j}\right)+\frac{1}{n^2}D\left({\sum }_j^n{C}_{2j}\right)+...+\frac{1}{n^2}D\left({\sum }_j^n{C}_{mj}\right)$(2)

那么我们只要证明出

$D\left({\sum }_{k=1}^m{C}_{kn}\right)<D\left({\sum }_{k=1}^m{C}_k\right)$ 即可，

对于（2）式我们变形有

$\frac{1}{n}{d}_k^{-}<\frac{1}{n^2}D\left({\sum }_j^n{C}_{kj}\right)<\frac{1}{n}{d}_k^{+}$,

其中 $d_k^{-}是C_{kj}$ 里的最小波动值， $d_k^{+}$ 为相应最大波动值，那么我们只要证明

$\frac{1}{n}\left(d_1^{+}+d_2^{+}+...+d_m^{+}\right)<d_1+d_2+...+d_m(\ast )$ 即可，又由于 $d_k^{+}<\infty$ ,

那么（*）式显然成立的，可从极限角度思考， $n\to \infty$ 不等式左端远远小于右端，因为 $d_1^{+}+d_2^{+}+...+d_m^{+}<sup$，有上确界存在，而且当我们蒙特卡洛循环次数越多，我们的聚类数目整体产生波动会越，结果越来越平稳。

• 以上理论的正确性可以用个很普遍很好的例子形象说明
  

图7

图7就是我们模拟的原始波动（选取相应随机数即可，这里用的是标准正态分布随机数）与重复循环再取均值的效果图，很明显循环越多，最后波动越平稳。

五：总结与展望

本篇文章内容主要涉及的东西比较多，有理论上说明我们蒙特卡洛方法的有效性并陈述了一些聚类数目的方法，并通过相应实验来说明理论的有效性并解决实际问题。对于想学习这方面的朋友，如果帮助到一些，那是再好不过的事。