多种方法对建模数据做特征选择

前言

特征选择和特征提取都属于降维，就是试图去减少特征数据集中的属性(或者称为特征)的数目，但是两者所采用的方式方法却不同。特征提取的方法主要是通过属性间的关系，如组合不同的属性得到新的属性，这样就改变了原来的特征空间。特征选择的方法是从原始特征数据集中选择出子集，是一种包含的关系，没有更改原始的特征空间。特征提取和特征选择都是从原始特征中找出最有效（同类样本的不变性、不同样本的鉴别性、对噪声的鲁棒性）的特征。

一：基于统计方法选取特征

1：两两之间比较
对某个特征 $f$ ，假设数据集 $[x_1,x_2,...,x_n]$ 存在 $k$ 类$(k\le n)$，观察f在任意两类数据集之间是否显著不同

常见的方法：参数检验有 $t$ 检验， $z$ 检验等；非参数方法有$Wilcoxon$ 符号秩检验等等；还有就是观察 f 在两两不同类别组数据的平均值，用差异倍数来定夺是否表现不同。
2：总体一起选择
对某个特征 $f$ ，假设数据集 $[x_1,x_2,...,x_n]$ 存在$k$ 类$(k\le n)$，观察f在所有数据集之间是否显著不同

常见的方法：非参数检验之$Kruskal-Wallis$检验；还有一种方法是基于变异系数$（CV）$值，即求出每个类别中每个特征的变异系数，其中的最小值（或者均值）大于设定的阈值，可以把此特征视为此数据集的显著特征，当然$CV$法对于无监督数据也一样适用。

• 解释CV

当需要比较两组数据离散程度小的时候，如果两组数据的测量尺度相差太大，或者数据量纲的不同，直接使用标准差来进行比较不合适，此时就应当消除测量尺度和量纲的影响，而变异系数可以做到这一点，它是原始数据标准差与原始数据平均数的比。 $cv=\frac{\sigma }{u}$ 没有量纲，这样就可以进行客观比较了。

3：基于距离运算

这里我们之前的文章提到过，不再赘述！
基于距离运算筛选特征

4：基于卡方检验方法

卡方检验我们都知道其原理，首先建立二维列联表，然后求的统计量，再结合概率分布求得显著性p值。同样此方法也是可以进行特征显著性检验的，但是此方法也是要有标签数据的，否则是建立不出来二维列联表的。接下来我们将基于实际数据集进行相关实验。

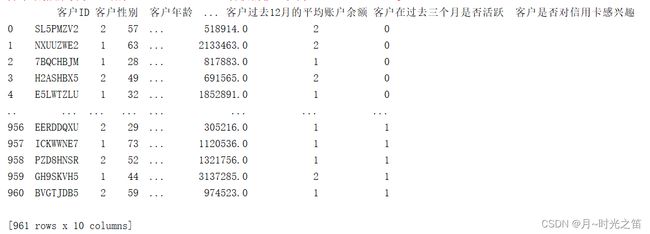
此次建模数据集大致如下图所示：

图1

####二联表卡方检验
def Chi_test(col):

    print('\033[1;34m{0:*^80}\033[0m'.format('卡方检验筛选变量'))
    p_ls = []
    for i in col:
        print('\033[1;34m{0:*^80}\033[1;0m'.format('自变量：%s'%i))
        datax = res3[i]
        datay = res3['客户是否对信用卡感兴趣']
        minx = datax.min()
        maxx = datax.max()
        LStemp1, LStemp2, LStemp3 = [], [], []
        if i == '客户性别' or i == '客户在过去三个月是否活跃' or  i == '客户是否有活跃的信贷产品':
            interval = [1, 2, 3]##因为此字段下的变量只有两个值，离散结果只有两种，所以要分开处理！！
            count = 0
            for l in range(len(interval) - 1):
                count = count + 1
                forwardvalue = interval[l]
                backvalue = interval[l + 1]
                lstemp1, lstemp2 = [], []
                for j, k in zip(list(datax), list(datay)):
                    if forwardvalue <= j < backvalue:
                        strmsg = str(round(forwardvalue, 2)) + '--' + str(round(backvalue, 2))
                        lstemp1.append(strmsg)
                        lstemp2.append(k)
                # print('\033[1;31m段%s基础信息：%s\033[0m' % (count, lstemp1))
                # print('\033[1;32m段%s违约信息：%s\033[0m' % (count, lstemp2))
                LStemp1.append(lstemp1[0])
                LStemp1.append(lstemp1[0])
                LStemp2.append(1)
                LStemp2.append(0)
                LStemp3.append(lstemp2.count(1))
                LStemp3.append(lstemp2.count(0))
        else:
            interval = np.linspace(minx, maxx, 5)
            count = 0
            LStemp1, LStemp2, LStemp3 = [], [], []
            for l in range(len(interval) - 1):
                count = count + 1
                forwardvalue = interval[l]
                backvalue = interval[l + 1]
                lstemp1, lstemp2 = [], []
                for j, k in zip(list(datax), list(datay)):
                    if forwardvalue <= j <= backvalue:
                        strmsg = str(round(forwardvalue, 2)) + '--' + str(round(backvalue, 2))
                        lstemp1.append(strmsg)
                        lstemp2.append(k)
                LStemp1.append(lstemp1[0])
                LStemp1.append(lstemp1[0])
                LStemp2.append(1)
                LStemp2.append(0)
                LStemp3.append(lstemp2.count(1))
                LStemp3.append(lstemp2.count(0))
        df = pd.DataFrame({'“%s”段值' % i: LStemp1, '否对信用卡感兴趣': LStemp2, '人数统计': LStemp3})
        print('\033[1;31m{0:*^40}\033[1;0m'.format('“%s”原始表' % i))
        print(df)
        cross_tab = pd.pivot_table(data=df, values='人数统计', index='“%s”段值' % i, columns='否对信用卡感兴趣', margins=True,
                                   aggfunc=np.sum)
        print('\033[1;32m{0:*^40}\033[1;0m'.format('“%s”二维列联表' % i))
        print(cross_tab)
        kf = chi2_contingency(cross_tab)
        print('\033[1;35m检验结果：\033[0m')
        print('chisq-statistic=%.2f, p-value=%.6f, df=%s expected_frep=%s' % kf)
        p_ls.append(kf[1])
    select_ls = []
    for i,j in zip(p_ls,col):
        if i <= 0.01:
            select_ls.append(j)
    print('\033[1;32m最终符合要求的变量名为：%s\033[0m'%select_ls)
    print('\033[1;38m本来共%s个变量，最终还剩%s个，最终保留率：%.3f%%'%(data.shape[1]-1,len(select_ls),100*len(select_ls)/(data.shape[1]-1)))
    return select_ls
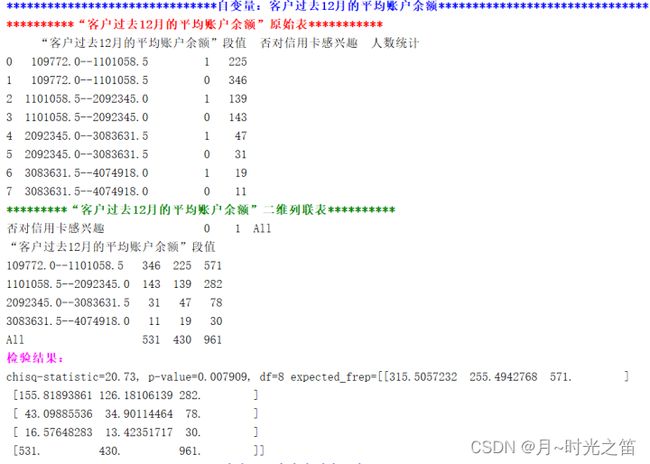
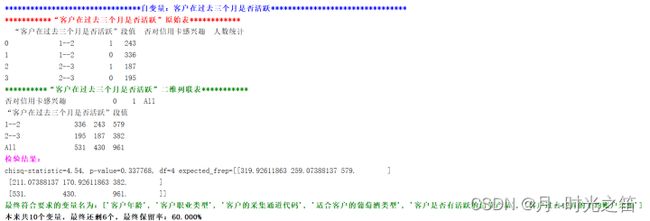
res = Chi_test(col_ls3)

图2

图3

上图2-3就是检验的过程（截取其中两个），所以这种非参数检验方法同样可以进行数据筛选，但前提是一定要建立正确的列联表，理解检验方法逻辑。

5：其他方法

比如简单的有特征之间相关性计算，相关性高的多个数据，可以取其中之一，对于监督和无监督学习数据都适用。还有就是一些新方法其他论文中提到的比如Relief-Based特征选择，XGBSFS算法等等。

二：基于机器学习方法选取特征

这里主要还是对于有监督学习数据而言。

1：随机森林

随机森林特征重要性的原理解释（注：这里直接跳过决策树-随机森林算法相关基础知识，比如剪枝、袋外等）。

思想：判断每个特征在随机森林中的每颗树上做了多大的贡献，然后取个平均值，最后比一比特征之间的贡献大小。其中关于贡献的计算方式可以是基尼指数或袋外数据错误率。

• 基尼指数

$k$ 代表第 $k$ 个类别，共 $K$ 个，$p_k$ 代表类别 $k$ 的样本权重，
基尼指数公式为： $Gini(p)={\sum }_{k=1}^K{p}_k(1-p_k)$ ，

那么对于特征 $X_j$ ，在节点 $m$ 的重要性，用节点 $m$ 分枝前后的基尼指数变化量表示：
$VI{M}_{jm}^{Gini}=GIm-GIl-GIr$ ，这里 $GIl$ 和 $GIr$ 分别表示分枝后两个新节点的 $Gini$ 指数。

如果特征 $X_j$ 在决策树 i 中出现的节点在节点集合 $M$ 中，那么$X_j$在第 $i$ 棵树的重要性为：
$VI{M}_{ji}^{Gini}={\sum }_{m\in M}VI{M}_{jm}^{Gini}$ ，

假设随机森林共 $n$ 棵树，那么 $VI{M}_j^{Gini}={\sum }_{i=1}^{n}VI{M}_{ji}^{Gini}$ ，最后，我们再做归一化处理：

$rVI{M}_j^{Gini}=VI{M}_j^{Gini}/{\sum }_{f=1}^{F}VI{M}_t^{Gini}$ ，

其中分母为所有特征（共 $F$ 个）的增益之和，分子为特征 $X_j$ 的基尼指数。

• 基于袋外数据OOB法

对于其中一棵树 $T_i$ ，用$OOB$样本可以得到误差 $e_1$ ，然后随机改变$OOB$中的第 $j$ 列，保持其他列不变，对第 $j$ 列进行随机的上下置换，得到误差 $e_2$ 。至此，可以用 $\left|e_1-e_2\right|$ 来刻画特征 $j$ 的重要性。其依据就是，如果一个特征很重要，那么其变动后会非常影响测试误差，如果测试误差没有怎么改变，则说明特征 $j$ 不重要。 而该方法中涉及到的对数据进行打乱的方法通常有两种：
1:是使用uniform或者gaussian抽取随机值替换原特征；
2:是通过permutation的方式将原来的所有 $N$ 个样本的第 i 个特征值重新打乱分布（相当于重新洗牌）。

2：Xgboost和Lasso

对于Xgboost模型的基础知识，我们知道Xgboost是一个优化的分布式梯度增强库，旨在实现高效，灵活和便携。它的很大特点一是在求解损失函数时候，使用了牛顿法，将损失函数泰勒展开到二阶，误差精度提高，当然带来的坏处就是计算变得更加复杂；二是损失函数中加入了正则化项，训练时的目标函数由两部分构成，第一部分为梯度提升算法损失，第二部分为正则化项；三是节点的分裂方式经过了优化；最后我认为则是处理缺失值做了不一样的逻辑替换。

那么基于树结构的Xgboost在进行属性特征重要性选择时，则根据结构分数的增益情况计算出来选择哪个特征作为分割点,而某个特征的重要性就是它在所有树中出现的次数之和。也就是说一个属性越多的被用来在模型中构建决策树，它的重要性就相对越高。

Lasso说白了就是简单线性回归的损失函数加入了L-范数，在特征过多的时候不容易产生过拟合现象。因为Lasso算法可以使特征的系数进行压缩并且可以使某些回归系数为0，即不选用该特征，因此可以进行特征选择，可以有效的解决各特征之间存在的多重共线性问题。

三：实验代码

关于统计方法的相关代码，请参考上一篇文章！

共同代码

from xgboost import XGBClassifier
import matplotlib.pylab as plt
from sklearn import ensemble
import seaborn as sns
import pandas as pd
import numpy as np
plt.rcParams['font.sans-serif']=['SimHei']##中文乱码问题！
plt.rcParams['axes.unicode_minus']=False#横坐标负号显示问题！
plt.figure(figsize=(15, 8))
data = pd.read_excel('redwine.xlsx',index_col=0)
winenames = np.array(list(data))

def makefigure(arr1,arr2,c='b'):
    plt.figure(figsize=(15, 8))
    sorted_idx = np.argsort(arr1)
    barpos = np.arange(sorted_idx.shape[0]) + 0.5
    plt.barh(barpos, arr2[sorted_idx], align='center', color=c)
    plt.yticks(barpos, winenames[sorted_idx], fontsize=18)
    plt.xlabel('CV value', fontsize=18)
    plt.tick_params(labelsize=20, rotation=10)
    plt.show()

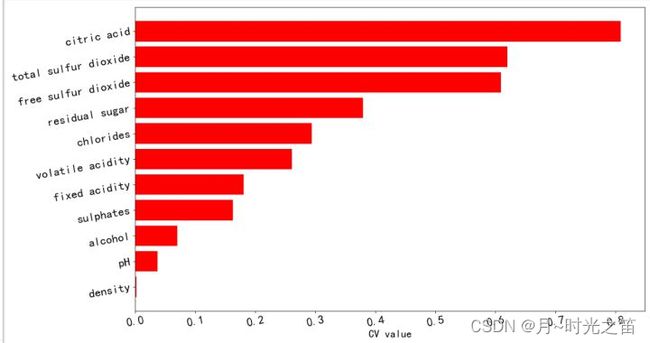
1：CV相关代码

quality_ls = list(set(data['quality']))
cols = list(data.iloc[:,:-1])
mean_ls = []
std_ls = []
nums = 2
for i in cols:
    m_ls = []
    s_ls = []
    for j in quality_ls:
        data_temp = data[data.quality==j][i]
        ls_sort = sorted(list(data_temp),reverse=True)
        ls_sort = ls_sort[nums:-nums]##去除前后极端值
        mean_res = np.array(ls_sort).mean() + 1e-8#防止分母为0
        std_res = np.array(ls_sort).std()
        m_ls.append(mean_res)
        s_ls.append(std_res)
    mean_ls.append(m_ls)
    std_ls.append(s_ls)
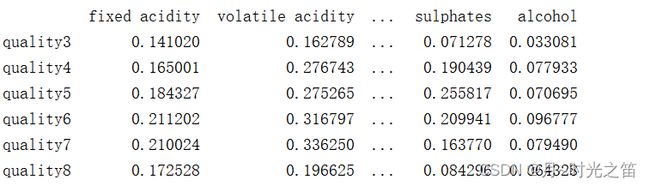
mean_df = pd.DataFrame(mean_ls,index=cols,columns=['quality' + str(i) for i in quality_ls]).T
std_df = pd.DataFrame(std_ls,index=cols,columns=['quality' + str(i) for i in quality_ls]).T
CV_df = std_df / mean_df
print(CV_df)
CV_df_mean = CV_df.mean()
CV_fin = np.array(list(CV_df_mean))
res1 = makefigure(CV_df_mean,CV_fin,'r')

图4：各类别CV值

图5：CV值展示

2：倍数计算相关代码

winename_ls = []
mul1 = 1.25
mul2 = 1.15
for i in cols:
    ls_means = []
    for j in quality_ls:
        data_temp = data[data.quality == j][i]
        mean_v = data_temp.mean()
        ls_means.append(mean_v)
    ###定义筛选逻辑
    meant_ls = sorted(ls_means,reverse=True)
    Max_v = max(ls_means)
    Min_v = min(ls_means)
    loc_Mn = quality_ls[ls_means.index(Max_v)]##最大值对应的数据标签位置
    Max_sec = meant_ls[1]##第二大值
    if Max_sec != 0:
        if Max_v / Max_sec >= mul1 and Max_v / Min_v >= mul2:
            D = dict(zip(quality_ls,ls_means))
            print('\033[1;32m符合要求的特征是：%s，在标签%s中，数值：%s，各类表现：%s\033[0m'%(i,loc_Mn,Max_v,D))
            winename_ls.append(i)
print('\033[1;34m最终满足上述要求的共%s个特征，分别是：%s\033[0m'%(len(set(winename_ls)),set(winename_ls)))

图6：倍数逻辑运行结果

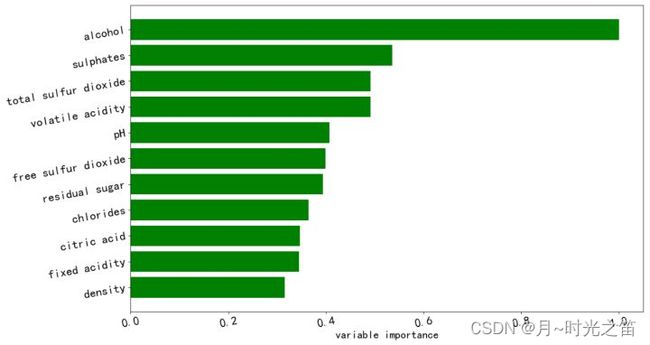
3：随机森林相关代码

x = data.iloc[:,:-1]
y = data.iloc[:,-1]
itrees = 180
depth = None
maxfeat = 11
#如果是回归，用RandomForestRegressor方法
winerfm = ensemble.RandomForestRegressor(n_estimators=itrees,max_depth=depth,max_features=maxfeat,oob_score=False,random_state=521)
####n_estimators:小会欠拟合，大会过拟合，大到一定层度提升不会太大，选个100左右；oob_score：是否采用袋外评估模型好坏
###min_samples_leaf：如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值
##决策树最大深度max_depth: 默认可以不输入，如果不输入的话，决策树在建立子树的时候不会限制子树的深度。一般来说，数据少或者特征少的时候可以不管这个值。如果模型样本量多，特征也多的情况下，推荐限制这个最大深度。常用的可以取值10-100之间。
##max_features有以下几种选取方法："auto", "sqrt", "log2", None。auto与sqrt都是取特征总数的开方，log2取特征总数的对数，None则是令max_features直接等于特征总数，而max_features的默认值是"auto"。
winerfm.fit(x,y)
featureimportance = winerfm.feature_importances_
featureimportance = featureimportance / featureimportance.max()
res2 = makefigure(featureimportance,featureimportance)

图7：随机森林

4：Xgboost和Lasso相关代码

plt.figure(figsize=(15, 8))
params={'max_depth':11,
        'n_estimators':100,
        'learning_rate':0.1,
        'nthread':4,
        'subsample':1.0,
        'colsample_bytree':0.5,
        'min_child_weight' : 3,
        'seed':361}
###XGBRegressor做回归预测
selectmodel = XGBClassifier(params)
bst = selectmodel.fit(x, y)
featureimportance = bst.feature_importances_
featureimportance = featureimportance / featureimportance.max()
sorted_idx = np.argsort(featureimportance)
sort_id = np.argsort(-featureimportance)
res3 = makefigure(featureimportance,featureimportance,'g')

####################
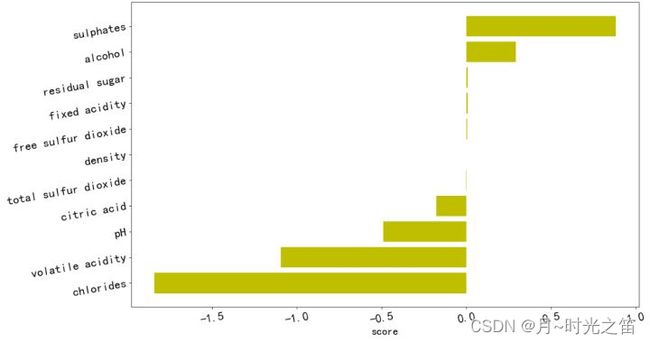
Lass_model = Lasso(alpha=0.0001,tol=1e-5)
Lass_model.fit(x,y) #用筛选后的特征数据来训练模型
co = Lass_model.coef_
res4 = makefigure(co,co,'y')

图8：Xgboost

图9：Lasso

注：以上学习模型基于回归方法同样能得到特征贡献值！

四：递归消除法

给定一个为特征分配权重的外部估计器（例如，线性模型的系数），递归特征消除（RFE）的目标是通过递归地考虑越来越小的特征集来选择特征。首先，估计器在初始特征集上进行训练，每个特征的重要性通过任何特定属性或可调用获得。然后，从当前的特征集中剪除最不重要的特征。该过程在修剪后的集合上递归重复，直到最终达到要选择的所需特征数量，这种方法原理性比较简单，简单有效但运算量大。

我们可以利用机器学习库：
from sklearn.ensemble import RandomForestClassifier as RFC
官方链接点击即可

五：总结

特征提取和特征筛选是有很大区别的，特征提取之后，原数据集可以说变得“面目全非”，特征筛选可以说是原数据集的一个子集，但两则的目的可以说是殊途同归的，都是为了降维，减少过拟合现象，减少运算复杂度。

但是每种检验方法我们务必要理解其底层含义，才能做到游刃有余，才能事半功倍，否则一味地堆积方法是不可取的，是很难解决实际问题的。