【1.线性分类器】线性分类器理论知识

一、图像分类任务

计算机视觉中的核心任务，目的是根据图像信息中所反映的不同特征，把不同类别的图像区分开来。

图像分类：从已知的类别标签集合中为给定的输入图片选定一个类别标签。

图像表示：像素表示（例如：RGB 表示）；全局特征表示（例如GIST：从图像上抽取一些频率的特征，适用于风景类，室内场景，大场景）；局部特征表示（例如 SIST 特征+词袋模型）

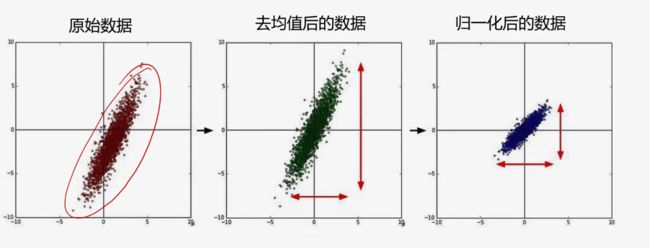
数据预处理：

分类器：近邻分类器、贝叶斯分类器、线性分类器、支持向量机分类器、神经网络分类器、随机森林、Adaboost

损失函数：0-1损失、多类支持向量机损失、交叉熵损失、L1损失、L2损失。损失函数输出通常是一个非负实值。

优化算法 (迭代优化)：一阶函数（梯度下降、随机梯度下降、小批量随机梯度下降）；二阶函数（牛顿法、BFGS、L-BFGS）

训练过程：数据集划分、数据预处理、数据增强、欠拟合与过拟合（减少算法复杂度、使用权重正则项、使用 droput 正则化）、超参数调整、模型集成

图像分类任务的评价指标：正确率（accuracy）=分对的样本数/ 全部样本数；错误率（error rate）=1-正确率；正确率分俩类：TOP1指标和TOP5指标
【模型评价指标】分析模型评价常用指标

---

二、线性分类器：

线性分类器是一种线性映射，将输入的图像特征映射为类别分数。

数据集：CIFAR-10 是一个用于识别普适物体的小型数据集。一共包含 10 个类别的 RGB 彩色图 片：飞机、汽车、鸟类、猫、鹿、狗、蛙类、马、船和卡车。图片的尺寸为 32×32 ，数据集中一共有 50000 张训练圄片和 10000 张测试图片。

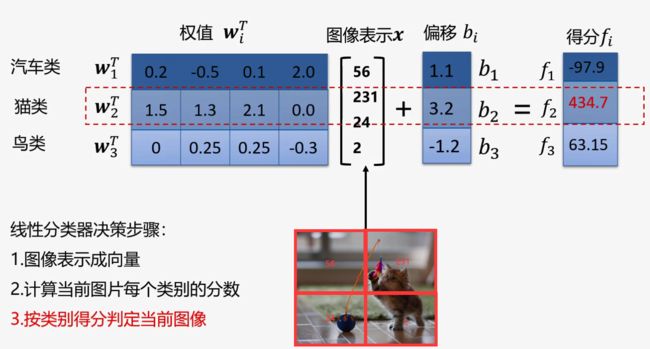
2.1 图像表示：

CIFAR-10中每一张图像转换为向量是32* 32 *3维列向量。x是图像向量，3072维；W是权值矩阵，维度10 *3072（权值看做一种模板，输入图像与评估模板的匹配程度越高，分类器输出分数越高）；b是偏置向量，维度10 *1维；f 为得分向量，维度10 *1维。

举例说明：

2.2 损失函数：

损失函数搭建了模型性能与模型参数之间的桥梁，指导模型参数优化。

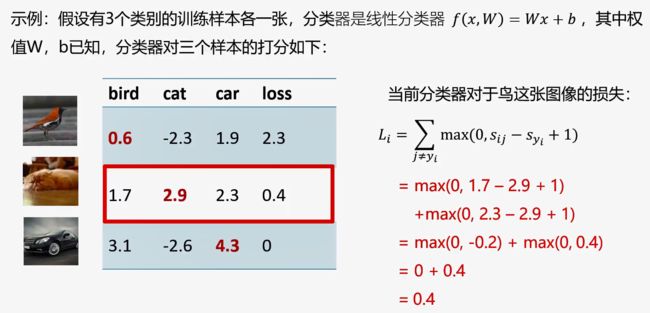
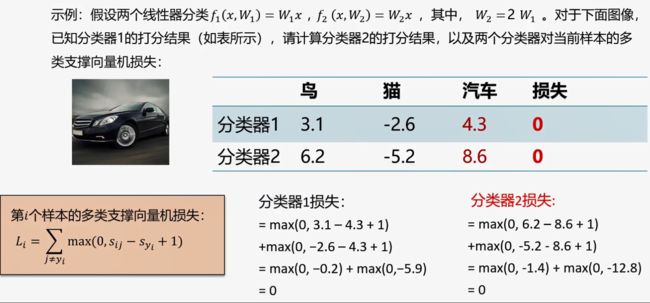
多类支持向量机损失：

max(0, .)损失常称为折页损失hingeloss

举例说明多类支持向量机损失Loss值的计算：

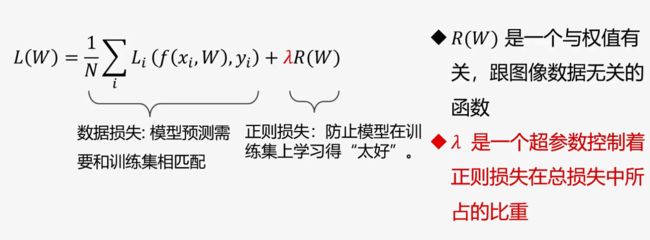
2.3 正则项与超参数：

出现的问题：存在不同的 W 使得损失函数L = 0，W 不唯一。

选择哪一个W ? 引入正则项：

正则项作用：1，使得唯一解；2，使得模型有偏好；3，使得模型不会过拟合

超参：是在开始学习前需设置值的参数，而不是学习得到。超参一般都会对模型性能有着重要的影响。超参使用验证集调整。

L2 正则损失对大数值权值进行惩罚，喜欢分散权值，鼓励分类器将所有维度特征用起来，而不是强烈依赖其中少数几维特征。

举例：

K折交叉验证：

如果数据很少，可能验证集包含样本就太少，从而无法统计上代表数据。

2.4 优化算法：

参数优化是机器学习的核心步骤之一，它利用损失函数的输出值作为反馈信号来调整分类器参数，以提升分类器对训练样本的预测性能。

损失函数L 是一个与参数W 有关的参数，优化的目标就是找到损失函数L 达到最优的那组参数W，说白了，就是求导数等于0时的W。（通常L 很复杂，很难直接求出W )

梯度下降法（SGD）：

往哪走：负梯度方向；走多远：步长来决定（学习率）

随机梯度下降：

每次随机选择一个样本 Xi 计算损失并更新梯度

小批量梯度下降法：

每次随机选择m（批量的大小）个样本，并计算损失并更新梯度（m一般取2的幂次作为批量大小，例如32或64或128个样本）

例：选m为100，即每选一次m就迭代 iteration为1次；batch-size是一次迭代所使用的样本量即为m；epoch：一个epoch表示所有样本被使用了一次