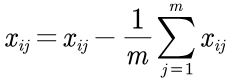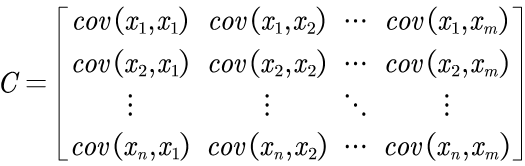主成分分析(PCA)及其可视化——matlab
本文所用为matlab2016a
matlab安装:待更新
matlab基础知识:待更新
如果本文内容已学会,可以看看python的哦
主成分分析(PCA)及其可视化——python_菜菜笨小孩的博客-CSDN博客
文章目录
一、主成分分析的原理
二、主成分分析的基本思想
三、主成分分析步骤
1.主成分分析的步骤:
2.部分说明
(1)球形检验(Bartlett)
(2)KMO(Kaiser-Meyer-Olkin)统计量
(3)主成分分析的逻辑框图
四、编程实现思路
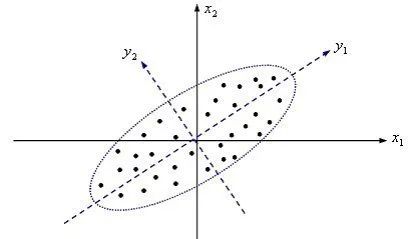
1.主成分向量投射图
2.算法步骤
1.数据标准化
2.数据为标准化
五、matlab主成分代码实现
1.读取数据
2.得到相关矩阵
(1)数据标准化做法
(2)数据未标准化做法
3.求相关矩阵的特征值和相对应的特征向量(在此以协方差阵为例)
4.画散点图和折线图
5.对特征值排序
6.求每个特征值的贡献度
7.累计贡献度
8.选出主成分,并得出相对应的矩阵
9.画色块矩阵图
完整代码:
总结及所遇到的问题解决办法:
一、主成分分析的原理
主成分分析是利用降维的思想,在损失很少信息的前提下把多个指标转化为几个综合指标的多元统计方法。通常把转化生成的综合指标称之为主成分,其中每个主成分都是原始变量的线性组合,且各个主成分之间互不相关,这就使得主成分比原始变量具有某些更优越的性能。这样在研究复杂问题时就可以只考虑少数几个主成分而不至于损失太多信息,从而更容易抓住主要矛盾,揭示事物内部变量之间的规律性,同时使问题得到简化,提高分析效率。
主成分分析正是研究如何通过原来变量的少数几个线性组合来解释原来变量绝大多数信息的一种多元统计方法。
二、主成分分析的基本思想
研究某一问题涉及的众多变量之间有一定的相关性,就必然存在着起支配作用的共同因素,并根据这一点,通过对原始变量相关矩阵或协方差矩阵内部结构关系的研究,利用原始变量的线性组合形成几个综合指标(主成分),在保留原始变量主要信息的前提下起到降维与简化问题的作用,使得在研究复杂问题时更容易抓住主要矛盾。
利用主成分分析得到的主成分与原始变量之间有如下基本关系:
1.每一个主成分都是各原始变量的线性组合
2.主成分的数目大大少于原始变量的数目
3.主成分保留了原始变量绝大多数信息
4.各主成分之间互不相关
三、主成分分析步骤
1.主成分分析的步骤:
1.根据研究问题选取初始分析变量;
2.根据初始变量特性判断由协方差阵求主成分还是由相关阵求主成分(数据标准化的话需要用系数相关矩阵,数据未标准化则用协方差阵);
3.求协差阵或相关阵的特征根与相应标准特征向量;
4.判断是否存在明显的多重共线性,若存在,则回到第一步;
5.主成分分析的适合性检验
6.得到主成分的表达式并确定主成分个数,选取主成分;
7.结合主成分对研究问题进行分析并深入研究。
2.部分说明
一组数据是否可以用主成分分析,必须做适合性检验。可以用球形检验和KMO统计量检验。
(1)球形检验(Bartlett)
球形检验的假设:
H0:相关系数矩阵为单位阵(即变量不相关)
H1:相关系数矩阵不是单位阵(即变量间有相关关系)
(2)KMO(Kaiser-Meyer-Olkin)统计量
KMO统计量比较样本相关系数与样本偏相关系数,它用于检验样本是否适于作主成分分析。
KMO的值在0,1之间,该值越大,则样本数据越适合作主成分分析和因子分析。一般要求该值大于0.5,方可作主成分分析或者相关分析。
Kaiser在1974年给出了经验原则:
0.9以上 适合性很好
0.8~0.9 适合性良好
0.7~0.8 适合性中等
0.6~0.7 适合性一般
0.5~0.6 适合性不好
0.5以下 不能接受的
(3)主成分分析的逻辑框图
![]()
四、编程实现思路
1.主成分向量投射图
2.算法步骤
1.数据标准化
1.标准化的数据均值为0,标准差为1;就是原数据减去均值,再除以标准差(无偏估计)
![]()
2.求相关系数矩阵
3、求协方差矩阵C的特征值和相对应的特征向量
![]()
u为C的特征向量,lamda为u的特征值
4、将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k列组成矩阵P
5、Y=PX即为降维到k维后的数据
2.数据为标准化
1、对所有指标进行中心化:去均值
2、求协方差矩阵C
其中μ为指标的均值
3、求协方差矩阵C的特征值和相对应的特征向量
![]()
u为C的特征向量,lamda为u的特征值
4、将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k列组成矩阵P
5、Y=PX即为降维到k维后的数据
五、matlab主成分代码实现
1.读取数据
此为读取csv数据,括号内1,0;表示从第一行第一列读取,matlab默认以0行,0列开始读取
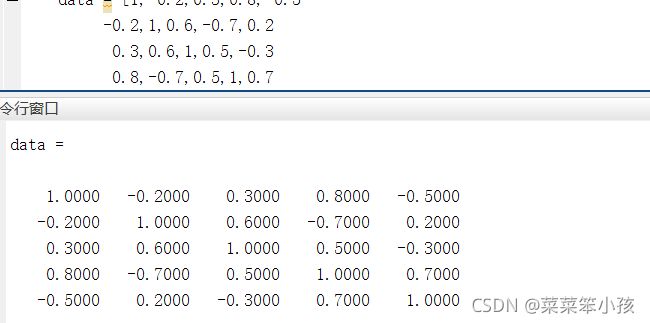
X= csvread('文件路径',1,0); %读取数据文件,第一行不读取在此举例一个数据 data 下面都是用此数据进行做:
data = [1,-0.2,0.3,0.8,-0.5
-0.2,1,0.6,-0.7,0.2
0.3,0.6,1,0.5,-0.3
0.8,-0.7,0.5,1,0.7
-0.5,0.2,-0.3,0.7,1]运行结果:
2.得到相关矩阵
(1)数据标准化做法
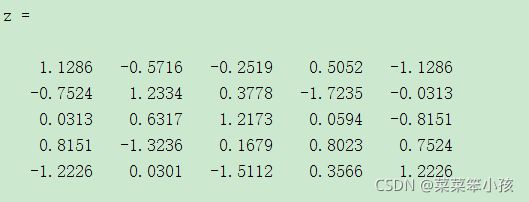
进行标准化:
z =zscore(data)运行结果:
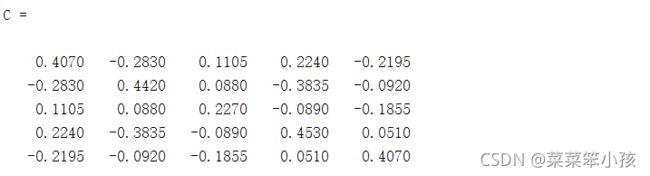
计算相关系数矩阵:
C = corr(z,'type','Pearson')运行结果:
(2)数据未标准化做法
计算均值:
mapping.mean = mean(data, 1) %计算均值进行中心化不会改变协方差阵的值,中心化不是标准化哦!!:
data = data - repmat(mapping.mean, [size(data, 1) 1])%去均值运行结果:
计算协方差阵:
C = cov(data) %协方差矩阵运行结果:
3.求相关矩阵的特征值和相对应的特征向量(在此以协方差阵为例)
[M, lambda] = eig(C) %求C矩阵特征向量及特征值运行结果:
取出协方差阵所求的对角线上的特征值,这只是其中一种做法,下面还有第二种
y = diag(lambda) %取出特征值矩阵中的特征值运行结果:
1时计算得到行数,2时计算得到列数,一个补充小知识点,嘻嘻嘻!!!
size(data,2) %读取数据文件中的列数运行结果:
4.画散点图和折线图
这里求得是x轴的值,上面取出的特征值即为y轴的值!!!
x = [size(data,2):-1:1] %表示变量个数并倒写出它们作为x轴 如 4,3,2,1
运行结果:
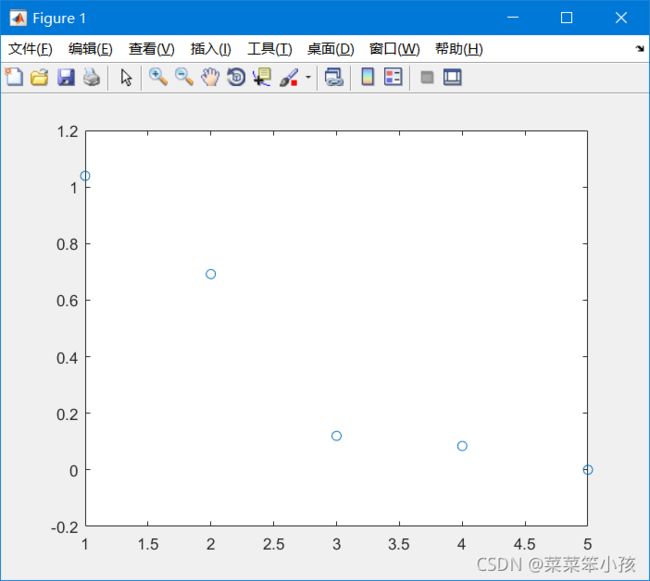
先画的散点图,x,y的值上面介绍了哦!!!
plot(x,y,'o') %绘制散点图运行结果:
显示上图中的格格线为 grid on ;关闭为 grid off
grid on; %显示格线运行结果:
因为我想在同一张图上画散点图和折线图,所以调用 hold on
hold on; %不换画布继续在这张画布上绘制给坐标轴取名 ,你随意,哈哈哈哈!!!
xlabel('x'); %x轴名称
ylabel('y'); %y轴名称运行结果:
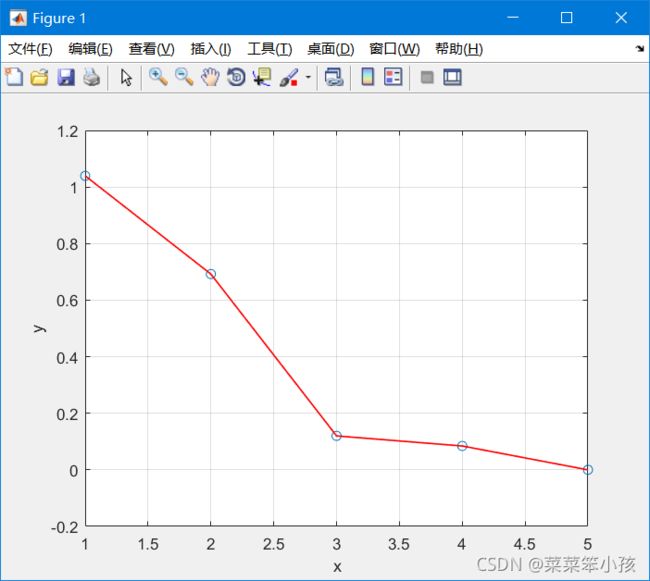
绘制折线图,颜色为红(’r‘) ,'lineWidth':线粗,这些基础知识,正在写,后续发布
plot(x,y,'-','Color','r','lineWidth',1) %绘制折线图运行结果:
5.对特征值排序
在此求出的 lambda 即为上方的 x,ind 即为 上方的 y;descend 为降序,默认升序
[lambda, ind] = sort(diag(lambda), 'descend') %排序运行结果:
6.求每个特征值的贡献度
即为每个特征值除以所有特征值的和,即占比
lambda=lambda./sum(lambda) %特征值的贡献度运行结果:
7.累计贡献度
计算累计贡献度
lambda=cumsum(lambda) %累计贡献度运行结果:
选出累计贡献度小于 85%之前的指标
为什么要选>85%呢?是为了方便后面的索引
k=find(lambda>0.85) %选出贡献率达到85的指标前K个运行结果:
让我们看一下k(1)等于多少???
k(1)运行结果:
那 1:k(1) 呢,又是多少???
1:k(1)运行结果:
但我们看上面累计贡献度时符合条件<85%的只有一个,所以我们下方选主成分应该有有变化
8.选出主成分,并得出相对应的矩阵
选出前K列的特征向量矩阵
M = M(:,ind(1:k(1)-1) %%取前k列
M = (-1)*M运行结果:
得到降维后的X
mappedX = data * M %降维后的X运行结果:
9.画色块矩阵图
通过此可以再次确定,下面画图需要设置的x,y的行数
mapping.M = M %映射的基运行结果:
设置色块矩阵图x,y轴所标注的名称
XVarNames={'A'}; %个数等于上面基的列数
YVarNames={'A','B','C','D','E'}; %个数等于上面基的行数数值矩阵图代码:
matrixplot(M,'FillStyle','nofill','XVarNames',XVarNames,'YVarNames',YVarNames)运行结果:
%色块颜色表示
matrixplot(M,'XVarNames',XVarNames,'YVarNames',YVarNames,'DisplayOpt','off','FigSize','Auto','ColorBar','on');
运行结果:
完整代码:
如不想每一步都有结果出现,请在每行代码最后加上英文版 ;
data = [1,-0.2,0.3,0.8,-0.5
-0.2,1,0.6,-0.7,0.2
0.3,0.6,1,0.5,-0.3
0.8,-0.7,0.5,1,0.7
-0.5,0.2,-0.3,0.7,1]
% z =zscore(data)
% C = corr(z,'type','Pearson')
mapping.mean = mean(data, 1) %计算均值
data = data - repmat(mapping.mean, [size(data, 1) 1])%去均值
C = cov(data) %协方差矩阵
[M, lambda] = eig(C) %求C矩阵特征向量及特征值
y = diag(lambda) %取出特征值矩阵中的特征值
size(data,2) %读取数据文件中的列数
x = [size(data,2):-1:1] %表示变量个数并倒写出它们作为x轴 如 4,3,2,1
plot(x,y,'o') %绘制散点图
grid on %显示格线
hold on; %不换画布继续在这张画布上绘制
xlabel('x'); %x轴名称
ylabel('y'); %y轴名称
plot(x,y,'-','Color','r','lineWidth',1); %绘制折线图
[lambda, ind] = sort(diag(lambda), 'descend') %排序
lambda=lambda./sum(lambda)
lambda=cumsum(lambda)
k=find(lambda>0.85) %选出贡献率达到95的指标前K个
M = M(:,ind(1:k(1)-1) %%取前k列
M = (-1)*M
mappedX = data * M %降维后的X
mapping.M = M %映射的基
XVarNames={'A'};
YVarNames={'A','B','C','D','E'};
matrixplot(M,'FillStyle','nofill','XVarNames',XVarNames,'YVarNames',YVarNames);
matrixplot(M,'XVarNames',XVarNames,'YVarNames',YVarNames,'DisplayOpt','off','FigSize','Auto','ColorBar','on');
总结及所遇到的问题解决办法:
因为我最近在学主成分,就整理了一些matlab和python的主成分代码,今天先发布matlab的,python的稍后发布(其实还没开始,最近要考期末了,很难受!!!)
在此学习中,遇到最头疼的的问题就行, matrixplot 无法应用,需要自己写入这个库才行,最终经过不懈努力解决了;还有在写色块矩阵图之前,我先写的热力图,研究半天没有学会,它那个显示的色块一点也不好看,于是才有了matrixplot,源码我先放文末,具体的解释,我也会稍后发布,非常感谢大家的支持,但如果我的文章有错误,请大家多多指出!!谢谢大家
matrixplot源码:
function matrixplot(data,varargin)
[0.7,0.7,0.7],'FigShap','s','FigSize','Auto','ColorBar','on');
% matrixplot(x,'TextColor','k','FigShap','d','FigSize','Full','ColorBar','on','FigStyle','Triu');
% XVarNames = {'xiezhh','heping','keda','tust','tianjin'};
% matrixplot(x,'FigShap','e','FigSize','Auto','ColorBar','on','XVarNames',XVarNames,'YVarNames',XVarNames);
% 对第一个输入参数类型进行判断
if ~ismatrix(data) || ~isreal(data)
error('输入参数类型不匹配:第一个输入参数应为实值矩阵');
end
% 解析成对出现的参数名/参数值
[FigShape,FigSize,FigStyle,FillStyle,DisplayOpt,TextColor,XVarNames,...
YVarNames,ColorBar,GridOpt] = parseInputs(varargin{:});
% 产生网格数据
[m,n] = size(data);
[x,y] = meshgrid(0:n,0:m);
data = data(:);
maxdata = nanmax(data);
mindata = nanmin(data);
rangedata = maxdata - mindata;
if isnan(rangedata)
warning('MATLAB:warning1','请检查您输入的矩阵是否合适!');
return;
end
z = zeros(size(x))+0.2;
sx = x(1:end-1,1:end-1)+0.5;
sy = y(1:end-1,1:end-1)+0.5;
if strncmpi(FigStyle,'Tril',4)
z(triu(ones(size(z)),2)>0) = NaN;
sx(triu(ones(size(sx)),1)>0) = NaN;
elseif strncmpi(FigStyle,'Triu',4)
z(tril(ones(size(z)),-2)>0) = NaN;
sx(tril(ones(size(sx)),-1)>0) = NaN;
end
sx = sx(:);
sy = sy(:);
id = isnan(sx) | isnan(data);
sx(id) = [];
sy(id) = [];
data(id) = [];
if isempty(XVarNames)
XVarNames = strcat('X',cellstr(num2str((1:n)')));
else
if (iscell(XVarNames) && (numel(XVarNames) ~= n)) || (~iscell(XVarNames) && (size(XVarNames,1) ~= n))
error('X轴方向变量名应为字符串矩阵或字符串元胞数组,其长度与输入矩阵的列数相同');
end
end
if isempty(YVarNames)
YVarNames = strcat('Y',cellstr(num2str((1:m)')));
else
if (iscell(YVarNames) && (numel(YVarNames) ~= m)) || (~iscell(YVarNames) && (size(YVarNames,1) ~= m))
error('Y轴方向变量名应为字符串矩阵或字符串元胞数组,其长度与输入矩阵的行数相同');
end
end
% 绘图
figure('color','w',...
'units','normalized',...
'pos',[0.289165,0.154948,0.409956,0.68099]);
axes('units','normalized','pos',[0.1,0.022,0.89,0.85]);
if strncmpi(GridOpt,'On',2)
mesh(x,y,z,...
'EdgeColor',[0.7,0.7,0.7],...
'FaceAlpha',0,...
'LineWidth',1); % 参考网格线
end
hold on;
axis equal;
axis([-0.1,n+0.1,-0.1,m+0.1,-0.5,0.5]);
view(2);
% 设置X轴和Y轴刻度位置及标签
set(gca,'Xtick',(1:n)-0.5,...
'XtickLabel',XVarNames,...
'Ytick',(1:m)-0.5,...
'YtickLabel',YVarNames,...
'XAxisLocation','top',...
'YDir','reverse',...
'Xcolor',[0.7,0.7,0.7],...
'Ycolor',[0.7,0.7,0.7],...
'TickLength',[0,0]);
axis off
% 绘制填充色块
if strncmpi(FillStyle,'Fill',3)
MyPatch(sx',sy',data',FigShape,FigSize);
end
% 显示数值文本信息
if strncmpi(DisplayOpt,'On',2)
str = num2str(data,'%4.2f');
scale = 0.1*max(n/m,1)/(max(m,n)^0.55);
if strncmpi(TextColor,'Auto',3)
ColorMat = get(gcf,'ColorMap');
nc = size(ColorMat,1);
cid = fix(mapminmax(data',0,1)*nc)+1;
cid(cid<1) = 1;
cid(cid>nc) = nc;
TextColor = ColorMat(cid,:);
for i = 1:numel(data)
text(sx(i),sy(i),0.1,str(i,:),...
'FontUnits','normalized',...
'FontSize',scale,...
'fontweight','bold',...
'HorizontalAlignment','center',...
'Color',TextColor(i,:));
end
else
text(sx,sy,0.1*ones(size(sx)),str,...
'FontUnits','normalized',...
'FontSize',scale,...
'fontweight','bold',...
'HorizontalAlignment','center',...
'Color',TextColor);
end
end
% 设置X轴和Y轴刻度标签的缩进方式
MyTickLabel(gca,FigStyle);
% 添加颜色条
if strncmpi(ColorBar,'On',2)
if any(strncmpi(FigStyle,{'Auto','Triu'},4))
colorbar('Location','EastOutside');
else
colorbar('Location','SouthOutside');
end
end
end
% ---------------------------------------------------
% 调整坐标轴刻度标签子函数
% ---------------------------------------------------
function MyTickLabel(ha,tag)
% 根据显示范围自动调整坐标轴刻度标签的函数
% ha 坐标系句柄值
% tag 调整坐标轴刻度标签的标识字符串,可用取值如下:
% 'Auto' --- 将x轴刻度标签旋转90度,y轴刻度标签不作调整
% 'Tril' --- 将x轴刻度标签旋转90度,并依次缩进,y轴刻度标签不作调整
% 'Triu' --- 将x轴刻度标签旋转90度,y轴刻度标签依次缩进
% Example:
% MyTickLabel(gca,'Tril');
if ~ishandle(ha)
warning('MATLAB:warning2','第一个输入参数应为坐标系句柄');
return;
end
if ~strcmpi(get(ha,'type'),'axes')
warning('MATLAB:warning3','第一个输入参数应为坐标系句柄');
return;
end
axes(ha);
xstr = get(ha,'XTickLabel');
xtick = get(ha,'XTick');
xl = xlim(ha);
ystr = get(ha,'YTickLabel');
ytick = get(ha,'YTick');
yl = ylim(ha);
set(ha,'XTickLabel',[],'YTickLabel',[]);
x = zeros(size(ytick)) + xl(1) - range(xl)/30;
y = zeros(size(xtick)) + yl(1) - range(yl)/70;
nx = numel(xtick);
ny = numel(ytick);
if strncmpi(tag,'Tril',4)
y = y + (1:nx) - 1;
elseif strncmpi(tag,'Triu',4)
x = x + (1:ny) - 1;
end
text(xtick,y,xstr,...
'rotation',90,...
'Interpreter','none',...
'color','r',...
'HorizontalAlignment','left');
text(x,ytick,ystr,...
'Interpreter','none',...
'color','r',...
'HorizontalAlignment','right');
end
% ---------------------------------------------------
% 根据散点数据绘制3维色块图子函数
% ---------------------------------------------------
function MyPatch(x,y,z,FigShape,FigSize)
% 根据散点数据绘制3维色块图
% MyPatch(x,y,z,FigShape,FigSize) x,y,z是实值数组,用来指定色块中心点三维
% 坐标。FigShape是字符串变量,用来指定色块形状。
% FigSize是字符串变量,用来指定色块大小。
%
% Example:
% x = rand(10,1);
% y = rand(10,1);
% z = rand(10,1);
% MyPatch(x,y,z,'s','Auto');
%
% 输入参数类型判断
if nargin < 3
error('至少需要三个输入参数');
end
if ~isreal(x) || ~isreal(y) || ~isreal(z)
error('前三个输入应为实值数组');
end
n = numel(z);
if numel(x) ~= n || numel(y) ~= n
error('坐标应等长');
end
if strncmpi(FigSize,'Auto',3) && ~strncmpi(FigShape,'Ellipse',1)
id = (z == 0);
x(id) = [];
y(id) = [];
z(id) = [];
end
if isempty(z)
return;
end
% 求色块顶点坐标
rab1 = ones(size(z));
maxz = max(abs(z));
if maxz == 0
maxz = 1;
end
rab2 = abs(z)/maxz;
if strncmpi(FigShape,'Square',1)
% 方形
if strncmpi(FigSize,'Full',3)
r = rab1;
else
r = sqrt(rab2);
end
SquareVertices(x,y,z,r);
elseif strncmpi(FigShape,'Circle',1)
% 圆形
if strncmpi(FigSize,'Full',3)
r = 0.5*rab1;
else
r = 0.5*sqrt(rab2);
end
CircleVertices(x,y,z,r);
elseif strncmpi(FigShape,'Ellipse',1)
% 椭圆形
a = 0.48 + rab2*(0.57-0.48);
b = (1-rab2).*a;
EllipseVertices(x,y,z,a,b);
elseif strncmpi(FigShape,'Hexagon',1)
% 六边形
if strncmpi(FigSize,'Full',3)
r = 0.5*rab1;
else
r = 0.5*sqrt(rab2);
end
HexagonVertices(x,y,z,r);
else
% 表盘形
if strncmpi(FigSize,'Full',3)
r = 0.45*rab1;
else
r = 0.45*sqrt(rab2);
end
DialVertices(x,y,z,r);
end
end
%--------------------------------------------------
% 求色块顶点坐标并绘制色块的子函数
%--------------------------------------------------
function SquareVertices(x,y,z,r)
% 方形
hx = r/2;
hy = hx;
Xp = [x-hx;x-hx;x+hx;x+hx;x-hx];
Yp = [y-hy;y+hy;y+hy;y-hy;y-hy];
Zp = repmat(z,[5,1]);
patch(Xp,Yp,Zp,'FaceColor','flat','EdgeColor','flat');
end
function CircleVertices(x,y,z,r)
% 圆形
t = linspace(0,2*pi,30)';
m = numel(t);
Xp = repmat(x,[m,1])+cos(t)*r;
Yp = repmat(y,[m,1])+sin(t)*r;
Zp = repmat(z,[m,1]);
patch(Xp,Yp,Zp,'FaceColor','flat','EdgeColor','flat');
end
function EllipseVertices(x,y,z,a,b)
% 椭圆形
t = linspace(0,2*pi,30)';
m = numel(t);
t0 = -sign(z)*pi/4;
t0 = repmat(t0,[m,1]);
x0 = cos(t)*a;
y0 = sin(t)*b;
Xp = repmat(x,[m,1]) + x0.*cos(t0) - y0.*sin(t0);
Yp = repmat(y,[m,1]) + x0.*sin(t0) + y0.*cos(t0);
Zp = repmat(z,[m,1]);
patch(Xp,Yp,Zp,'FaceColor','flat','EdgeColor','flat');
end
function HexagonVertices(x,y,z,r)
% 六边形
t = linspace(0,2*pi,7)';
m = numel(t);
Xp = repmat(x,[m,1])+cos(t)*r;
Yp = repmat(y,[m,1])+sin(t)*r;
Zp = repmat(z,[m,1]);
patch(Xp,Yp,Zp,'FaceColor','flat','EdgeColor','flat');
end
function DialVertices(x,y,z,r)
% 表盘形
% 绘制表盘扇形
maxz = max(abs(z));
t0 = z*2*pi/maxz-pi/2;
t0 = cell2mat(arrayfun(@(x)linspace(-pi/2,x,30)',t0,'UniformOutput',0));
m = size(t0,1);
r0 = repmat(r,[m,1]);
Xp = [x;repmat(x,[m,1]) + r0.*cos(t0);x];
Yp = [y;repmat(y,[m,1]) + r0.*sin(t0);y];
Zp = repmat(z,[m+2,1]);
patch(Xp,Yp,Zp,'FaceColor','flat','EdgeColor',[0,0,0]);
% 绘制表盘圆周
t = linspace(0,2*pi,30)';
m = numel(t);
Xp = repmat(x,[m,1])+cos(t)*r;
Yp = repmat(y,[m,1])+sin(t)*r;
Zp = repmat(z,[m,1]);
Xp = [Xp;flipud(Xp)];
Yp = [Yp;flipud(Yp)];
Zp = [Zp;flipud(Zp)];
patch(Xp,Yp,Zp,'FaceColor','flat','EdgeColor',[0,0,0]);
end
%--------------------------------------------------------------------------
% 解析输入参数子函数1
%--------------------------------------------------------------------------
function [FigShape,FigSize,FigStyle,FillStyle,DisplayOpt,TextColor,...
XVarNames,YVarNames,ColorBar,GridOpt] = parseInputs(varargin)
if mod(nargin,2)~=0
error('输入参数个数不对,应为成对出现');
end
pnames = {'FigShape','FigSize','FigStyle','FillStyle','DisplayOpt',...
'TextColor','XVarNames','YVarNames','ColorBar','Grid'};
dflts = {'Square','Full','Auto','Fill','On','k','','','Off','On'};
[FigShape,FigSize,FigStyle,FillStyle,DisplayOpt,TextColor,XVarNames,...
YVarNames,ColorBar,GridOpt] = parseArgs(pnames, dflts, varargin{:});
validateattributes(FigShape,{'char'},{'nonempty'},mfilename,'FigShape');
validateattributes(FigSize,{'char'},{'nonempty'},mfilename,'FigSize');
validateattributes(FigStyle,{'char'},{'nonempty'},mfilename,'FigStyle');
validateattributes(FillStyle,{'char'},{'nonempty'},mfilename,'FillStyle');
validateattributes(DisplayOpt,{'char'},{'nonempty'},mfilename,'DisplayOpt');
validateattributes(TextColor,{'char','numeric'},{'nonempty'},mfilename,'TextColor');
validateattributes(XVarNames,{'char','cell'},{},mfilename,'XVarNames');
validateattributes(YVarNames,{'char','cell'},{},mfilename,'YVarNames');
validateattributes(ColorBar,{'char'},{'nonempty'},mfilename,'ColorBar');
validateattributes(GridOpt,{'char'},{'nonempty'},mfilename,'Grid');
if ~any(strncmpi(FigShape,{'Square','Circle','Ellipse','Hexagon','Dial'},1))
error('形状参数只能为Square, Circle, Ellipse, Hexagon, Dial 之一');
end
if ~any(strncmpi(FigSize,{'Full','Auto'},3))
error('图形大小参数只能为Full, Auto 之一');
end
if ~any(strncmpi(FigStyle,{'Auto','Tril','Triu'},4))
error('图形样式参数只能为Auto, Tril, Triu 之一');
end
if ~any(strncmpi(FillStyle,{'Fill','NoFill'},3))
error('图形填充样式参数只能为Fill, NoFill 之一');
end
if ~any(strncmpi(DisplayOpt,{'On','Off'},2))
error('显示数值参数只能为On,Off 之一');
end
if ~any(strncmpi(ColorBar,{'On','Off'},2))
error('显示颜色条参数只能为On,Off 之一');
end
if ~any(strncmpi(GridOpt,{'On','Off'},2))
error('显示网格参数只能为On,Off 之一');
end
end
%--------------------------------------------------------------------------
% 解析输入参数子函数2
%--------------------------------------------------------------------------
function [varargout] = parseArgs(pnames,dflts,varargin)
% Copyright 2010-2011 The MathWorks, Inc.
% $Revision: 1.1.6.2 $ $Date: 2011/05/09 01:27:26 $
% Initialize some variables
nparams = length(pnames);
varargout = dflts;
setflag = false(1,nparams);
unrecog = {};
nargs = length(varargin);
dosetflag = nargout>nparams;
dounrecog = nargout>(nparams+1);
% Must have name/value pairs
if mod(nargs,2)~=0
m = message('stats:internal:parseArgs:WrongNumberArgs');
throwAsCaller(MException(m.Identifier, '%s', getString(m)));
end
% Process name/value pairs
for j=1:2:nargs
pname = varargin{j};
if ~ischar(pname)
m = message('stats:internal:parseArgs:IllegalParamName');
throwAsCaller(MException(m.Identifier, '%s', getString(m)));
end
mask = strncmpi(pname,pnames,length(pname)); % look for partial match
if ~any(mask)
if dounrecog
% if they've asked to get back unrecognized names/values, add this
% one to the list
unrecog((end+1):(end+2)) = {varargin{j} varargin{j+1}};
continue
else
% otherwise, it's an error
m = message('stats:internal:parseArgs:BadParamName',pname);
throwAsCaller(MException(m.Identifier, '%s', getString(m)));
end
elseif sum(mask)>1
mask = strcmpi(pname,pnames); % use exact match to resolve ambiguity
if sum(mask)~=1
m = message('stats:internal:parseArgs:AmbiguousParamName',pname);
throwAsCaller(MException(m.Identifier, '%s', getString(m)));
end
end
varargout{mask} = varargin{j+1};
setflag(mask) = true;
end
% Return extra stuff if requested
if dosetflag
varargout{nparams+1} = setflag;
if dounrecog
varargout{nparams+2} = unrecog;
end
end
end