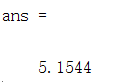3-1 二类LDA算法及MATLAB实现

3-1 二类LDA算法及MATLAB实现

1.二类LDA原理

\quad \quad LDA(Linear Discriminant Analysis)是是一种监督学习的降维技术。LDA的思想可以用一句话概括，就是“投影后类内方差最小，类间方差最大”，即分类依据是(协)方差。
注 在概率论和统计学中，协方差用于衡量两个变量的总体误差，设$x,y$是两个随机变量，则协方差定义为：
$cov(x,y)=E[(x-E(x))(y-E(y))]$

\quad \quad 对于二类LDA而言，它的输出结果是二维的。我们希望给定的数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近。
\quad \quad 假设数据集$D=(x_1,y_1),(x_2,y_2),\dots ,(x_m,y_m)$,其中任意样本$x_i$为$n$维向量,$y_i\in \{0,1\}$。我们定义$N_j,j=0,1$为第$j$类样本的个数(两数值一般相同)，$X_j$为第$j$类样本的集合，而$u_j(j=0,1)$为第$j$类样本的均值向量，定义${\sum }_j(j=0,1)$为第$j$类样本的协方差矩阵（严格说是缺少分母部分的协方差矩阵）.则：
\quad \quad \quad \quad $u_j=\frac{1}{N_j}\sum _{x\in X_j}x$
\quad \quad \quad \quad ${\sum }_j=\frac{1}{N_j}\sum _{x\in X_j}(x-u_j)(x-u_j{)}^T$
由于输出结果只有两类，我们将数据投影到一条直线上即可。

于是,分类的关键在于确定投影直线。不妨设投影直线是向量$w$,则对任意一个样本$x_i$,它在直线$w$的投影为$w^T{x}_i$,对于两个类别的中心点$u_0$, $u_1$,在直线$w$的投影为$w^T{u}_0$和$w^T{u}_1$。若要使得类间距离最大，即使得：
\quad \quad\quad \quad $||w^T{u}_0-w^T{u}_1|{|}_2^2$
最大化。若要使得同一种类别数据的投影点尽可能的接近，也就是要同类样本投影点的协方差：
\quad \quad\quad \quad $w^T{\sum }_{0}w$, \quad $w^T{\sum }_{1}w$
尽可能的小，即最小化
\quad \quad\quad \quad $w^T{\sum }_{0}w+w^T{\sum }_{0}w$。
于是，优化目标变为：
\quad $argmaxJ(w)=\frac{||w^T{u}_0-w^T{u}_1|{|}_2^2}{w^T{\sum }_{0}w+w^T{\sum }_{0}w}=\frac{w^T(u_0-u_1)(u_0-u_1{)}^{T}w}{w^T{\sum }_{0}w+w^T{\sum }_{0}w}$
为了计算优化目标，引入瑞利商的定义：
瑞利商是形如
\quad \quad\quad \quad $R(A,x)=\frac{x^{T}Ax}{x^{T}x}$
的函数，其中$x$是n维向量，$A$是$n\times n$的Hermitan矩阵，则瑞利商满足即它的最大值等于矩阵$A$最大的特征值，而最小值等于矩阵$A$的最小的特征值。

证：由正交变换的知识，$x^{T}Ax$可相似对角化为${\lambda }_1{y}_1^2+...+{\lambda }_n{y}_n^2$,则${\lambda }_{min}(y_1^2+...+y_n^2)\le {\lambda }_1{y}_1^2+...+{\lambda }_n{y}_n^2\le {\lambda }_{max}(y_1^2+...+y_n^2)$

回到本文，令类内散度矩阵$S_w$为
$S_w={\sum }_0+{\sum }_1=\sum _{x\in X_0}(x-x_0)(x-x_0{)}^T+\sum _{x\in X_1}(x-x_1)(x-x_1{)}^T$
同时定义类间散度矩阵$S_b$为
\quad \quad\quad \quad $S_b=(u_0-u_1)(u_0-u_1{)}^T$
则优化目标变为
\quad \quad\quad \quad $argmaxJ(x)=\frac{w^T{S}_{b}w}{w^T{S}_{w}w}$
显然，$S_w$正定，利用瑞利商的性质，$J(x)$的最大值为$S_w^{-\frac{1}{2}}{S}_b{S}_w^{-\frac{1}{2}}$的最大特征值。对应的$w$是$S_w^{-\frac{1}{2}}{S}_b{S}_w^{-\frac{1}{2}}$的最大特征值所对应的特征向量。

此时$S_w^{-1}{S}_b$的特征值与$S_w^{-\frac{1}{2}}{S}_b{S}_w^{-\frac{1}{2}}$的特征值相等，$S_w^{-1}{S}_b$的最大特征值所对应的特征向量$w^{\prime }=S_w^{-\frac{1}{2}}w$。
证明：设$A=S_w^{-\frac{1}{2}}{S}_b{S}_w^{-\frac{1}{2}}$，$B=S_w^{-1}{S}_b$,设$\lambda ,x$分别为$A$的特征值和特征向量，则
$Ax=S_w^{-\frac{1}{2}}{S}_b{S}_w^{-\frac{1}{2}}x=\lambda x$
等式两端同时左乘$S_w^{-\frac{1}{2}}$有：
$S_w^{-\frac{1}{2}}Ax=S_w^{-1}{S}_b{S}_w^{-\frac{1}{2}}x=S_w^{-\frac{1}{2}}\lambda x=\lambda S_w^{-\frac{1}{2}}x$
$⟺$
$B{S}_w^{-\frac{1}{2}}x=\lambda S_w^{-\frac{1}{2}}x$
从而$\lambda ,S_w^{-\frac{1}{2}}x$分别是$B$的特征值和特征向量。

2.算例与程序

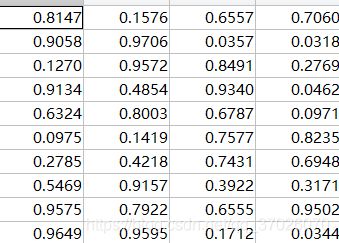
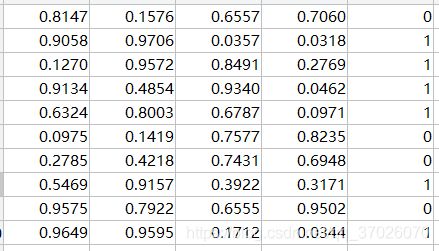
其他文章中讲的LDA算法实例也都不错，但由于不太好找例子，我只好用MATLAB及Excel造一个例子。
给定一个随机向量$A$,对随机生成的其他向量，若$Ax>c$(c为任意常数)，则类别分为1，反之分为0.显然分类依据是线形的。

令A=0，2，3，-4
B=
加上分类后的数据

编写程序求投影向量$w$

clc,clear
A=xlsread('test1.xlsx');
n=0;m=0;
[s,t]=size(A(:,1:end-1));
sum1=zeros(1,t);sum2=sum1;
for i=1:s
    if A(i,end)==1
        n=n+1;
        sum1=sum1+A(i,1:end-1);
    else
        m=m+1;
        sum2=sum2+A(i,1:end-1);
    end
end
u1=sum1./n;
u2=sum2./m;
u1=u1';u2=u2';
a1=zeros(t,t);a2=a1;
for i=1:s
    if A(i,end)==1
        a1=a1+(A(i,1:end-1)'-u1)*(A(i,1:end-1)'-u1)';
    else
        a2=a2+(A(i,1:end-1)'-u2)*(A(i,1:end-1)'-u2)';
    end
end
sw=a1+a2;
sb=(u1-u2)*(u1-u2)';
[x,y]=eig(sw\sb);
eigenvalue=diag(y);%求对角线向量
lamda=max(eigenvalue);%求最大特征值
for i=1:length(y)%求最大特征值对应的序数
    if lamda==eigenvalue(i)
        break;
    end
end
[m,n]=size(x);%得到行数和列数
y_lamda=x(:,i);%求矩阵最大特征值对应的特征向量
w=sw^(-1/2)*y_lamda;

验证：
随机生成一个向量$x1$

 x1=rand(10,1);

x=

用A作用x的判别结果（结果大于1判为1，否则为0）为（0）

用w作用x的判别结果

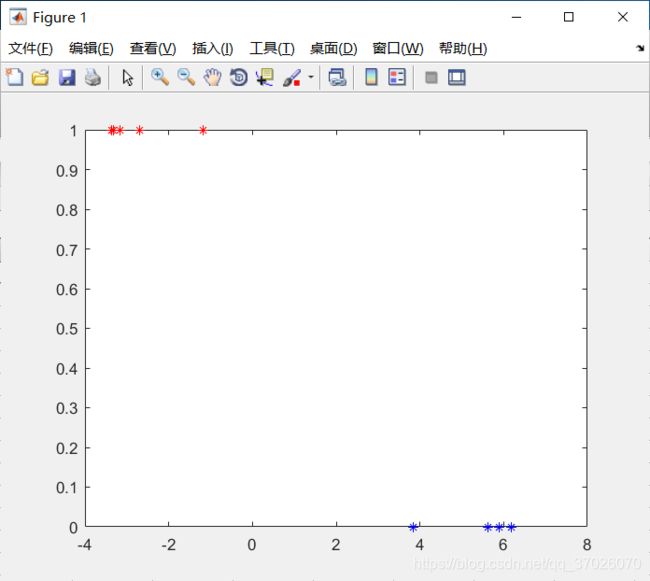
用w作用后为原矩阵(B)被将为1维

我们发现正值在原判别中是0，负值在原判别中是1，随机生成的x被w作用的值为正，判别结果应该为0，与被A作用结果相同。