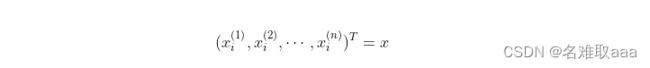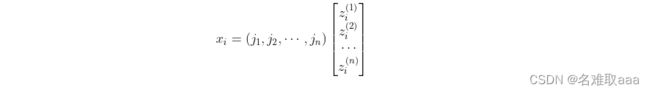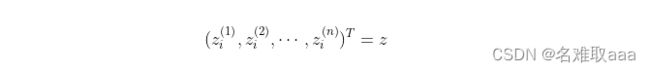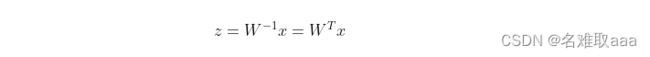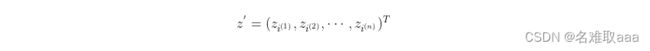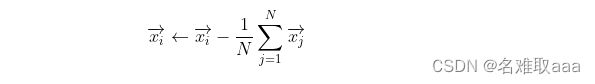机器学习數據降維之主成分分析(PCA)

---

前言

例如：随着人工智能的不断发展，机器学习这门技术也越来越重要，很多人都开启了学习机器学习，本文就介绍了机器学习的基础内容之主成分分析(PCA)

---

数据降维是什么？

数据降维又称维数约简，就是降低数据的维度。其方法有很多种，从不同角度入手可以有不同的分类，主要分类方法有：根据数据的特性可以划分为线性降维和非线性降维，根据是否考虑和利用数据的监督信息可以划分为无监督降维、有监督降维和半监督降维，根据保持数据的结构可以分为全局保持降维、局部保持降维和全局与局部保持一致降维等。需要根据特定的问题选择合适的数据降维方法。

数据降维一方面可以解决“维数灾难”，缓解信息丰富、知识贫乏的现状，降低复杂度，另一方面可以更好地认识和理解数据。

维度灾难与降维

维度灾难用来描述当空间维度增加时，分析和组织高维空间，因体积指数增加而遇到各种问题场景。例如在高维情况下，数据样本稀疏的问题。例如k近邻算法中，任意样本附近任意小的距离内总能找到一个训练样本，即训练样本的采样密度足够大才能保证分类性能，当特征维度很大时，满足密采样的样本数量会呈现指数级增大，大到几乎无法达到。所以在高维度情况下，涉及距离、内积的计算变得困难。

缓解维度灾难的一个重要途径就是降维。一般来说，想获得低维子空间，最简单的方法就是对原始高维度空间进行线性变换：给定d维空间中的样本X=(x1,x2,···,xm)变换之后得到的d’<=d维空间中的样本Z=W^TX。

变换矩阵W可视为d’个d维基向量，新空间中的属性是原空间属性的线性组合，基于线性变换来进行降维的方法都成线性维方法，主要区别于对低维子空间的性质有所不同，相当于对W施加了不同的约束。

作用

1. 减少模型分析的数据量，提升处理效率，降低计算难度
2. 实现数据可视化

主成分分析

主成分分析是一种最常用的无监督降维方法，通过降维技术吧多个变量化为少数几个主成分的统计分析方法。这些主成分能够反映原始变量的绝大部分信息，它们通常表示为原始变量的某种线性组合。

PCA原理

为了便于维度变换有如下假设：

• 假设样本数据是n维的。
• 假设原始坐标系为由标准正交基向量{i1,i2,···,in}张成的空间。
• 假设经过线性变换后的新坐标系为由标准正交基向量{j1,j2,···,jn}张成的空间。

根据定义有：

记ws=(js·i1,js·i2,···,js·in)，其各个分量就是基向量js在原始坐标系中的投影。

根据定义，有：

令坐标变换矩阵W为：W=(w1,w2,···,wn)，则有：

这样W的第s列就是js在原始坐标系中的投影。

假设样本点xi在原始坐标系中的表示为：

令其中：

假设样本点xi在新坐标系中的表示为：

令其中：

于是可以推导出：

丢弃其中的部分坐标，将维度降低到d

那么，现在出现一个问题，即丢弃哪些坐标？思想是：基于降低之后的坐标重构样本时，尽量要与原始样本接近。

PCA算法

算法的输入为样本集D与低维空间维数d，输出为所求的投影矩阵W。

算法的步骤表现在：

• 对所有样本进行中心化操作：
  
• 计算样本的协方差矩阵XX^T。
• 对协方差矩阵作特征值分解。
• 取最大的d个特征值对应的特征向量构造投影矩阵W。

通常低维空间维数的选取有两种方法：

• 通过交叉验证法选取较好的d。
• 从算法原理角度设置一个阈值，例如t=95%，然后选取使得下式成立的最小的d的值：

PCA降维有两个准则：

• 最近重构性：样本集中所有点，重构后的点距离原来点的误差之和最小。
• 最大可分性：样本点在低维空间的投影尽可能分开。

小例

目标:寻找k（k 核心：在信息损失尽可能少的情况下，降低数据维度

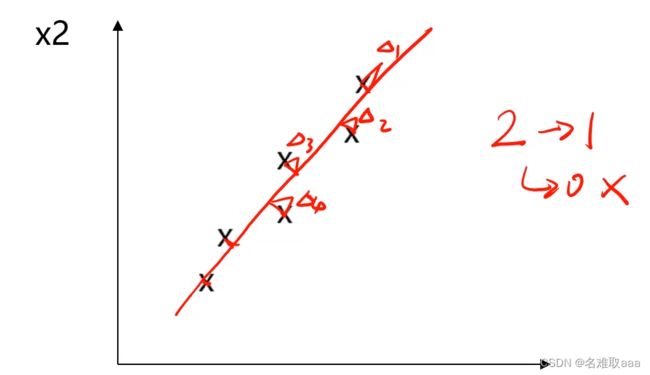
如圖，在我們把二維數據降為一維數據時，我們將其投影到一條直線上，這時為了使信息損失盡可能少，那麽數據投影到直線的距離就應該盡可能小。如果要把2維數據將為0維，那麽數據就丟失掉了，主要特征就沒了，這不是我們想看到的。

類似地，要把三維數據降為二維數據，就需要把三維數據投影到一個平面，然後為了使損失的數據盡可能少，就希望三維數據的各點到這個平面的距離盡可能小。
我們可以把這個投影的線或面理解成主成分，而各點到它們的距離可以理解成損失的信息。

說了這麽多，那麽如何保留主要信息呢？那就是投影後不同的數據要盡可能分得開(即不相關) 這是因為維度很高的數據是有很多的相關性的，而我們希望數據盡可能少，那我們就要保證每個維度裏的數據在不同的維度之間沒有太多的關系，也就可以理解成上述所說的投影後不同的數據要盡可能分得開(即不相關) 。

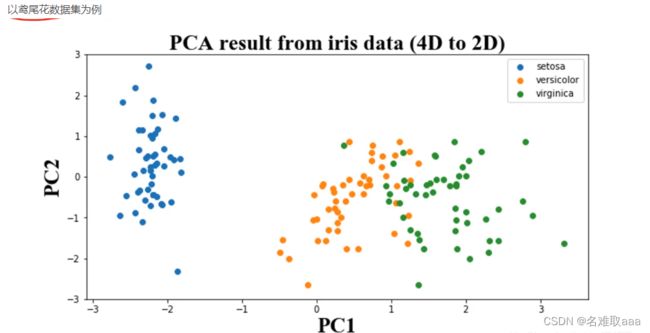
通過PCA方法將4維數據降為2維數據後，我們將其可視化，這時藍色代表一類花、橙色代表一類花、綠色代表一類花，這三個不同特征之間是分得比較開的，當已經找不到一個二維平面可以把數據分得比上圖更開，這時信息就是損失得最少的。

假設我們有n維數據，每個維度的量方是不一樣的，所以第一步我們要進行一個數據預處理。第二步我們得到方差後，可以根據這個方差來判斷相關性的大小，方差越大，它的相關性就越小，方差越小，它的相關性就越大。所以，假設我們有n維數據，如果它的k個維度的方差是比較大的，那麽我們就可以保留下來，另外n-k個維度的方差是比較小的，那麽就可以將其舍棄。

實戰

PCA實戰task：

1. 基於iris_data.csv數據，建立KNN模型實現數據分類(n_neighbors=3)
2. 對數據進行標準化處理，選取一個維度可視化處理后的效果
3. 進行與元數據等維度PCA，查看各主成分的方差比例
4. 保留合適的主成分，可視化降維后的數據
5. 基於降維后數據建立KNN模型，與原數據表型進行對比

#load data
import pandas as pd
import numpy as np
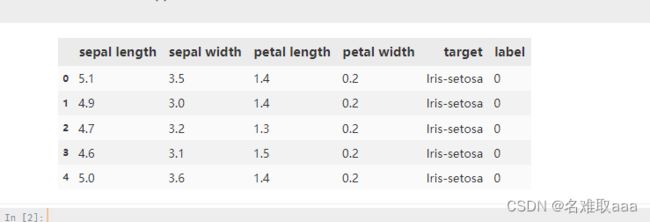
data = pd.read_csv('iris_data.csv')
data.head()

#define X and y
X = data.drop(['target','label'],axis=1)
y = data.loc[:,'label']
X.head()

#establish knn model and calculate the accuracy
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X,y)
y_predict = KNN.predict(X)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)

看一下accuracy_score，越接近1越好

from sklearn.preprocessing import StandardScaler
X_norm = StandardScaler().fit_transform(X)
print(X_norm)

#calcualte the mean and sigma
x1_mean = X.loc[:,'sepal length'].mean()
x1_norm_mean = X_norm[:,0].mean()
x1_sigma = X.loc[:,'sepal length'].std()
x1_norm_sigma = X_norm[:,0].std()
print(x1_mean,x1_sigma,x1_norm_mean,x1_norm_sigma)

from matplotlib import pyplot as plt
fig1 = plt.figure(figsize=(20,5))
plt.subplot(121)
plt.hist(X.loc[:,'sepal length'],bins=100)
plt.subplot(122)
plt.hist(X_norm[:,0],bins=100)
plt.show()

可視化看一下

#pca analysis
from sklearn.decomposition import PCA
pca = PCA(n_components=4)
X_pca = pca.fit_transform(X_norm)
#calculate the variance ratio of each principle components
var_ratio = pca.explained_variance_ratio_
print(var_ratio)

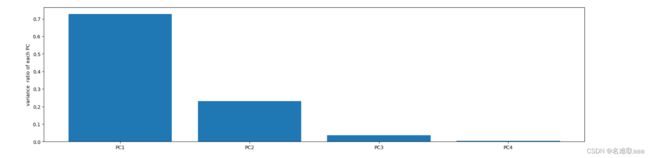
可以看出前兩個占的比例比較大，後面兩個不怎麽相關其實可以忽略

fig2 = plt.figure(figsize=(20,5))
plt.bar([1,2,3,4],var_ratio)
plt.xticks([1,2,3,4],['PC1','PC2','PC3','PC4'])
plt.ylabel('variance  ratio of each PC')
plt.show()

可視化看一下，也是看出後面兩個影響不大

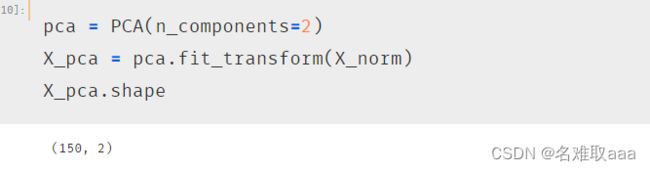
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_norm)
X_pca.shape

PCA降爲兩維度

#visualize the PCA result
fig3 = plt.figure(figsize=(10,10))
setosa=plt.scatter(X_pca[:,0][y==0],X_pca[:,1][y==0])
versicolor=plt.scatter(X_pca[:,0][y==1],X_pca[:,1][y==1])
virginica=plt.scatter(X_pca[:,0][y==2],X_pca[:,1][y==2])
plt.legend((setosa,versicolor,virginica),('setosa','versicolor','virginica'))
plt.show()

可視化PCA結果

KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X_pca,y)
y_predict = KNN.predict(X_pca)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)

再KNN訓練一下，accuracy_score可以看出非常接近1已經算不錯了

總結

PCA實戰summary：

• 通過計算數據對應主成分(principle components)，可在減少數據維度同時盡可能保留主要信息
• 為確定合適的主成分維度，可先對數據進行與原數據相同維度的PCA處理，再根據哥哥成分的數據方差確認主成分維度

這就是本次學習主要成分分析(PCA)的筆記
附上本次實戰的數據集和源碼：
鏈接：https://github.com/fbozhang/python/tree/master/jupyter