笔记——第十四届蓝桥杯模拟赛第一期第五题解法

问题描述

小蓝有一个 100 行 100 列的矩阵，矩阵的左上角为 1。其它每个位置正好比其左边的数大 2，比其上边的数大 1 。
例如，第 1 行第 2 列为 3，第 2 行第 2 列 为 4，第 10 行第 20 列为 48。
小蓝想在矩阵中找到一个由连续的若干行、连续的若干列组成的子矩阵，使得其和为 2022，请问这个子矩阵中至少包含多少个元素（即子矩阵的行数和列数的乘积）。

题目来源——网上

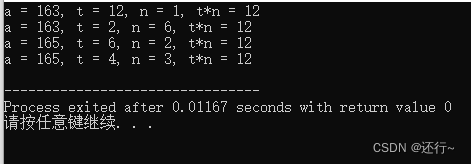
看到了很多暴力破解的方法，觉得这道题考察的是等差数列的算法。

首先有3个变量。
初值——a
列值——n
行值——t
（有变量名强迫症的，可以自行改一下。）

之后研究下题目可得：
a的最大值只能为
a_max = 100 x ( 100 - 1 ) x 2 = 298。
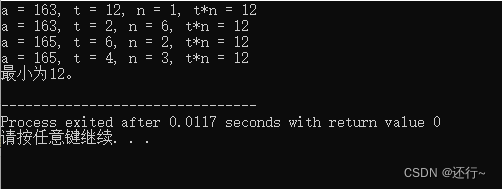
最小为1。
于是就可以限定a的范围。
同时行值和列值最大都是100，最小都是1。

由等差求和公式可知：

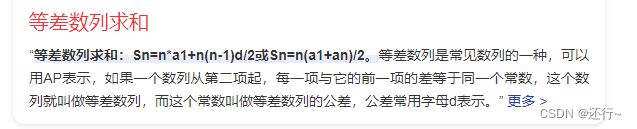
先算行的数列和值。
可得： (a + n - 1) x n。
之后通过观察，下一行的总和只会比上一行的多行数和。
于是将 第一行的总和设为 c
可得之后下面每一行的值为： c + （t - 1）x n。
于是全部和的总和为：

( t x ( (2 x c) + ((t - 1) x n) ) ) ÷ 2

转为C代码如下：

#include
int main()
{
	int c = 0;
	for(int a = 1;a <=298; a++)
	{
		for(int n = 1;n <= 100; n++)
		{
			for(int t = 1;t <= 100; t++)
			{
				c = (a + n - 1) * n;
				if( (t * ( (2 * c) + ((t - 1) * n) ))  == 4044)
				{
					printf("a = %d, t = %d, n = %d, t*n = %d\n",a,t,n,n*t);
				}
			}
		}
	}
	return 0;
}

运行图

答案就摆上上面。
按照题意的话，可以这样修改。

#include
int main()
{
	int c = 0,min = 2022;
	for(int a = 1;a <=298; a++)
	{
		for(int n = 1;n <= 100; n++)
		{
			for(int t = 1;t <= 100; t++)
			{
				c = (a + n - 1) * n;
				if( (t * ( (2 * c) + ((t - 1) * n) ))  == 4044)
				{
					printf("a = %d, t = %d, n = %d, t*n = %d\n",a,t,n,n*t);
					if(min > t*n)min = t*n;
				}
			}
		}
	}
	printf("最小为%d。\n",min);
	return 0;
}

运行图

易错点：

1、a的最大值，一开始设为了100。
2、数列的计算。

修改

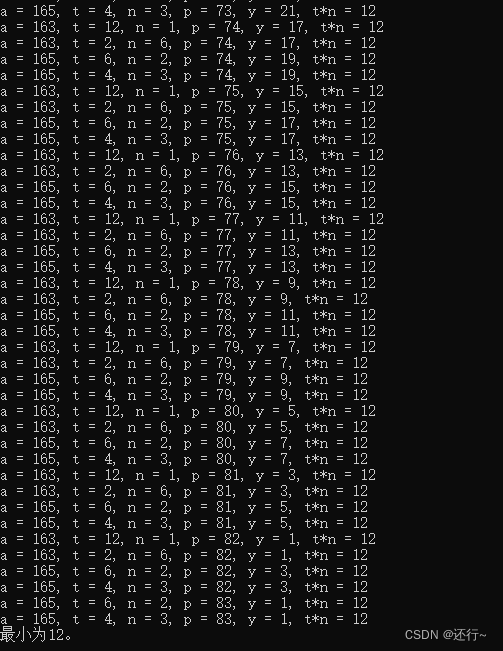
由于可能会出现边界问题，于是我对代码进行了修改。

首先找a在某一个位置的值，可以由题目可得，横向每次加2，纵向每次加一，起始位置为1.
不难得出：
a = （p - 1）x 2 + y
p为横向坐标，坐标从零开始。
y为纵向坐标，坐标从零开始。
之后只要让p + n和y + t 都不要大于100就行了。
于是按照这个修改代码可得：

#include
int main()
{
	int c = 0,min = 2022;
	int a;
	for(int p = 1;p <=100; p++)
	{
		for(int y = 1;y <=100; y++)
		{
			a = 2 * (p - 1) + y;
			for(int n = 1;n <= 100-p; n++)
			{
				for(int t = 1;t <= 100-y; t++)
				{
					c = (a + n - 1) * n;
					if( (t * ( (2 * c) + ((t - 1) * n) ))  == 4044)
					{
						printf("a = %d, t = %d, n = %d, p = %d, y = %d, t*n = %d\n",a,t,n,p,y,n*t);
						if(min > t*n)min = t*n;
					}
				}
			}
		}
	}
	printf("最小为%d。\n",min);
	return 0;
}

运行图