深度学习【5】卷积神经网络CNN（2）
文章目录
- 一.卷积的变种
-
- 1.分组卷积
-
- (1).定义
- (2).优势
- (3).应用场景
- 2.转置卷积
-
- (1).定义
- (2).优势
- (3).具体步骤
- (4).应用场景
- 3.空洞卷积
-
- (1).定义
- (2).优势
- (3).应用场景
- 4.可变形卷积
-
- (1).定义
- (2).优势
- (3).实现过程
- 二.1x1卷积的作用
-
- 1.实现信息的跨通道交互和整合
- 2.对卷积核通道数进行降维和升维，减小参数量
- 三.卷积核的大小
- 四.每层卷积的卷积核尺寸种类
- 五.如何减少卷积层参数量
一.卷积的变种
随着卷积神经网络在各种问题中的广泛应用，卷积层也逐渐衍生出许多变种。除了之前提到的标准卷积，最常见到的有空洞卷积（Dilated Convolution），转置卷积（Transposed Convolution），分组卷积（Group Convolution）和可变形卷积（Deformable Convolution）。
1.分组卷积
在普通的卷积操作中，一个卷积核对应输出通道的一个通道，而每个卷积核又会作用在输入特征图的所有通道上，因此输出特征图的每个通道都和输入特征图的所有通道相连接，即在普通的卷积操作中，每个输出通道与输入通道是“全连接”的状态。
(1).定义
下图为普通卷积的示意图：
输入特征图的通道数为 c 1 c_1 c1，卷积核的个数为 c 2 c_2 c2，输出特征图的通道数为 c 2 c_2 c2，每个卷积核都要与输入特征图的每个通道进行卷积计算。
下图为分组卷积的示意图：
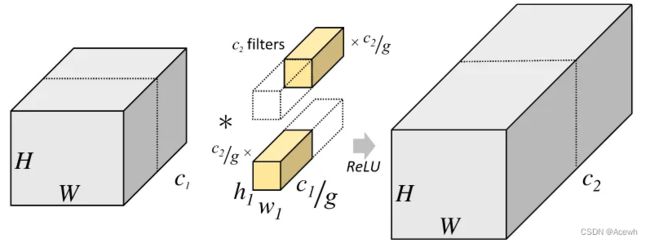
g g g 表示分组卷积的组数（图中为2个组，原先的 c 2 c_2 c2 个卷积核分为两组），输入特征图也对应的分为 g g g 组，每组卷积核与对应的输入特征图组进行卷积运算，最后会生成 g g g 组输入特征图，它们合并后输出特征图最终也是 c 2 c_2 c2 个通道。
(2).优势
- 如果分组卷积的组数为 g g g，它能够将卷及操作的参数里和计算量都降为普通卷积的 1 / g 1/g 1/g，不容易过拟合。
- 某些情况下，分组卷积的模型效果要由于普通卷积，因为分组卷积的方式能够增加相邻层卷积核之间的对角相关性。
(3).应用场景
分组卷积最初是在AlexNet网络中引入的，当时为了解决单个GPU无法处理含有较大计算量和存储需求的卷积层问题，就采用分组卷积将计算和存储分配到多个GPU上，后来随着硬件的不断升级，这个方向上的需求已经大为减少。目前，分组卷积更多地被用来构建用于移动设备的小型网络模型。
2.转置卷积
(1).定义
转置卷积不是卷积的逆运算，它是先对输入特征进行填充，使其维度扩大到适配卷积目标输出维度，然后将卷积核参数翻转，进行普通的卷积操作的一个过程，其输入到输出的维度变换关系恰好与普通卷积的变换关系相反，这个变换并不是真正的逆变换操作，通常称为转置卷积，而不是反卷积（Deconvolution）。
(2).优势
转置卷积最大的作用就是上采用（UpSampling）。
(3).具体步骤
具体操作步骤如下：
- 在输入特征图元素间填充 s − 1 s-1 s−1 行列的0元素；
- 在输入特征图四周填充 k − p − 1 k-p-1 k−p−1 行列的0元素；
- 将卷积核参数上下、左右翻转；
- 做正常卷积操作（填充0，步长为1）。
设普通卷积时的步长为 s s s，卷积核大小为 k k k，填充表示 p p p。输入的特征如图为2x2：
卷积核为3x3：
| 步骤 | s=1,p=0,k=3 | s=2,p=0,k=3 | s=2,p=1,k=3 |
|---|---|---|---|
| 1 | s − 1 = 1 − 1 = 0 s-1=1-1=0 s−1=1−1=0 |
s − 1 = 2 − 1 = 1 s-1=2-1=1 s−1=2−1=1 |
s − 1 = 2 − 1 = 1 s-1=2-1=1 s−1=2−1=1 |
| 2 | k − p − 1 = 3 − 0 − 1 = 2 k-p-1=3-0-1=2 k−p−1=3−0−1=2 |
k − p − 1 = 3 − 0 − 1 = 2 k-p-1=3-0-1=2 k−p−1=3−0−1=2 |
k − p − 1 = 3 − 1 − 1 = 1 k-p-1=3-1-1=1 k−p−1=3−1−1=1 |
| 3 |  |
|
|
| 4 |  |
 |
 |
转置卷积后的输出特征图大小为： n e w = ( o l d − 1 ) ∗ s − 2 ∗ p + k new = (old-1)*s-2*p+k new=(old−1)∗s−2∗p+k。
注意： o l d , s p k old,spk old,spk 是做转置卷积之前普通卷积的参数，并不是转置卷积过程中变化后的参数。
(4).应用场景
- 语义分割、实例分割等任务：提取输入图像的高层语义信息，网络的特征图一般会缩小聚合，而网络的输出又需要与源图像大小一致的分割结果，这时候就用到了转置卷积。
- 物体检测、关键点检测：需要输出与源图像大小一致的热图。
- 图像的自编码器、变分自编码器、生成对抗网络等。
3.空洞卷积
在某些任务中需要将小尺寸特征图还原到源图像的大小，比如常见的语义分割模型FCN，一般采用池化操作来扩大特征图的感受野，但是会降低特征图的分辨率，丢失一些特征信息，导致后续的转置卷积无法还原一些细节，从而限制最终分割精度的提升。
(1).定义
空洞卷积，又名扩张卷积、带孔卷积，就是在标准卷积核中注入“空洞”，以增加卷积核的感受野。空洞卷积引入了扩张率（Dilation Rate） 这个超参数来指定相邻采样点之间的间隔：比如扩张率为r的空洞卷积，卷积核上相邻数据点之间有 r − 1 r-1 r−1 个空洞。尺寸为 KxK 标准卷积核，其对应的扩张率为r的空洞卷积核尺寸为 K + ( r − 1 ) ( K − 1 ) K+(r-1)(K-1) K+(r−1)(K−1)。
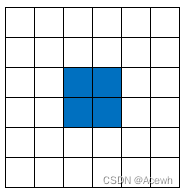
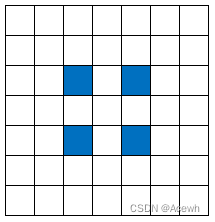
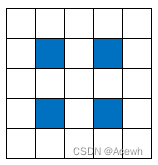
假设标准卷积核的尺寸为3x3，下图为3种扩张率的空洞卷积，绿点为空洞卷积的边界，是有效的采样点，而黄色为空洞。
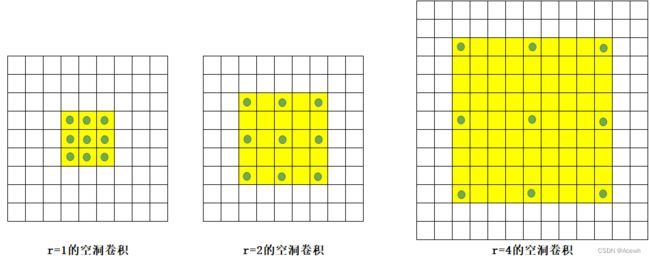
(2).优势
- 扩大卷积核尺寸，不经过下采样就可增大感受野。
- 保留输入数据的内部结构。
(3).应用场景
实时图像分割领域。
4.可变形卷积
(1).定义
普通的卷积操作实在固定的、规则的网格点上进行数据采样，如下图（a），这束缚了网络的感受野形状，限制了网络对几何形变的适应能力。为了克服这个限制，可变形卷积在卷积核的每个采样点参数上添加了一个可学习的偏移量（offset），让采样点不再局限于规则的网格点，如下图（b）。而下图（c）在水平上对卷积核有较大拉伸，有点类似于空洞卷积。下图（d）是对卷积核进行旋转，是可变形卷积的特例。
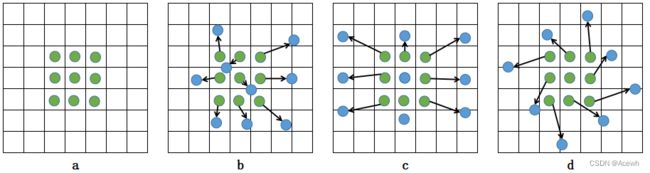
(2).优势
可变形卷积让网络具有了学习空间几何形变的能力，具体来说就是可变形卷积引入了一个平行分支来端到端地学习卷积核采样点的位置偏移量，这种结构让可变形卷积的采样点能根据当前图像的内容进行自适应调整。
(3).实现过程
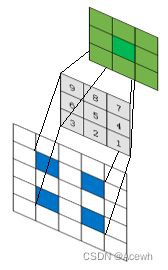
如下图所示：
- 我们在得到一个输入特征图后，对其施加一个卷积层；
- 然后得到一个偏移量；
- 偏移量的通道维度是2，因为需要改变 x x x 和 y y y 两个方向；
- 然后再在输入特征图上采样对应的点进行卷积运算。
偏移量的学习是利用插值算法，通过反向传播进行学习。
假设卷积核尺寸为3x3，卷积核定义为R={ ( − 1 , − 1 ) , ( − 1 , 0 ) , ( − 1 , 1 ) , ( 0 , − 1 ) , ( 0 , 0 ) , ( 0 , 1 ) , ( 1 , − 1 ) , ( 1 , 0 ) , ( 1 , 1 ) \\(-1,-1),(-1,0),(-1,1),\\ (0,-1),(0,0),(0,1),\\ (1,-1),(1,0),(1,1) (−1,−1),(−1,0),(−1,1),(0,−1),(0,0),(0,1),(1,−1),(1,0),(1,1)}，
它对应卷积核的9个采样点；设 x ( ) , y ( ) x(),y() x(),y() 分别是卷积层的输入输出特征图， w w w 是卷积核权值， p 0 p_0 p0 是滑动窗口中心点， p n p_n pn 是卷积核的采样点， Δ p n \Delta p_n Δpn 是网络中端到端学习到的。
则普通卷积的计算公式为：
y ( p 0 ) = ∑ p n R w ( p n ) ∗ x ( p 0 + p n ) y(p_0)=\sum_{p_n}^{R} w(p_n)*x(p_0+p_n) y(p0)=pn∑Rw(pn)∗x(p0+pn)
可变形卷积的计算公式为：
y ( p 0 ) = ∑ p n R w ( p n ) ∗ x ( p 0 + p n + Δ p n ) y(p_0)=\sum_{p_n}^{R} w(p_n)*x(p_0+p_n+\Delta p_n) y(p0)=pn∑Rw(pn)∗x(p0+pn+Δpn)
由于 Δ p n \Delta p_n Δpn 可能不是整数，所以会导致 p 0 + p n + Δ p n p_0+p_n+\Delta p_n p0+pn+Δpn 不在网格点上，此时需要采用双线性插值：
x ( p ) = ∑ q G ( q , p ) ∗ x ( q ) 其中 p = p 0 + p n + Δ p n ， q 是整数网格点 G ( q , p ) = ( 0 , 1 − ∣ q x − p x ∣ ) ∗ m a x ( 0 , 1 − ∣ q y − p y ∣ ) 是双线性插值 x(p)=\sum_{q}G(q,p)*x(q)\\其中p=p_0+p_n+\Delta p_n，q是整数网格点\\G(q,p)=(0,1-|q_x-p_x|)*max(0,1-|q_y-p_y|)是双线性插值 x(p)=q∑G(q,p)∗x(q)其中p=p0+pn+Δpn，q是整数网格点G(q,p)=(0,1−∣qx−px∣)∗max(0,1−∣qy−py∣)是双线性插值
二.1x1卷积的作用
1.实现信息的跨通道交互和整合
N I N （ N e t w o r k i n N e t w o r k ） NIN（Network in Network） NIN（NetworkinNetwork）通过在卷积层中使用 M L P MLP MLP 替代传统线性的卷积核，是单层卷积层内具有非线性映射的能力，它将不同通道的特征整合到 M L P MLP MLP 子网络中，让不同通道的特征能够交互整合，使通道之间的信息得以流通，其中的 M L P MLP MLP 子网络恰恰可以用 1x1 的卷积代替。
2.对卷积核通道数进行降维和升维，减小参数量
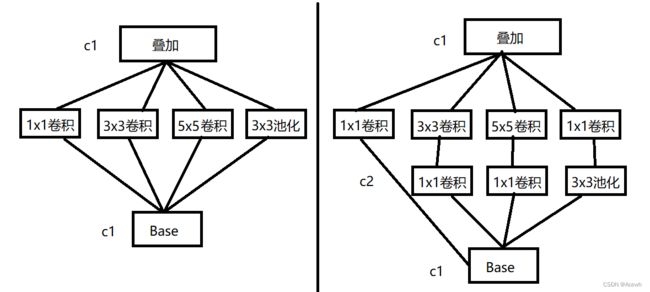
如上图所示，设模型的输入和出处都是 c 1 = 32 c1=32 c1=32 通道,而右图中的1x1卷积的通道数为 c 2 = 16 c2=16 c2=16，在不考虑偏置的情况下，则：
左半部分模型的参数量为：c1x(1x1+3x3+5x5)xc1=35840
右半部分模型的参数里为：c2x(1x1)xc1+ c1x(1x1)xc1x3 +c2x(3x3+5x5)xc1=20992
可见模型的参数量大大降低。
三.卷积核的大小
卷积核的大小越大越好还是越小越好？卷积核的大小没有绝对的优劣，一般要视情况而定，极大或极小的卷积核都是不合适的。卷积核太小只能分离卷积而不能对输入的原始特征进行有效组合，而极大的卷积通常会产生过多无意义的特征，从而浪费计算资源。通常情况下，通过堆叠较小的卷积核比直接采用单个较大的卷积核会更加有效；而较大的卷积核适用在自然语义处理浅层模型中。
四.每层卷积的卷积核尺寸种类
经典的神经网络一般都是堆叠式网络，每层仅用一个尺寸的卷积核，如 VGG 的结构，大量使用了 3x3 卷积层：
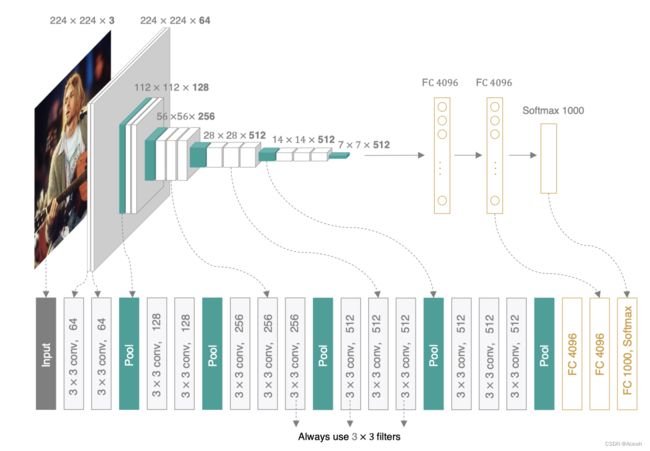
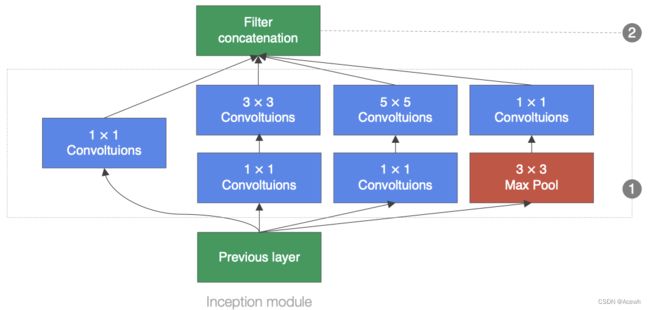
但是，同一层的特征图可分别使用不同尺寸的卷积核来提取不同尺度的特征，然后将它们结合起来，得到的特征要比前者好很多，比如 GooLeNet、Inception 系列网络，在同一层中分别使用了 1x1、3x3、5x5 的卷积核来提取特征，最后结合得到的特征图有更强的表达能力。
五.如何减少卷积层参数量
- 使用堆叠小卷积核代替大卷积核；
- 使用分离卷积：将 KxKxC 的卷积操作分离为 KxKx1 和 1x1xC 的两部分卷积操作；
- 添加1x1的卷积操作，改变通道数；
- 在卷积操作前添加池化操作。