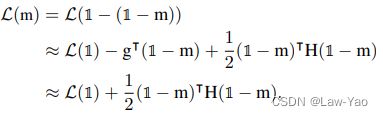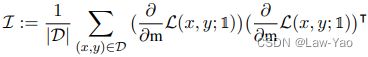Transformer模型的训练后剪枝方法

Paper地址：https://arxiv.org/abs/2204.09656

GitHub链接：https://github.com/WoosukKwon/retraining-free-pruning

前言

剪枝是一种经典的模型压缩方法，包括非结构剪枝、结构剪枝，它通过减少模型的冗余参数、以达到降低模型计算复杂度的目的。传统剪枝的实现方式包括训练感知方式（如Network Slimming、SFP、Taylor-prune等）与结构搜索方式（如NetAdapt、AMC等），包含三个阶段，即模型预训练、模型剪枝、模型重训练。因此传统剪枝的压缩成本相对较高，依赖训练资源、且训练的时间开销相对较高。

为了避免较重的训练开销，近年来训练后剪枝逐渐成为研究热点。类似于Post-training量化，仅需少量无标注数据的校准（特征对齐、最小化重建误差等校准方法），通过训练后压缩便能获得较好的压缩效果，且压缩成本可控（对训练资源的依赖较轻、时间代价也较低）。

Transformer模型因其特殊的模型结构（MHA+FFN），本文提出了针对性的训练后结构剪枝方法：1）基于Fisher信息设计Mask搜索算法（Mask search），寻找重要性最低的Attention heads或FFN neurons；2）通过Mask重排算法（Mask rearrangement），决定最终的（0-1取值）的剪枝Mask；3）基于少量无标注数据的知识蒸馏实现Mask微调（Mask tuning），获得Soft-mask以保持剪枝后模型的精度。

最终，针对BERT-base与DistilBERT，通过本文提出的训练后剪枝方法能够实现有效的结构剪枝，在GLUE与SQuAD数据集上，能够实现2x的FLOPS降解、1.56x的推理加速，精度损失低于1%；且在GPU单卡上，训练后剪枝的时间开销低于3分钟，实现过程非常轻量。

方法

剪枝过程可表示为受约束的优化问题（以剪枝Mask m作为变量）：

当剪枝Mask发生变化时，会引起Loss的变化，可以按Taylor展开式表示如下：

因此可以使用Hessian信息近似表示剪枝的优化目标，而Fisher信息又可以作为Hesssian信息的近似：

def collect_mask_grads(model, head_mask, neuron_mask, dataloader):
    head_mask.requires_grad_(True)
    neuron_mask.requires_grad_(True)

    handles = apply_neuron_mask(model, neuron_mask)

    model.eval()
    head_grads = []
    neuron_grads = []
    for batch in dataloader:
        for k, v in batch.items():
            batch[k] = v.to("cuda", non_blocking=True)

        outputs = model(head_mask=head_mask, **batch)
        loss = outputs.loss
        loss.backward()

        head_grads.append(head_mask.grad.detach())
        head_mask.grad = None

        neuron_grads.append(neuron_mask.grad.detach())
        neuron_mask.grad = None

    for handle in handles:
        handle.remove()
    head_mask.requires_grad_(False)
    neuron_mask.requires_grad_(False)

    head_grads = torch.stack(head_grads, dim=0)
    neuron_grads = torch.stack(neuron_grads, dim=0)
    return head_grads, neuron_grads


@torch.no_grad()
def compute_fisher_info(grads):
    fisher_info = grads.pow(2).sum(dim=0)
    return fisher_info

基于剪枝的优化目标，训练后剪枝方法总体包括三个阶段：

• 基于Fisher信息的Mask搜索算法：优化问题重新表示如下：

其中I为Fisher信息，表示Attention head或FFN Neuron的重要性。因此，针对给定的约束条件（FLOPS或Latency约束），通过最小化剪除的Attention heads与FFN Neurons的重要性，可实现剪枝Mask的搜索（初步确定0-1取值），以FLOPS作为约束的搜索算法如下（基于Latency的搜索算法详见论文）：

@torch.no_grad()
def search_mac(
    config,
    head_grads,
    neuron_grads,
    seq_len,
    mac_constraint,
):
    assert mac_constraint < 1

    num_hidden_layers = config.num_hidden_layers
    num_attention_heads = config.num_attention_heads
    intermediate_size = config.intermediate_size
    hidden_size = config.hidden_size
    attention_head_size = int(hidden_size / num_attention_heads)

    original_mac = compute_mac(
        [num_attention_heads] * num_hidden_layers,
        [intermediate_size] * num_hidden_layers,
        seq_len,
        hidden_size,
        attention_head_size,
    )
    max_mac = mac_constraint * original_mac

    head_importance = compute_fisher_info(head_grads)
    neuron_importance = compute_fisher_info(neuron_grads)

    # Globally rank heads and neurons
    sorted_head_importance, sorted_head_indicies = head_importance.view(-1).sort(descending=True)
    sorted_neuron_importance, sorted_neuron_indicies = neuron_importance.view(-1).sort(descending=True)

    max_importance = 0
    for num_heads in range(1, num_hidden_layers * num_attention_heads + 1):
        heads_mac = mac_per_head(seq_len, hidden_size, attention_head_size) * num_heads
        neurons_mac = max_mac - heads_mac
        num_neurons = int(neurons_mac / mac_per_neuron(seq_len, hidden_size))
        num_neurons = max(num_neurons, 0)

        total_importance = sorted_head_importance[:num_heads].sum() + sorted_neuron_importance[:num_neurons].sum()
        if total_importance > max_importance:
            max_importance = total_importance
            head_indicies = sorted_head_indicies[:num_heads]
            neuron_indicies = sorted_neuron_indicies[:num_neurons]

    head_mask = torch.zeros(num_hidden_layers * num_attention_heads).cuda()
    head_mask[head_indicies] = 1.0
    head_mask = head_mask.view(num_hidden_layers, num_attention_heads)

    neuron_mask = torch.zeros(num_hidden_layers * intermediate_size).cuda()
    neuron_mask[neuron_indicies] = 1.0
    neuron_mask = neuron_mask.view(num_hidden_layers, intermediate_size)

    return head_mask, neuron_mask

• Mask重排：为了进一步考虑相同Layer当中、不同Mask变量之间的相互影响，通过贪心算法实现了Mask变量的重排：

@torch.no_grad()
def greedy_rearrange(mask, grads):
    num_unpruned = int(mask.sum())
    num_pruned = mask.shape[0] - num_unpruned
    if num_unpruned == 0 or num_pruned == 0:
        return mask

    grads = grads.permute(1, 0).contiguous() # shape: [#heads/neurons, #mini_batches]
    grads_sq = grads.pow(2).sum(dim=1)
    _, indicies = grads_sq.sort(descending=False)
    indicies = indicies.tolist()

    # Greedy search
    masked_indicies = indicies[:num_pruned]
    for index in indicies[num_pruned:]:
        masked_indicies.append(index)
        grad_vectors = grads[masked_indicies]
        grad_sum = grad_vectors.sum(dim=0)

        complement = grad_sum - grad_vectors
        grad_sum_length = complement.pow(2).sum(dim=1)

        removed = grad_sum_length.argmin()
        del masked_indicies[removed]

    new_mask = torch.ones_like(mask)
    new_mask[masked_indicies] = 0
    return new_mask


def rearrange_mask(mask, grads):
    # NOTE: temporarily convert to CPU tensors as the arithmetic intensity is very low
    device = mask.device
    mask = mask.cpu()
    grads = grads.cpu()

    num_hidden_layers = mask.shape[0]
    for i in range(num_hidden_layers):
        mask[i] = greedy_rearrange(mask[i], grads[:, i, :])

    mask = mask.to(device)
    return mask

• Mask微调：基于少量无标注数据的知识蒸馏（以未剪枝模型作为Teacher，中间尺寸的模型作为助教），通过特征对齐方式实现（1-取值）的Mask变量的微调，从而获得Soft-mask以保持剪枝模型的识别精度：

实验结果

针对BERT-base与DistilBERT，训练后剪枝的压缩效果如下：