笔记：A Novel Representation of Parts for Accurate 3D Object Detection and Tracking in Monocular Images

A Novel Representation of Parts for Accurate 3D Object Detection and Tracking in Monocular Images
2015 IEEE International Conference on Computer Vision 文章地址

Abstract：We present a method that estimates in real-time and under challenging conditions the 3D pose of a known object. Our method relies only on grayscale images since depth cameras fail on metallic objects; it can handle poorly textured objects, and cluttered, changing environments; the pose it predicts degrades gracefully in presence of large occlusions. As a result, by contrast with the state-of-the-art, our method is suitable for practical Augmented Reality applications even in industrial environments. To be robust to occlusions, we first learn to detect some parts of the target object. Our key idea is to then predict the 3D pose of each part in the form of the 2D projections of a few control points. The advantages of this representation is three-fold: We can predict the 3D pose of the object even when only one part is visible; when several parts are visible, we can combine them easily to compute a better pose of the object; the 3D pose we obtain is usually very accurate, even when only few parts are visible.

1、文章提出了一种在具有挑战性的条件下实时估计已知对象的3D姿态的方法，该方法仅使用灰度图像进行预测。
2、为了在遮挡情况下保持方法的鲁棒性，首先学习检测目标对象的某些部分。关键思想是以几个控制点的2D投影预测每个part的3D姿态。 优点在于：即使只有一个part可见，也可以预测物体的3D姿态；当多个parts可见时，也可以很容易地将它们组合起来，以计算物体更准确的姿态。

1 Introduce

3D object detection and tracking methods have undergone impressive improvements in recent years [5, 27, 13, 4, 30, 25, 39, 17, 1, 45, 38, 20, 35, 44]. However, each of the current approaches has its own weaknesses: Many of these approaches [5, 13, 1, 35] rely on a depth sensor, which
would fail on metallic objects or outdoor scenes; methods based on feature points [25, 17] expect textured objects; those based on edges [4, 39] are sensitive to cluttered background; most of these methods [13, 27, 30, 38, 11, 45, 20] are not robust to occlusion. We also want a method fast enough for interactive 3D applications.
近年来，3D对象检测和跟踪方法已经取得了令人印象深刻的进步[5，27，13，4，30，25，39，17，1，45，38，20，35，44]。然而，目前的每一种方法都有自己的缺点：这些方法中的许多[5，13，1，35]依赖于深度传感器，这会在金属物体或户外场景中失败；基于特征点的方法[25，17]需要有纹理的对象；基于边缘的方法[4，39]对杂乱背景敏感；这些方法[13，27，30，38，11，45，20]中的大多数对遮挡不鲁棒。我们还需要一种足够快的方法用于交互式3D应用程序。

图1：在具有挑战性的条件下，用常规相机检测3D的盒子。在该数据集上，用户从盒子中取出物品，并将它们放在桌面上，通常情况下会遮挡大部分盒子。尽管存在这些困难，但我们可以在每个图像中独立准确地估计盒子的3D姿态。

As Fig. 1 shows 1, we are interested in scenes with poorly textured objects, possibly visible only under heavy occlusions, drastic light changes, and changing background. A depth sensor is not an option in our setup, as the target objects often have specular surfaces. Feature point-based methods also fail because of the lack of texture. These are typical conditions of many Augmented Reality applications.
如图1所示，我们对纹理较模糊的物体感兴趣，这些物体可能仅在严重遮挡、剧烈光线变化和背景变化的情况下可见。深度传感器不在我们设置的选项中，因为目标对象通常具有镜面。由于缺少纹理，基于特征点的方法也会失败。这些是许多增强现实应用的典型条件。

At the core of our approach is the efficient detection of discriminative parts of the target object. Relying on parts for 3D object detection is not new [12, 27, 33, 20, 45]. The novelty in our approach is a powerful representation of the pose of each part.
我们方法的核心是有效检测目标对象具有识别性的part，[12、27、33、20、45]也应用了类似的方法。 我们方法的创新性在于对每个part姿势的有效表示。

Some previous methods used homographies [16, 12, 45] to represent a part pose, however this assumes that the object is piece-wise planar, and it is not easy to combine the homographies from several parts together to compute a better pose for the target object. Feature point-based methods
simply use the 2D locations of the feature points, which wastes very useful information.
以前的一些方法使用单应图[16，12，45]来表示part的姿态，然而这些方法假设对象是逐段平面的，并且不容易将多个部分的单应图组合在一起以计算目标对象的更好姿态。基于特征点的方法简单地使用特征点的2D位置，浪费了非常有用的信息。

图2.对物体part的三维姿态的表示。（a）每个part设置七个3D控制点，这些控制点排列成三个正交方向。（b）给定物体part的图像块，使用回归器预测这些控制点的2D重投影，以及预测的不确定性。

As shown in Fig 2, we therefore propose to represent the pose of each part by the 2D reprojections of a small set of 3D control points. The control points are only“virtual”, and do not have to correspond to specific image features. This representation is invariant to the part’s image location and only depends on its appearance. We show that a Convolutional Neural Network [19] (CNN) can predict the locations of these reprojections very accurately, and can also be used to predict the uncertainty of these location estimates.
如图2所示，我们建议通过一小组3D控制点的2D重投影来表示每个part的姿态。控制点只是“虚拟”的，不必与特定的图像特征相对应。该表示对于part的图像位置是不变的，并且仅取决于其外观。 我们表明，卷积神经网络[19]（CNN）可以非常准确地预测这些重投影的位置，也可以用于预测这些位置估计的不确定性。

Given an input image, we run a detector to obtain a few hypotheses on the image locations of each part. We also use a CNN for this task, but another detection method could be used. We then predict the reprojections of the control points by applying a specific CNN to each hypothesis. This gives us a set of 3D-2D correspondences, some of which may be erroneous, but from which we can compute the 3D pose of the target object with a simple robust algorithm.
给定一个输入图像，我们运行一个检测器来获得关于每个part的图像位置的假设。 我们也使用CNN来完成这项任务，但也可以使用另一种检测方法。然后，我们通过对每个假设位置应用特定的CNN来预测控制点的2D重投影。 这为我们提供了一组3D-2D对应关系，其中一些可能是错误的，但从中我们可以使用简单的鲁棒算法计算目标对象的3D姿态。

This approach has several advantages:
• We do not need to assume the parts are planar, as was done in some previous work;
• we can predict the 3D pose of the object even when only one part is visible;
• when several parts are visible, we can combine them easily to compute a better pose of the object;
• the 3D pose we obtain is usually very accurate, even when only few parts (or a single one) are visible.
这种方法有几个优点：
•我们不需要假设每part都是平面的，就像之前的一些工作中所做的那样；
•即使只有一part可见，我们也可以预测物体的3D姿态；
•当多个parts可见时，我们可以很容易地将它们组合起来，以计算对象的更佳姿态；
•即使只有少数part（或单个part）可见，我们获得的3D姿态通常也非常准确。

2 Related Work

略

3 Part Pose Representation and Estimation

Given an input grayscale image2, we want to estimate the 3D pose p of a calibrated projective camera with respect to a known rigid object. We assume that we are given a 3D model of the object, for example in the form of a triangular mesh, and a set of manually labelled parts on the object. A very small number of parts is required by our framework; in all our tests we employed at most 4 parts for an object. We currently select the parts by hand (automatic selection is left to future work). Ideally, the parts should be easy to detect in images, and spread over the object.
给定输入灰度图像（所有实验都使用VGA图像），我们希望估计校准投影相机相对于已知刚性物体的3D姿态p。我们假设我们得到了物体的3D模型，例如，三角形网格的形式，以及物体上一组手动标记的part。我们的框架需要非常少的part；在我们的所有测试中，一个物体最多使用4个part。我们目前手动选择物体被识别的part（自动选择留待将来的工作）。理想情况下，这个部分应易于在图像中检测，并扩展到整个物体。

In this section, we justify our choice for the representation of the pose parts, and we explain how we detect the parts and predict their poses. The next section describes our algorithm to compute the pose of the camera based on the predicted pose parts. The main notations are resumed in Table 1.
在本节中，我们证明了我们对用于姿态表示的part的选择，并解释了我们如何检测这些parts并预测它们的姿态。下一节描述了基于已预测的part姿势来计算相机姿势的算法。表1中列出了主要符号。

3.1. Representing the Part Poses

One can think of different ways to represent the 3D poses of parts of objects. For example, it is possible to use homographies [16, 12, 45]. However, this assumes that the part surface is planar, and makes it difficult to merge the contributions of the different parts.
人们可以想到不同的方法来表示物体的部分3D姿态。例如，可以使用单应图[16，12，45]。但是，这些文章假设part表面是平面的，因此很难合并不同的part。

Another possibility we considered is to predict from the appearance of the part, a 3D rotation matrix and the depth value of its center. Assuming an orthogonal projection, it is possible to retrieve the 3D translation as well, from the patch center image location and the predicted depth. However, this representation is not translation invariant in a full perspective model. Also it is not clear how to merge rotations for estimating the pose of the whole target object. Finally, it is difficult to predict the depth accurately from the image patch, as our results will demonstrate.
我们考虑的另一种可能的方法是从物体的外观、3D旋转矩阵及其中心的深度值来估计。假设正交投影，也可以从补丁中心图像位置和预测的深度值检测3D平移。然而，这种表示在全透视模型中不是平移不变的。此外，还不清楚如何合并旋转以估计整个目标物体的姿态。最后，如我们的结果所示，很难从图像块准确预测深度。

Since ourfinal solution is based on 3D control points, as already mentioned, we could also directly predict the 3D locations of the 3D Control Points in the camera reference system: This makes combining the poses simpler, as this only involves computing the rigid motion between two sets of 3D points [40]. Unfortunately, this representation is not translation invariant. Moreover, as for the previous option, it requires to directly predict the depths of the points, which is far from accurate in our experiments.
由于我们的最终解决方案基于3D控制点，如前所述，我们还可以直接预测相机参考系统中3D控制点的3D位置：这使得组合姿势更简单，因为这只涉及计算两组3D点之间的刚性运动[40]。不幸的是，这种表示不是平移不变的。此外，对于前面的选项，它需要直接预测点的深度，这在我们的实验中远远不够准确。

This is why we propose to represent the part pose as the 2D reprojections of a set of 3D control points. This representation is fully translation invariant; it is straightforward to combine the poses of an arbitrary number of parts, by simply grouping all the 2D reprojections together and solving a PnP problem; we do not need to predict the depth of the 3D points, which is difficult to do accurately. These advantages entail a tremendous accuracy gain, as showed by our results in Section 5.2. In our experiments, we used 7 control points for each part, spanning 3 orthogonal directions, as shown in Fig. 2(a), however other configurations could probably be used.
这就是为什么我们计划将part姿态表示为一组3D控制点的2D重投影。这种表示是完全平移不变的；通过将所有2D重投影简单地组合在一起并求解PnP问题，可以简单地组合任意数量的part的姿态；我们不需要预测3D点的深度，这很难准确地做到。如我们在第5.2节中的结果所示，这些优势带来了巨大的精度增益。在我们的实验中，我们为每个部件使用了7个控制点，跨越3个正交方向，如图2（a）所示，但也可能使用其他配置。

3.2. Detecting the Parts

图3.检测part.（a） 盒子的输入图像。（b） 每个图像位置的$CN{N}^{part-det}$的输出。每种颜色对应不同的part。（c） 高斯平滑后的输出。（d） 检测到的部分，对应于（c）中的局部最大值

We use a set of registered training images of the target object under different poses and lighting (as the one shown in Fig. 3(a)) to learn to detect the parts and predict their control points. We will denote our training data as:
我们使用目标物体在不同姿态和照明下的一组训练图像（如图3（a）所示）来学习检测part并预测其控制点。我们将训练数据表示为
$$T=\{(I_i,\{c_{ij}{\}}_j,\{v_{ijk}{\}}_{jk}{\}}_i,$$
where $I_i$denotes the i-th training image, $c_{ij}$ the projectionof the center $C_j$ of the $j_{th}$ part on $I_i$, and $v_{ijk}$ the projection of the $k_{th}$ control point of the $j_{th}$ part in this image.
其中$I_i$表示第$i$个训练图像，$c_{ij}$表示第$j$个部分的中心$C_j$ 在$I_i$上的投影，$v_{ijk}$表示该图像中第$j$个part的第k个控制点的投影。

图4.用于part检测的$CN{N}^{part-det}$架构。最后一层输出与每个part或背景相对应的图像块的似然性。

During an offline stage, we train afirst CNN with a standard multi-class architecture shown in Fig. 4 to detect the parts. The input to this CNN is a 32 × 32 image patch $\mathbf{q}$, its output consists of the likelihoods $P(J=j|\mathbf{q})$ of the patch to correspond to one of the $N_P$ parts. We train the CNN with patches randomly extracted around the centers $c_{ij}$ of the parts in images $I_i$ and patches extracted from the background, and by optimizing the negative log-likelihood over the parameters $\omega$ of the CNN:
在离线阶段，我们使用图4所示的标准多类架构训练第一个CNN，以检测part。该CNN的输入是一个32×32的图像块 $\mathbf{q}$，其输出由对应于$N_P$ parts之一的图像块的似然性$P(J=j|\mathbf{q})$组成。我们使用围绕图像$I_i$中的part的中心$c_{ij}$随机提取的图像块和从背景中提取的图像块来训练CNN，并通过优化CNN的参数$\omega$上的负对数似然性：
$$\hat{\omega }=argmin\sum _{j=0}^{N_P}\sum _{\mathbf{q}\in T_j}-logsoftmax(CN{N}_{\omega }^{part-det}(\mathbf{q}))[j]$$
where $T_j$ is a training set made of image patches centered on part $j$ and $T_0$ is a training set made of image patches from the background, $CN{N}_{\omega }^{part-det}(\mathbf{q})$ is the $N_P+1$-vector output by the CNN when applied to patch $\mathbf{q}$, and softmax$CN{N}_{\omega }^{part-det}(\mathbf{q})[j]$ is the j-th coordinate of vector softmax$CN{N}_{\omega }^{part-det}(\mathbf{q})$.
其中，$T_j$是由以part $j$为中心的图像块组成的训练集， $T_0$是由来自背景的图像块构成的训练集。$CN{N}_{\omega }^{part-det}(\mathbf{q})$是当应用于图像块$\mathbf{q}$时由CNN输出的$N_P+1-vector$，$CN{N}_{\omega }^{part-det}(\mathbf{q})[j]$是矢量softmax的第$j$个坐标$CN{N}_{\omega }^{part-det}(\mathbf{q})$。

At run time, we apply this CNN to each 32 × 32 patch in the input images captured by the camera. This can be done very efficiently as the convolutions performed by the CNN can be shared between the patches [9]. As shown in Fig. 3, we typically obtain clusters of large values for the likelihood of each part around the centers of the parts. We therefore apply a smoothing Gaussianfilter on the output of the CNN, and retain only the local maximums of these values as candidates for the locations of the parts.
在运行时，我们将此CNN应用于相机捕获的输入图像中的每个32×32小块。这可以非常有效地完成，因为CNN执行的卷积可以在图像块之间共享。如图3所示，我们通常获得围绕part中心的每个part的似然性的大值聚类。因此，我们在CNN的输出上应用平滑高斯滤波器，并仅保留这些值的局部最大值作为零件位置的候选值。

The result of this step is, for each part $j$, a set $S_j={({\hat{c}}_{jl},s_{jl})}_l$ of 2D location candidate ${\hat{c}}_{jl}$ for the part together with a score $s_{jl}$ that is the value of the local maxima returned by the CNN. We will exploit this score in our pose estimation algorithm described in Section 4. We typically get up to 4 detections for each part in a given input image.
该步骤的结果是，对于每个部分 $j$，该部分的2D位置候选的集合$S_j={({\hat{c}}_{jl},s_{jl})}_l$以及分数$s_{jl}$，该分数$s_{jl}$是CNN返回的局部最大值的值。我们将在第4节中描述的姿态估计算法中利用这个分数。我们通常对给定输入图像中的每个part进行最多4次检测。

3.3. Predicting the Reprojections of the Control Points and their Uncertainty

Once the parts are detected, we apply a second CNN to the patches centered on the candidates ${\hat{c}}_{jl}$ to predict the projections of the control points for these candidates. Each part has its specific CNN. As shown in Fig. 5, these networks take as input a patch of size of 64 × 64. The output layer is made of 2$N_V$ neurons, with $N_V$ the number of control points of the part, which predicts the 2D locations of the control points. We train each of these CNNs during an offline stage by simply minimizing over the parameters $\omega$ of the CNN the squared loss of the predictions:
一旦检测到物体的part，我们将第二个CNN应用于以候选点${\hat{c}}_{jl}$为中心的图像块，以预测这些候选控制点的投影。每个part都有其特定的CNN。如图5所示，这些网络将大小为64×64的区域作为输入。输出层由2$N_V$个神经元组成，用来预测控制点的2D位置，$N_V$是part中控制点的数量。我们在离线阶段通过简单地最小化CNN的参数$\omega$来训练这些CNN中的每一个预测的平方损失：
$$\hat{\omega }=arg\min \sum _{(\mathbf{q},\mathbf{w})\in V_j}||\mathbf{w}-CN{N}_{\omega }^{cp-pred-j}(\mathbf{q})|{|}^2$$
where $V_j$ is a training set of image patches $\mathbf{q}$ centered on part $j$ and the corresponding 2D locations of the control points concatenated in a (2$N_V$)-vector $\mathbf{w}$, and $CN{N}_w^{cp-pred-j}(\mathbf{q})$ is the prediction for these locations made by the CNN specific for part $j$, given patch $\mathbf{q}$ as input.
其中$V_j$是以part $j$为中心的图像块$\mathbf{q}$的训练集，以及以(2$N_V$)的向量$\mathbf{w}$连接的控制点的对应2D位置，并且$CN{N}_w^{cp-pred-j}(\mathbf{q})$ 是给定图像块$\mathbf{q}$作为输入，CNN对part $j$做出的位置预测。

At run-time, we obtain for each ${\hat{c}}_{jl}$ candidate, predictions $\{{\hat{v}}_{jkl}\}$ for the control points projections. In addition, we estimate the 2D uncertainty for the predictions, by propagating the image noise through the CNN that predicts the control point projections . Let us consider the matrix:
在运行时，我们获得了每个候选的控制点${\hat{c}}_{jl}$的预测$\{{\hat{v}}_{jkl}\}$。此外，我们通过通过预测控制点投影的CNN传播图像噪声来估计预测的2D不确定性[43]。让我们考虑以下矩阵：
$$S_V=J_{\hat{c}}(\sigma I)J_{\hat{c}}^{\top }(4)$$

where $\sigma$ is the standard deviation of the image noise assumed to be Gaussian and affect each image pixel independently, $I$ is the $64^2\times 64^2$ Identity matrix, and $J_{\hat{c}}$ is the Jacobian of the function computed by the CNN, evaluated at the patch centered on the candidate $\hat{c}$. Such a Jacobian matrix can be computed easily with a Deep Learning framework such as Theano, by composing the Jacobians of the successive layers of the network. We neglect the correlation between the different control points tofinally extract from the block diagonal of $S_V$ the 2 × 2 uncertainty matrix noted $S_{jkl}$ below for each control point. An example of predicted control points and their uncertainties is shown in Fig. 2(b). Note that we can easily compute the $S_{jkl}$ matrices without having to compute the entire, and very large, product in Eq. (4)
其中σ是假设为高斯并独立影响每个图像像素的图像噪声的标准偏差，$I$为$64^2\times 64^2$恒等矩阵，$J_{\hat{c}}$ 为CNN计算的函数的雅可比矩阵，在以候选点为中心的图像块处进行评估。通过组合网络的连续层的雅可比矩阵，可以使用深度学习框架（如Theano）轻松计算此类雅可比矩阵。我们忽略了不同控制点之间的相关性，最终从$S_V$的块对角线中提取每个控制点的2×2。预测控制点及其不确定性的示例如图2（b）所示。注意，我们可以很容易地计算$S_{jkl}$矩阵，而不必计算公式（4）中的整个非常大的乘积。

4. Estimating the Object Pose

Thanks to our representation for the part poses, estimating the object pose is straightforward, since each control point provides a 3D-2D correspondence. We describe here the method we use, other methods are probably possible.
由于我们对part姿态的表示，使得估计物体姿态很简单，因为每个控制点都提供了3D-2D对应关系。我们在这里描述我们使用的方法，其他方法也可能有效。

We assume that we are given a prior on the pose $\mathbf{p}$, in the form of a Mixture-of-Gaussians$\{({\bar{p}}_m,S_m)\}$, as [23] was done e.g. in. This prior is very general, and allows us to define the normal action range of the camera. Moreover, the pose computed for the previous frames can be easily incorporated within this framework to exploit temporal consistency.
我们假设我们以Mixture-of-Gaussian$\{({\bar{p}}_m,S_m)\}$的形式给出了姿态$\mathbf{p}$的先验，如[23]中所做的。这个先验是非常通用的，允许我们定义相机的正常动作范围。此外，为先前帧计算的姿态可以容易地并入这个框架中，以利用时间一致性。

In the following, we willfirst assume that this prior is defined as a single Gaussian distribution of mean and covariance $({\bar{p}}_0,S_0)$. We will extend our approach to the Mixture-of-Gaussians in Section 4.3.
在下文中，我们将首先假设该先验被定义为均值和协方差$({\bar{p}}_0,S_0)$的单一高斯分布。我们将在第4.3节中将我们的方法扩展到Mixture-of-Gaussians。

4.1. Using a single Gaussian Pose Prior

Let usfirst assume there is no outlier returned by the part detection process or by the control point prediction, and that all the parts are visible. Then, the object pose $\hat{p}$, or equivalently the camera pose, can be estimated as the minimizer of $F(p)$, with $F(p)$=
让我们首先假设part检测过程或控制点预测没有返回异常值，并且所有部分都是可见的。然后，可以将物体姿态（或等效的相机姿态）估计为$F(p)$的最小值，其中$F(p)$=
$$\frac{1}{N_P}\sum _{j,k}dis{t}^2(S_{jk},\Gamma p(V_{jk}),{\hat{v}}_{jk})+(\mathbf{p}-{\bar{\mathbf{p}}}_0)\top S_0^{-1}(\mathbf{p}-{\bar{\mathbf{p}}}_0)(5)$$

where the sum is over all the control points of all the parts, and $\Gamma p(V)$ is the 2D projection of V under pose $p.{\hat{v}}_{jk}$ is the projection of control point $V_{jk}$ and $S_{jk}$ its uncertainty estimated as explained in Section 3.3—since we assume there is no outlier, we dropped here the l index corresponding to the multiple detections. dist(.) is the Mahalanobis distance:
其中，和在所有部分的所有控制点上，$\Gamma p(V)$是$V$在姿态$p$下的2D投影。 ${\hat{v}}_{jk}$是控制点$V_{jk}$和$S_{jk}$的投影，其不确定性如第3.3节所述 ——因为我们假设没有异常值，所以我们在这里删除了与多次检测相对应的$l$。dist（.）是马氏距离。

$F(p)$ is minimized using the Gauss-Newton algorithm initialized with $p_0$.
$F(p)$使用初始化为$p_0$的高斯-牛顿算法最小化。

4.2. Robust detection of parts

In practice, for the location of the $j_{th}$ part, the detection procedure described in Section 3.2 can get a set of hypotheses $S_j$, and at most one is correct.
实际上，对于第$j$部分的位置，第3.2节中描述的检测程序可以得到一组假设$S_j$，并且最多有一个是正确的。

Checking all the possible combinations would be time consuming, so we rank the candidates according to their score $s_{jl}$, keep the best four candidates for each part and greedily examine the possible sets $C$ of correspondences between a part and the candidate detections.
检查所有可能的组合将是耗时的，因此我们根据候选部分的分数$s_{jl}$对其进行排名，为每个part保留最好的四个，并使用贪婪算法检查一个部分和候选检测之间的可能的对应集合$C$。

Similarly to [23], we exploit the pose prior forfirst quickly evaluating if the correspondences in $C$ can yield a good pose estimate.
类似于[23]，我们利用先验姿态，首先快速评估 $C$ 中对应的姿态是否能够产生良好的姿势估计。

We only consider a set $C$ if

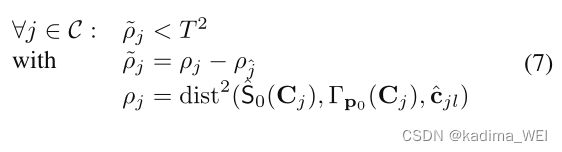
where $T=40$, and where${\hat{S}}_0(C_j)=J{S}_0{J}^{\top }$, with $J$ the jacobian of ${\Gamma }_{p_0}(C_j)$, is the covariance of the projection ${\Gamma }_{p_0}(C_j)$ of $C_j$, and $p_{\hat{j}}$ is a random candidate of the set (since it is reasonable to suppose that at least one candidate of a part has been reliably detected).
其中$T=40$，且其中${\hat{S}}_0(C_j)=J{S}_0{J}^{\top }$，其中$J$是${\Gamma }_{p_0}(C_j)$的雅可比，是$C_j$的投影${\Gamma }_{p_0}(C_j)$的协方差，$p_{\hat{j}}$是集合的随机候选（因为有理由假设至少一个part的候选控制点已经被可靠地检测到）。

If $C$ passes this test, we compute the average distance$\bar{\rho }=\frac{1}{|C|}{\sum }_j{\rho }_j^{\sim }$ of its points. We keep the $N_C$ sets with the lowest average distance (in practice, we set $N_C=4$ for all our experiments); we run the Gauss-Newton optimization of Eq. (5) using each $C$ to obtain a pose estimate, and evaluate it as explained in Section 4.3.
如果 $C$ 通过该测试，我们计算平均距离$\bar{\rho }=\frac{1}{|C|}{\sum }_j{\rho }_j^{\sim }$。我们保持具有最低平均距离的$N_C$集（在实践中，我们为所有实验设置了$N_C=4$）；我们使用每个 $C$ 运行方程（5）的高斯-牛顿优化，以获得姿态估计，并按照第4.3节所述对其进行评估。

4.3. Using a Mixture-of-Gaussians for the Pose Prior

In practice, the prior for the pose is in the form of a Mixture-of-Gaussians {(pm,Σm)}m with M = 9 components (the prior employed for the BOX dataset is shown in Fig.6). We apply the method described above to each
component, and obtain $M{N}_C$ possible pose estimates:${\hat{p}}^{(1)},...,{\hat{p}}^{(}M{N}_C)$.
在实践中，姿态的先验是Mixture-of-Gaussians$\{(p_m,{\sum }_m){\}}_m$与 $m=9$ 个分量的混合形式（BOX数据集使用的先验如图6所示）。我们将上述方法应用于每个分量，并获得$M{N}_C$可能的姿态估计：${\hat{p}}^{(1)},...,{\hat{p}}^{(}M{N}_C)$。

To finally identify the best pose estimate, we evaluate each${\hat{p}}^{(n)}$, employing a weighted sum of several cues: the angle between the quaternions for${\hat{p}}^{(n)}$and the corresponding ${\bar{p}}_m$ prior; the average reprojection error of the set of
control points C according to ${\hat{p}}^{(n)}$; the correlation between the object contours after projection by ${\hat{p}}^{(n)}$ and the edges detected in the image. For setting the weights, we train a simple linear regressor on the training video sequences to predict the Euclidean distance between ${\hat{p}}^{(n)}$and the groundtruth. At testing time, we use the linear regressor to evaluate the quality of the computed pose, i.e we keep the pose that gives the smallest predicted distance.
为了最终确定最佳姿态估计，我们使用几个线索的加权和来评估每个${\hat{p}}^{(n)}$：${\hat{p}}^{(n)}$的四元数与相应的${\bar{p}}_m$先验之间的角度；控制点C的集合的平均重投影误差，根据${\hat{p}}^{(n)}$；投影后的物体轮廓与图像中检测到的边缘之间的相关性。为了设置权重，我们在训练视频序列上训练一个简单的线性回归器，以预测${\hat{p}}^{(n)}$和地面真相之间的欧几里得距离。在测试时，我们使用线性回归器来评估计算出的姿势的质量，即我们保持给出最小预测距离的姿势。

If the optimization of Eq. (5) converges, we add to the initial prior the estimated pose and its covariance as part of the pose prior for the next frame. This helps enforcing temporal consistency. The pose covariance is obtained using the Extended Kalman Filter update formula [43] when optimizing Eq. (5).
如果等式（5）的优化收敛，我们将估计的姿态及其协方差作为下一帧的姿态先验的一部分添加到初始先验。这有助于加强时间一致性。当优化方程（5）时，使用扩展卡尔曼滤波器更新公式[43]获得姿态协方差。

5. Experimental Results