前馈神经网络与支持向量机实战 --- 手写数字识别
前馈神经网络与支持向量机实战 — 手写数字识别
文章目录
- 前馈神经网络与支持向量机实战 --- 手写数字识别
-
- 一、前馈神经网络介绍
- 二、支持向量机介绍
- 三、数据集说明
- 四、环境准备
- 五、实验要求
- 六、Python代码
-
-
- tutorial_minst_fnn-keras.py:使用TensorFlow的Sequential实现的前馈神经网络
- tutorial_minst_fnn-tf2.0.py:使用TensorFlow的基础功能实现前馈神经网络
- SVM_sklearn.py:使用sk-learn实现支持向量机
- tutorial_minst_fnn-numpy.py:手写实现前馈神经网络(仅使用numpy,包括手写反向传播算法求解过程)
- SVM_manual.py:手写支持向量机(包括支持向量机的优化算法——SMO算法)
-
- 七、实验结果分析
一、前馈神经网络介绍
前馈神经网络(feedforward neural network,FNN),是一种最简单的神经网络,各神经元分层排列,每个神经元只与前一层的神经元相连。接收前一层的输出,并输出给下一层,各层间没有反馈,信号从输入层向输出层单向传播。
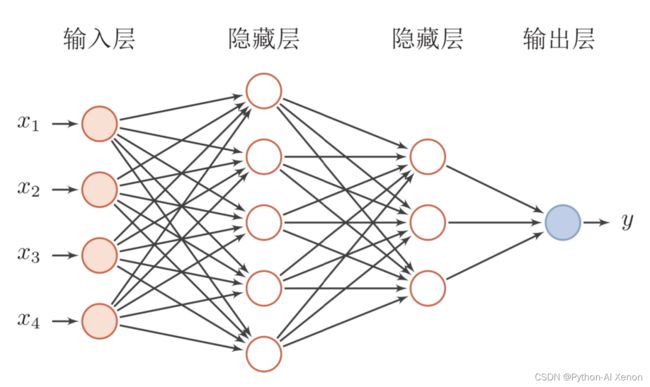
前馈神经网络采用一种单向多层结构。其中每一层包含若干个神经元。在此种神经网络中,各神经元可以接收前一层神经元的信号,并产生输出到下一层。第0层叫输入层,最后一层叫输出层,其他中间层叫做隐含层(或隐藏层、隐层)。隐层可以是一层。也可以是多层 。
一个典型的多层前馈神经网络如下图所示:
对于前馈神经网络结构设计,通常采用的方法有3类:直接定型法、修剪法和生长法。
关于神经网络的知识其实很多,这里也不展开进行叙述了.
⭐⭐⭐⭐⭐推荐参考书籍: 神经网络与深度学习nndl-book .
(邱锡鹏教授的《神经网络与深度学习》一书较全面地介绍了神经网络、机器 学习和深度学习的基本概念、模型和方法,同时也涉及深度学习中许多最新进 展.书后还提供了相关数学分支的简要介绍,以供读者需要时参考)
二、支持向量机介绍
支持向量机(Support Vector Machine, SVM)是一类按监督学习(supervised learning)方式对数据进行二分类的广义线性分类器(generalized linear classifier),其决策边界是对学习样本求解的最大边距超平面(maximum-margin hyperplane)
简单来说, 支持向量机(SVM)是一种求解二分类问题的算法,其核心思想为使用一线 性超平面将两类样本分开并使得两类样本与该超平面间的“间隔”最大。
对于非线性可分(无法找到可将两类样本分开的超平面)的样本集。SVM 采用核技巧将样本映射到更高维的空间上。已经证明,存在原样本空间到希尔伯特 空间的一个映射,使样本线性可分。
对于分类( > 2)的问题,可以采用训练多个 SVM 的方式解决,其中常用的方法有:
-
一类 VS 其它类(OVR)
即: 训练 − 1个 SVM,第个 SVM 用于分类是第个类别还是其它类别。
-
一类 VS 另一类(OVO)
即: 对任意两个类别都训练一个 SVM,共需n 2个分类器,一个样本将通过所有分类器,最终将样本决策为结果最多的类别。
同样,过多的深入的内容也不在此进行赘述了,感兴趣的可参考以下文章:
机器学习:支持向量机(SVM)
【数之道】支持向量机SVM是什么,八分钟直觉理解其本质
【机器学习】支持向量机 SVM
三、数据集说明
MNIST数据集(Mixed National Institute of Standards and Technology database)是美国国家标准与技术研究院收集整理的大型手写数字数据库,是机器学习领域中非常经典的一个数据集,由60000个训练样本和10000个测试样本组成,每个样本都是一张28 * 28像素的灰度手写数字图片。
- 官方网站 http://yann.lecun.com/exdb/mnist/
- 一共4个文件,训练集、训练集标签、测试集、测试集标签
| 文件名称 | 大小 | 内容 |
|---|---|---|
| train-images-idx3-ubyte.gz | 9,681 KB | 55000张训练集 |
| train-labels-idx1-ubyte.gz | 29 KB | 训练集图片对应的标签 |
| t10k-images-idx3-ubyte.gz | 1,611 KB | 10000张测试集 |
| t10k-labels-idx1-ubyte.gz | 5 KB | 测试集图片对应的标签 |
数据集的导入: (下面模块中均包含有该数据集)
四、环境准备
以下是我的运行环境(供参考)
- Python 3.9.13 (其它与tensorflow对应版本均可)
- PyCharm 2022.3 (Professional Edition)
- jupyter notebook (备选)
- tensorflow-gpu==2.10.0 (使用GPU进行加速,需单独安装该版本,详见下面文档)
- cuDNN==8.1 (tensorflow-gpu显卡依赖)
- CUDA==11.2 (tensorflow-gpu显卡依赖)
- numpy==1.23.3 (python科学计算库)
官方TensorFlow安装文档 (安装必看)
五、实验要求
1.使用TensorFlow的Sequential实现前馈神经网络,并完成手写数字识别任务。
包括数据集的读取,模型的建立,模型的训练,模型的测试。
2.使用TensorFlow的基础功能实现前馈神经网络,并完成手写数字识别任务。
包括数据集的读取,模型的建立,计算损失、准确性等功能的实现,使用梯度带完成模型的训练,模型的测试。
3.使用sk-learn实现支持向量机,并完成手写数字识别任务。
包括数据集的读取,模型的建立,模型的训练,模型的测试
4.手写实现前馈神经网络(仅允许使用numpy,需要手写反向传播算法求解过程)
- 其重点是手写反向传播算法,可以在对预测结果取log时,记下取log前的结果,便于求解交叉熵损失函数的导数。在求解softmax函数的导数时,也可以将求导结果中的对角阵与外积分别根据链式法则乘以之前的结果(交叉熵损失函数的导数)。手写完后,需要与TensorFlow的反向传播算法对比一下。
- 参考 GitHub - nndl/nndl-exercise-ans: Solutions for nndl/exercise
2.手写支持向量机(包括支持向量机的优化算法——SMO算法)
- 支持向量机不能用常规算法进行优化,但可以使用特有的优化算法:SMO算法。
- 参考 知乎专栏:支持向量机(SVM)——SMO算法
具体的分析及说明见下面代码注释.
六、Python代码
tutorial_minst_fnn-keras.py:使用TensorFlow的Sequential实现的前馈神经网络
# -*- coding: utf-8 -*-
# @Author : Xenon
# @Date : 2022/12/3 23:55
# @IDE : PyCharm(2022.2.3) Python3.9.13
"""使用TensorFlow的Sequential实现前馈神经网络"""
import os
import tensorflow as tf
from tensorflow import keras
from keras.datasets import mnist
from tensorflow.python.keras import layers
from keras.api.keras import optimizers
# from tensorflow.keras import layers, optimizers, datasets 该导入方式虽然会报错但也能正常运行
# from keras.api.keras import layers 也可选择该方式导入layers
# 设置log信息等级 INFO(通知0)
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '1' # or any {'0', '1', '2','3'}
def mnist_dataset():
"""读取TensorFlow自带的mnist手写字体数据集。
:return:训练集ds, 测试集test_ds(使用TensorFlow的dataset形式)
"""
# 从训练集提取20000个数据(共60000个)
(x, y), (x_test, y_test) = mnist.load_data() # 加载MNIST数据集。
# 创建一个数据集,其元素是给定张量的切片。切片2维张量生成1维张量元素。
ds = tf.data.Dataset.from_tensor_slices((x, y))
# 将数据打乱顺序并分成200个batch,每个batch有100个样本。
ds = ds.map(prepare_mnist_features_and_labels) # 将map_func映射到此数据集的元素
ds = ds.take(20000).shuffle(20000).batch(100) # 装载20000数据集打乱后分为100批
# 从测试集提取全部20000个数据,prepare_mnist_features_and_labels,打乱顺序,设置为1个batch
test_ds = tf.data.Dataset.from_tensor_slices((x_test, y_test))
test_ds = test_ds.map(prepare_mnist_features_and_labels)
test_ds = test_ds.take(20000).shuffle(20000).batch(20000)
return ds, test_ds
def prepare_mnist_features_and_labels(x, y):
"""
将x转化成TensorFlow的32位浮点数(tf.float32),并除以255.0,
将y转化成TensorFlow的64位整数(tf.int64)
:param x: 原始张量x
:param y: 原始张量y
:return: x,y (dtype新类型)
"""
# 将张量强制转换为dtype新类型
x = tf.cast(x, tf.float32) / 255.0
y = tf.cast(y, tf.int64)
return x, y
if __name__ == '__main__':
# 创建顺序模型实例。形参:layers–要添加到模型中的图层的可选列表。name–模型的可选名称
model = keras.Sequential([
# 将输入值转换成一维向量,注意:该层是对数据的一种处理,在算法上并不认为是一层。
layers.Reshape(target_shape=(28 * 28,)),
# 第一隐含层,全连接层,100个神经元,激活函数为relu函数。
layers.Dense(100, activation='relu'),
# 第二隐含层,形式同上
layers.Dense(100, activation='relu'),
# 输出层,10个神经元,无激活函数
layers.Dense(10)
# Dense实现了以下操作:输出=激活(点(输入,内核)+偏置),其中激活是作为激活参数传递的元素激活函数,
# 内核是由层创建的权重矩阵,偏置是由层生成的偏置向量(仅当use_bias为True时适用)。这些都是“密集”的属性。
])
# 实现Adam算法的优化器。Adam优化是一种基于一阶和二阶矩自适应估计的随机梯度下降方法
optimizer = optimizers.Adam(0.0001) # 学习率设置为0.0001
# 配置用于训练的模型
model.compile(optimizer=optimizer, # 优化器实例
loss='sparse_categorical_crossentropy', # 指定损失函数为交叉熵损失函数
metrics=['accuracy'], # 指定模型评估度量指标为accuracy(精确度)
)
train_ds, test_ds = mnist_dataset() # 得到训练集和测试集
# Trains the model for a fixed number of epochs (iterations on a dataset).
model.fit(train_ds, epochs=5) # 指定模型迭代次数为5次
x = model.evaluate(test_ds) # 返回测试模式下模型的损失值和度量值
print("loss value: ", x[0])
print("metrics: ", x[1])
tutorial_minst_fnn-tf2.0.py:使用TensorFlow的基础功能实现前馈神经网络
# -*- coding: utf-8 -*-
# @Author : Xenon
# @Date : 2022/12/3 23:57
# @IDE : PyCharm(2022.2.3) Python3.9.13
"""使用TensorFlow的基础功能实现前馈神经网络"""
import os
import tensorflow as tf
from keras.datasets import mnist
from keras.api.keras import optimizers
# from tensorflow.keras import layers, optimizers, datasets
# 设置log信息等级 INFO(通知0)
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
def mnist_dataset():
"""读取TensorFlow自带的mnist手写字体数据集。
:return:训练集ds, 测试集test_ds(使用TensorFlow的dataset形式)
"""
# 从训练集提取20000个数据(共60000个)
(x, y), (x_test, y_test) = mnist.load_data() # 加载MNIST数据集。
# 创建一个数据集,其元素是给定张量的切片。切片2维张量生成1维张量元素。
ds = tf.data.Dataset.from_tensor_slices((x, y))
# 将数据打乱顺序并分成200个batch,每个batch有100个样本。
ds = ds.map(prepare_mnist_features_and_labels) # 将map_func映射到此数据集的元素
ds = ds.take(20000).shuffle(20000).batch(100) # 装载20000个数据集打乱后分为100批
# 从测试集提取全部20000个数据,prepare_mnist_features_and_labels,打乱顺序,设置为1个batch
test_ds = tf.data.Dataset.from_tensor_slices((x_test, y_test))
test_ds = test_ds.map(prepare_mnist_features_and_labels)
test_ds = test_ds.take(20000).shuffle(20000).batch(20000)
return ds, test_ds
def prepare_mnist_features_and_labels(x, y):
"""
将x转化成TensorFlow的32位浮点数(tf.float32),并除以255.0,
将y转化成TensorFlow的64位整数(tf.int64)
:param x: 原始张量x
:param y: 原始张量y
:return: x,y (dtype新类型)
"""
# 将张量强制转换为dtype新类型
x = tf.cast(x, tf.float32) / 255.0
y = tf.cast(y, tf.int64)
return x, y
class MyModel:
"""自定义模型类"""
def __init__(self):
# tf.Variable类型数据,形状为[28*28, 100],数据类型为tf.float32,初始值为-0.1到0.1的随机数,初始值形状与W1本身形状相同。
self.W1 = tf.Variable(shape=[28 * 28, 100], dtype=tf.float32,
initial_value=tf.random.uniform(shape=[28 * 28, 100],
minval=-0.1, maxval=0.1))
# tf.Variable类型数据,形状为[100],数据类型为tf.float32,初始值为0,初始值形状与b1本身形状相同。
self.b1 = tf.Variable(shape=[100], dtype=tf.float32, initial_value=tf.zeros(100))
# 以上属性说明,第一隐含层有100个神经元,上一层(第0层,输入层)有28*28=784个神经元
# tf.Variable类型数据,形状为[100, 10],数据类型为tf.float32,初始值为-0.1到0.1的随机数,初始值形状与W2本身形状相同。
self.W2 = tf.Variable(shape=[100, 10], dtype=tf.float32,
initial_value=tf.random.uniform(shape=[100, 10],
minval=-0.1, maxval=0.1))
# tf.Variable类型数据,形状为[10],数据类型为tf.float32,初始值为0,初始值形状与b2本身形状相同。
self.b2 = tf.Variable(shape=[10], dtype=tf.float32, initial_value=tf.zeros(10))
# 以上属性说明,输出层有10个神经元,上一层(第一隐含层)有100个神经元
# 由self.W1, self.W2, self.b1, self.b2构成的列表
self.trainable_variables = [self.W1, self.W2, self.b1, self.b2]
def __call__(self, x):
"""将输入的属性集中每一个二维样本转化为一维
注意,输入的是所有二维样本,因此共有三维,转化成相同数量的一维样本,因此转化之后共有二维)。
:param x: 输入的属性集
:return: 相同数量的一维样本
"""
flat_x = tf.reshape(x, shape=[-1, 28 * 28])
# 将结果其与W1矩阵相乘,加上偏置b1,然后用tanh激活函数处理。
# (注意,此时的输入值相当于转置的X,因此是X乘以W1,而非相反)
h1 = tf.tanh(tf.matmul(flat_x, self.W1) + self.b1)
# 将结果其与W2矩阵相乘,加上偏置b2,不用激活函数处理。
logists = tf.matmul(h1, self.W2) + self.b2
return logists
@tf.function
def compute_loss(logits, labels):
"""计算交叉熵损失函数
使用TensorFlow中的交叉熵损失函数,规定样本预测标签为logits形式,需要用softmax函数处理,真实标签未经独热向量处理,需要自动处理。然后返回平均损失。
:param logits:Logits形式的预测标签logits
:param labels:经独热向量处理的真实标签labels
:return:平均损失loss
"""
return tf.reduce_mean(
# 计算逻辑和标签之间的稀疏软最大交叉熵
tf.nn.sparse_softmax_cross_entropy_with_logits(logits=logits, labels=labels)
)
@tf.function
def compute_accuracy(logits, labels):
"""计算准确性
鉴于样本的标签是0-9,与数组下标相同,利用这一点进行判断。
:param logits: Logits形式的预测标签logits
:param labels: 未经独热向量处理的真实标签labels
:return: 准确率
"""
# 对预测标签logits使用tf.argmax函数(注意维度为1),得到预测结果predictions
predictions = tf.argmax(logits, axis=1)
# 使用tf.equal函数判断预测标签与真实标签是否相同,再计算准确率。
return tf.reduce_mean(tf.cast(tf.equal(predictions, labels), tf.float32))
@tf.function
def train_one_step(model, optimizer, x, y):
""" 进行训练(一个时间步)
:param model:模型model
:param optimizer:优化器optimizer(用于指定优化方法)
:param x:属性集x
:param y:真实标签集y
:return:损失loss, 准确性accuracy
"""
# 在梯度带中,调用模型的__call__方法
with tf.GradientTape() as tape:
logists = model(x)
loss = compute_loss(logists, y)
# 预测样本的标签,并调用compute_loss函数计算损失值。
grads = tape.gradient(loss, model.trainable_variables)
# 利用梯度带进行一次随机梯度下降法训练。
optimizer.apply_gradients(zip(grads, model.trainable_variables))
# 调用compute_accuracy函数计算准确性。
accuracy = compute_accuracy(logists, y)
return loss, accuracy
@tf.function
def _test_step(model, x, y):
"""执行预测
调用模型的__call__方法,预测样本的标签。
:param model:模型model
:param x:属性集x
:param y:真实标签集y
:return:损失loss, 准确性accuracy
"""
logists = model(x)
# 调用compute_loss函数计算损失值。
loss = compute_loss(logists, y)
# 调用compute_accuracy函数计算准确性。
accuracy = compute_accuracy(logists, y)
return loss, accuracy
def train(epoch, model, optimizer, ds):
"""进行训练(所有时间步)
:param epoch:轮数epoch
:param model:模型model
:param optimizer:优化器optimizer
:param ds:数据集ds
:return:损失loss, 准确性accuracy
"""
loss = 0.0
accuracy = 0.0
# 遍历数据集(TensorFlow的dataset形式)中的样本,调用train_one_step函数进行训练,
for step, (x, y) in enumerate(ds):
loss, accuracy = train_one_step(model, optimizer, x, y)
# 每次取出一个batch,在最后一个batch结束后,输出此刻的epoch, loss, accuracy。
print('epoch', epoch, ': loss', loss.numpy(), '; accuracy', accuracy.numpy())
return loss, accuracy
def my_test(model, ds):
"""进行测试
:param model:模型model
:param ds:数据集ds
:return:损失loss, 准确性accuracy
"""
loss = 0.0
accuracy = 0.0
# 遍历数据集(TensorFlow的dataset形式)中的样本,调用test_step函数进行测试,每次取出一个batch,
for step, (x, y) in enumerate(ds):
loss, accuracy = _test_step(model, x, y)
# 在最后一个batch结束后,输出此刻的loss, accuracy。(注:本实验中,测试集只有一个batch)
print('' , loss.numpy(), '; ' , accuracy.numpy())
return loss, accuracy
if __name__ == '__main__':
print("start")
model = MyModel() # 实列化自定义模型
optimizer = optimizers.Adam() # 实现Adam算法的优化器
# 调用函数mnist_dataset(),获取数据集train_ds, test_ds。
train_ds, test_ds = mnist_dataset()
# 在5轮中,利用train函数进行训练。
for epoch in range(5):
loss, accuracy = train(epoch, model, optimizer, train_ds)
# 利用test函数进行测试。
loss, accuracy = my_test(model, test_ds)
print("real损失loss: %f ; real准确性accuracy: %f" % (loss.numpy(), accuracy.numpy()))
SVM_sklearn.py:使用sk-learn实现支持向量机
# -*- coding: utf-8 -*-
# @Author : Xenon
# @Date : 2022/12/3 23:57
# @IDE : PyCharm(2022.2.3) Python3.9.13
"""使用sk-learn实现支持向量机,并完成手写数字识别任务。"""
import numpy as np
# import operator
from os import listdir
from sklearn.svm import SVC
def img2vector(filename):
"""将一张图片转化为一维向量
:param filename:文件名filename
:return:转换后的向量returnVect
"""
# 创建全0的numpy数组,形状为(1,1024)
returnVect = np.zeros((1, 1024))
fr = open(filename) # 读取文件
# 将第i行j列的像素赋值给numpy数组的32*i+j个元素,将所有像素进行赋值。
for i in range(32):
lineStr = fr.readline()
for j in range(32):
returnVect[0, 32 * i + j] = int(lineStr[j])
return returnVect
def run():
hwLabels = [] # 存储测试集的Labels
trainingDigits_path = "E:/wynuJunior/模式识别/6前馈神经网络与支持向量机/新建文件夹/trainingDigits"
testDigits_path = "E:/wynuJunior/模式识别/6前馈神经网络与支持向量机/新建文件夹/testDigits"
trainingFileList = listdir(trainingDigits_path) # 使用listdir返回trainingDigits目录下的文件名
if '.ipynb_checkpoints' in trainingFileList:
trainingFileList.remove('.ipynb_checkpoints')
m = len(trainingFileList) # 返回文件夹下文件的个数
# 初始化训练的trainingMat矩阵为(m, 1024)形状的全零numpy数组,
trainingMat = np.zeros((m, 1024))
# 依次读取trainingDigits目录下的文件
for i in range(m):
fileNameStr = trainingFileList[i]
classNumber = int(fileNameStr.split('_')[0]) # 将文件名中下划线“_”前面的字符作为类别
hwLabels.append(classNumber)
# 使用img2vector函数读取属性并转化为一维向量.分别存储在hwLabels与trainingMat矩阵中
trainingMat[i, :] = img2vector(trainingDigits_path + "/" + fileNameStr)
# 将SVC模型实例化,松弛向量超参数C为200,核函数为rbf
clf = SVC(C=200, kernel='rbf')
# 调用fit方法,输入trainingMat与hwLabels
clf.fit(trainingMat, hwLabels)
testFileList = listdir(testDigits_path)
if '.ipynb_checkpoints' in trainingFileList:
trainingFileList.remove('.ipynb_checkpoints')
errorCount = 0.0
mTest = len(testFileList)
# 使用相同的方法读取测试数据,测试数据存储在文件夹testDigits中,每读取一个数据,
# 调用SVC模型的predict方法进行预测,输出分类返回结果,真实结果,并统计错误次数,最终输出错误率。
for i in range(mTest):
fileNameStr = testFileList[i]
classNumber = int(fileNameStr.split('_')[0])
vectorUnderTest = img2vector(testDigits_path + "/" + fileNameStr)
classifierResult = clf.predict(vectorUnderTest)
print("分类返回结果为%d\t真实结果为%d" % (classifierResult, classNumber))
if classifierResult != classNumber:
errorCount += 1.0
print("总共错了%d个数据\n错误率为%f%%" % (errorCount, errorCount / mTest * 100))
if __name__ == '__main__':
run()
tutorial_minst_fnn-numpy.py:手写实现前馈神经网络(仅使用numpy,包括手写反向传播算法求解过程)
# -*- coding: utf-8 -*-
# @Author : Xenon
# @Date : 2022/12/3 23:58
# @IDE : PyCharm(2022.2.3) Python3.9.13
"""手写实现前馈神经网络(仅允许使用numpy,需要手写反向传播算法求解过程)
神经网络与深度学习(邱锡鹏)编程练习4 FNN 简单神经网络 Jupyter导出版 numpy """
import os
import numpy as np
from keras.datasets import mnist
import tensorflow as tf
# 设置log信息等级 INFO(通知0)
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
# =============== 准备数据 ===============
def mnist_dataset():
"""读取mnist手写字体数据集。
:return:训练集(x, y), 测试集(x_test, y_test)
"""
(x, y), (x_test, y_test) = mnist.load_data()
x = x / 255.0
x_test = x_test / 255.0
return (x, y), (x_test, y_test)
# ===============Demo numpy based auto differentiation===============
class Matmul:
def __init__(self):
self.mem = {}
def forward(self, x, W):
"""前向传播"""
h = np.matmul(x, W)
self.mem = {'x': x, 'W': W}
return h
def backward(self, grad_y):
"""反向传播
x: shape(N, d)
w: shape(d, d')
grad_y: shape(N, d')
"""
x = self.mem['x']
W = self.mem['W']
grad_x = np.matmul(grad_y, W.T) # shape(N, b)
grad_W = np.matmul(x.T, grad_y)
return grad_x, grad_W
class Relu:
def __init__(self):
self.mem = {}
def forward(self, x):
"""前向传播"""
self.mem['x'] = x
return np.where(x > 0, x, np.zeros_like(x))
def backward(self, grad_y):
"""反向传播
grad_y: same shape as x
"""
x = self.mem['x']
return (x > 0).astype(np.float32) * grad_y
class Softmax:
"""
softmax over last dimention
"""
def __init__(self):
self.epsilon = 1e-12
self.mem = {}
def forward(self, x):
"""前向传播
x: shape(N, c)
"""
x_exp = np.exp(x)
partition = np.sum(x_exp, axis=1, keepdims=True)
out = x_exp / (partition + self.epsilon)
self.mem['out'] = out
self.mem['x_exp'] = x_exp
return out
def backward(self, grad_y):
"""反向传播
grad_y: same shape as x
"""
s = self.mem['out']
sisj = np.matmul(np.expand_dims(s, axis=2), np.expand_dims(s, axis=1)) # (N, c, c)
g_y_exp = np.expand_dims(grad_y, axis=1)
tmp = np.matmul(g_y_exp, sisj) # (N, 1, c)
tmp = np.squeeze(tmp, axis=1)
tmp = -tmp + grad_y * s
return tmp
class Log:
"""
softmax over last dimention
"""
def __init__(self):
self.epsilon = 1e-12
self.mem = {}
def forward(self, x):
"""前向传播
x: shape(N, c)
"""
out = np.log(x + self.epsilon)
self.mem['x'] = x
return out
def backward(self, grad_y):
"""反向传播
grad_y: same shape as x
"""
x = self.mem['x']
return 1. / (x + 1e-12) * grad_y
# ===============Gradient check===============
def Gradient_check():
x = np.random.normal(size=[5, 6])
W1 = np.random.normal(size=[6, 5])
W2 = np.random.normal(size=[5, 6])
label = np.zeros_like(x)
label[0, 1] = 1.
label[1, 0] = 1
label[2, 3] = 1
label[3, 5] = 1
label[4, 0] = 1
mul_h1 = Matmul()
mul_h2 = Matmul()
relu = Relu()
softmax = Softmax()
log = Log()
h1 = mul_h1.forward(x, W1) # shape(5, 4)
h1_relu = relu.forward(h1)
h2 = mul_h2.forward(h1_relu, W2)
h2_soft = softmax.forward(h2)
h2_log = log.forward(h2_soft)
h2_log_grad = log.backward(label)
h2_soft_grad = softmax.backward(h2_log_grad)
h2_grad, W2_grad = mul_h2.backward(h2_soft_grad)
h1_relu_grad = relu.backward(h2_grad)
h1_grad, W1_grad = mul_h1.backward(h1_relu_grad)
print(h2_log_grad)
print('--' * 20)
# print(W2_grad)
with tf.GradientTape() as tape:
x, W1, W2, label = tf.constant(x), tf.constant(W1), tf.constant(W2), tf.constant(label)
tape.watch(W1)
tape.watch(W2)
h1 = tf.matmul(x, W1)
h1_relu = tf.nn.relu(h1)
h2 = tf.matmul(h1_relu, W2)
prob = tf.nn.softmax(h2)
log_prob = tf.math.log(prob)
loss = tf.reduce_sum(label * log_prob)
grads = tape.gradient(loss, [prob])
print(grads[0].numpy())
# ===============建立模型===============
class MyModel:
def __init__(self):
self.W1 = np.random.normal(size=[28 * 28 + 1, 100])
self.W2 = np.random.normal(size=[100, 10])
self.mul_h1 = Matmul()
self.mul_h2 = Matmul()
self.relu = Relu()
self.softmax = Softmax()
self.log = Log()
def forward(self, x):
x = x.reshape(-1, 28 * 28)
bias = np.ones(shape=[x.shape[0], 1])
x = np.concatenate([x, bias], axis=1)
self.h1 = self.mul_h1.forward(x, self.W1) # shape(5, 4)
self.h1_relu = self.relu.forward(self.h1)
self.h2 = self.mul_h2.forward(self.h1_relu, self.W2)
self.h2_soft = self.softmax.forward(self.h2)
self.h2_log = self.log.forward(self.h2_soft)
def backward(self, label):
self.h2_log_grad = self.log.backward(-label)
self.h2_soft_grad = self.softmax.backward(self.h2_log_grad)
self.h2_grad, self.W2_grad = self.mul_h2.backward(self.h2_soft_grad)
self.h1_relu_grad = self.relu.backward(self.h2_grad)
self.h1_grad, self.W1_grad = self.mul_h1.backward(self.h1_relu_grad)
# ===============计算 loss===============
def compute_loss(log_prob, labels):
"""计算交叉熵损失函数
使用TensorFlow中的交叉熵损失函数,规定样本预测标签为logits形式,需要用softmax函数处理,真实标签未经独热向量处理,需要自动处理。然后返回平均损失。
:param log_prob:Logits形式的预测标签logits
:param labels:经独热向量处理的真实标签labels
:return:平均损失loss
"""
return np.mean(np.sum(-log_prob * labels, axis=1))
def compute_accuracy(log_prob, labels):
"""计算精确度
鉴于样本的标签是0-9,与数组下标相同,利用这一点进行判断。
:param log_prob: Logits形式的预测标签
:param labels: 未经独热向量处理的真实标签labels
:return: 准确率
"""
predictions = np.argmax(log_prob, axis=1)
truth = np.argmax(labels, axis=1)
return np.mean(predictions == truth)
def train_one_step(model, x, y):
"""进行训练(一个时间步)"""
model.forward(x)
model.backward(y)
model.W1 -= 1e-5 * model.W1_grad
model.W2 -= 1e-5 * model.W2_grad
loss = compute_loss(model.h2_log, y)
accuracy = compute_accuracy(model.h2_log, y)
return loss, accuracy
def _test(model, x, y):
"""执行预测"""
model.forward(x)
loss = compute_loss(model.h2_log, y)
accuracy = compute_accuracy(model.h2_log, y)
return loss, accuracy
# ===============实际训练===============
def train():
model = MyModel()
train_data, test_data = mnist_dataset()
train_label = np.zeros(shape=[train_data[0].shape[0], 10])
test_label = np.zeros(shape=[test_data[0].shape[0], 10])
train_label[np.arange(train_data[0].shape[0]), np.array(train_data[1])] = 1.
test_label[np.arange(test_data[0].shape[0]), np.array(test_data[1])] = 1.
for epoch in range(50):
loss, accuracy = train_one_step(model, train_data[0], train_label)
print('epoch', epoch, ': loss', loss, '; accuracy', accuracy)
loss, accuracy = _test(model, test_data[0], test_label)
print('test loss', loss, '; accuracy', accuracy)
if __name__ == '__main__':
print(">>>>>>>>>>Final Gradient Check:")
Gradient_check()
print("\n>>>>>>>>>>>>>实际训练:")
train()
SVM_manual.py:手写支持向量机(包括支持向量机的优化算法——SMO算法)
# -*- coding: utf-8 -*-
# @Author : Xenon
# @Date : 2022/12/3 23:59
# @IDE : PyCharm(2022.2.3) Python3.9.13
"""手写支持向量机(包括支持向量机的优化算法——SMO算法)"""
import numpy as np
np.random.seed(1) # 设置初始随机数种子
class SVC:
def __init__(self, max_iter=100, C=1, kernel='rbf', sigma=1):
self.b = 0.
self.alpha = None
self.max_iter = max_iter
self.C = C
self.kernel = kernel
self.K = None
self.X = None
self.y = None
if kernel == 'rbf':
self.sigma = sigma
def kernel_func(self, kernel, x1, x2):
if kernel == 'linear':
return x1.dot(x2.T)
elif kernel == 'rbf':
return np.exp(-(np.sum((x1 - x2) ** 2)) / (2 * self.sigma * self.sigma))
def computeK(self, X, kernel):
m = X.shape[0]
K = np.zeros((m, m))
for i in range(m):
for j in range(m):
if i <= j:
K[i, j] = self.kernel_func(kernel, X[i], X[j])
else:
K[i, j] = K[j, i]
return K
def compute_u(self, X, y):
u = np.zeros((X.shape[0],))
for j in range(X.shape[0]):
u[j] = np.sum(y * self.alpha * self.K[:, j]) + self.b
return u
def checkKKT(self, u, y, i):
if self.alpha[i] < self.C and y[i] * u[i] <= 1:
return False
if self.alpha[i] > 0 and y[i] * u[i] >= 1:
return False
if (self.alpha[i] == 0 or self.alpha[i] == self.C) and y[i] * u[i] == 1:
return False
return True
def fit(self, X, y):
self.X = X
self.y = y
self.K = self.computeK(X, self.kernel)
self.alpha = np.random.random((X.shape[0],))
self.omiga = np.zeros((X.shape[0],))
for _ in range(self.max_iter):
u = self.compute_u(X, y)
finish = True
for i in range(X.shape[0]):
if not self.checkKKT(u, y, i):
finish = False
y_indices = np.delete(np.arange(X.shape[0]), i)
j = y_indices[int(np.random.random() * len(y_indices))]
E_i = np.sum(self.alpha * y * self.K[:, i]) + self.b - y[i]
E_j = np.sum(self.alpha * y * self.K[:, j]) + self.b - y[j]
if y[i] != y[j]:
L = max(0, self.alpha[j] - self.alpha[i])
H = min(self.C, self.C + self.alpha[j] - self.alpha[i])
else:
L = max(0, self.alpha[j] + self.alpha[i] - self.C)
H = min(self.C, self.alpha[j] + self.alpha[i])
eta = self.K[i, i] + self.K[j, j] - 2 * self.K[i, j]
alpha2_new_unc = self.alpha[j] + y[j] * (E_i - E_j) / eta
alpha2_old = self.alpha[j]
alpha1_old = self.alpha[i]
if alpha2_new_unc > H:
self.alpha[j] = H
elif alpha2_new_unc < L:
self.alpha[j] = L
else:
self.alpha[j] = alpha2_new_unc
self.alpha[i] = alpha1_old + y[i] * y[j] * (alpha2_old - self.alpha[j])
b1_new = -E_i - y[i] * self.K[i, i] * (self.alpha[i] - alpha1_old) - y[j] * self.K[j, i] * (
self.alpha[j] - alpha2_old) + self.b
b2_new = -E_j - y[i] * self.K[i, j] * (self.alpha[i] - alpha1_old) - y[j] * self.K[j, j] * (
self.alpha[j] - alpha2_old) + self.b
if 0 < self.alpha[i] < self.C:
self.b = b1_new
elif 0 < self.alpha[j] < self.C:
self.b = b2_new
else:
self.b = (b1_new + b2_new) / 2
if finish:
break
def predict(self, X):
y_preds = []
for i in range(X.shape[0]):
K = np.zeros((len(self.y),))
support_indices = np.where(self.alpha > 0)[0]
for j in support_indices:
K[j] = self.kernel_func(self.kernel, self.X[j], X[i])
y_pred = np.sum(self.y[support_indices] * self.alpha[support_indices] * K[support_indices].T)
y_pred += self.b
y_preds.append(y_pred)
return np.array(y_preds)
def rbf_test():
"""# 测试rbf核"""
X = np.array([[1, 0], [-1, 0], [0, -1], [0, 1], [2, np.sqrt(5)],
[2, -np.sqrt(5)], [-2, np.sqrt(5)], [-2, -np.sqrt(5)],
[300, 400]])
y = np.array([-1, -1, -1, -1, 1, 1, 1, 1, 1])
svc = SVC(max_iter=100, kernel='rbf', C=1)
if __name__ == '__main__':
# 测试 线性核
X = np.array([[2, -1], [3, -2], [1, 0], [0, 1], [-2, 1], [-1.3, 0.3], [-0.2, -0.8], [2.3, -3.3], [-2, -4], [7, 8]])
y = np.array([1, 1, 1, 1, -1, -1, -1, -1, -1, 1])
svc = SVC(max_iter=100, kernel='linear', C=1)
# rbf_test() # 测试rbf核
svc.fit(X, y)
print('alpha:', svc.alpha)
print('b:', svc.b)
pred_y = svc.predict(np.array([[1, 0], [-0.2, -0.1], [0, 1]]))
print('pred_y1:', pred_y)
pred_y = np.sign(pred_y)
print('pred_y:', pred_y)
七、实验结果分析
tutorial_minst_fnn-keras.py:使用TensorFlow的Sequential实现的前馈神经网络
tutorial_minst_fnn-tf2.0.py:使用TensorFlow的基础功能实现前馈神经网络
SVM_sklearn.py:使用sk-learn实现的支持向量机
tutorial_minst_fnn-numpy.py:手写实现前馈神经网络
>>>>>>>>>>Final Gradient Check:
[[ 0. 13.56517147 0. 0. 0.
0. ]
[ 9.13109205 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 28.76783616 0.
0. ]
[ 0. 0. 0. 0. 0.
2.08812302]
[223.30349106 0. 0. 0. 0.
0. ]]
----------------------------------------
[[ 0. 13.56517147 0. 0. 0.
0. ]
[ 9.13109205 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 28.76783616 0.
0. ]
[ 0. 0. 0. 0. 0.
2.08812302]
[223.30349111 0. 0. 0. 0.
0. ]]
>>>>>>>>>>>>>实际训练:
epoch 0 : loss 22.744282639414152 ; accuracy 0.14281666666666668
epoch 1 : loss 21.758409494243114 ; accuracy 0.19443333333333335
epoch 2 : loss 21.055453298219938 ; accuracy 0.21456666666666666
epoch 3 : loss 19.97412670942362 ; accuracy 0.2425
epoch 4 : loss 19.331889706730408 ; accuracy 0.27365
epoch 5 : loss 18.67261661508262 ; accuracy 0.28918333333333335
epoch 6 : loss 18.05297102157659 ; accuracy 0.3132666666666667
epoch 7 : loss 17.391424059042368 ; accuracy 0.3335666666666667
epoch 8 : loss 16.92636561898056 ; accuracy 0.3537
epoch 9 : loss 16.468125340459746 ; accuracy 0.36415
epoch 10 : loss 16.029440126389247 ; accuracy 0.38426666666666665
epoch 11 : loss 15.124473109925919 ; accuracy 0.4094
epoch 12 : loss 14.933236383252314 ; accuracy 0.42401666666666665
epoch 13 : loss 14.077481388808991 ; accuracy 0.4544
epoch 14 : loss 13.822439579397273 ; accuracy 0.46923333333333334
epoch 15 : loss 13.569737829512812 ; accuracy 0.4776666666666667
epoch 16 : loss 13.408817890037813 ; accuracy 0.48535
epoch 17 : loss 13.251820335335175 ; accuracy 0.49325
epoch 18 : loss 13.131440207863612 ; accuracy 0.4978666666666667
epoch 19 : loss 13.030534873523466 ; accuracy 0.50235
epoch 20 : loss 12.941951598415892 ; accuracy 0.50645
epoch 21 : loss 12.864857315106821 ; accuracy 0.5098166666666667
epoch 22 : loss 12.795055337736255 ; accuracy 0.5131
epoch 23 : loss 12.731265095920785 ; accuracy 0.5157333333333334
epoch 24 : loss 12.672742610871332 ; accuracy 0.5183166666666666
epoch 25 : loss 12.619165846144682 ; accuracy 0.521
epoch 26 : loss 12.570194346481664 ; accuracy 0.5236333333333333
epoch 27 : loss 12.525412347113768 ; accuracy 0.5256166666666666
epoch 28 : loss 12.484171010564536 ; accuracy 0.5274666666666666
epoch 29 : loss 12.445748592079973 ; accuracy 0.5291166666666667
epoch 30 : loss 12.409322682637926 ; accuracy 0.5306666666666666
epoch 31 : loss 12.375371239003229 ; accuracy 0.5323
epoch 32 : loss 12.343667769125867 ; accuracy 0.5334666666666666
epoch 33 : loss 12.313774902029765 ; accuracy 0.5348
epoch 34 : loss 12.285461088940856 ; accuracy 0.5360833333333334
epoch 35 : loss 12.258628543611174 ; accuracy 0.5373833333333333
epoch 36 : loss 12.233472765057796 ; accuracy 0.53875
epoch 37 : loss 12.20993121146134 ; accuracy 0.5399666666666667
epoch 38 : loss 12.187759138875334 ; accuracy 0.5408833333333334
epoch 39 : loss 12.166864181880165 ; accuracy 0.5418
epoch 40 : loss 12.147133028128476 ; accuracy 0.5427833333333333
epoch 41 : loss 12.128473068549651 ; accuracy 0.5436333333333333
epoch 42 : loss 12.11088791201951 ; accuracy 0.54475
epoch 43 : loss 12.094389768803017 ; accuracy 0.5456666666666666
epoch 44 : loss 12.078837652166147 ; accuracy 0.54635
epoch 45 : loss 12.063933847899557 ; accuracy 0.5471333333333334
epoch 46 : loss 12.04946994696933 ; accuracy 0.5477
epoch 47 : loss 12.035382923777563 ; accuracy 0.5485166666666667
epoch 48 : loss 12.021645774882836 ; accuracy 0.54925
epoch 49 : loss 12.00810636704182 ; accuracy 0.5498666666666666
test loss 12.11529551663803 ; accuracy 0.5449
SVM_manual.py:手写实现支持向量机