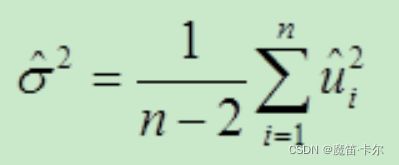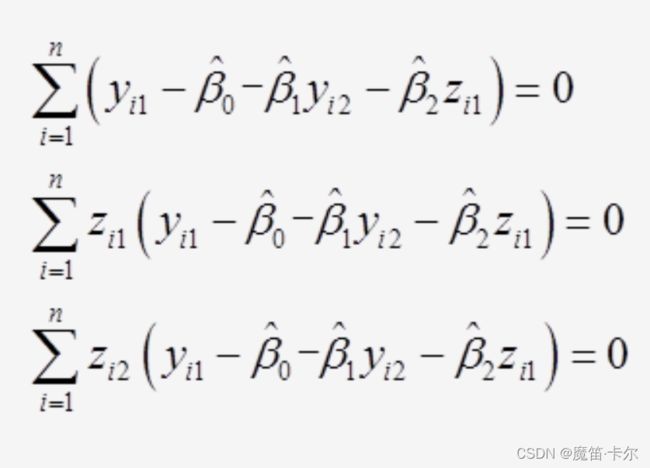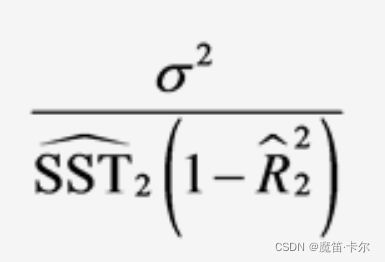工具变量估计与两阶段最小二乘法

1. 简单模型的工具变量法

假设一个简单回归模型为y＝β0＋β1x＋u，其中x与u相关：Cov（x，u）≠0。

（1）为了在x和u相关时得到β0和β1的一致估计量，需要有一个可观测到的变量z，z满足两个假定：

①工具外生性条件，z与u不相关，即Cov（z，u）＝0，意味着z应当对y无偏效应（一旦x和u中的遗漏变量被控制），也不应当与其他影响y的无法观测因素相关；

②工具相关性条件，z与x相关，即Cov（z，x）≠0，意味着z应当与内生解释变量x相关。

满足这两个条件的z被称为x的工具变量（IV），简称为x的工具。

（2）工具变量的两个要求之间的差别：

①由于通常无法检验z与无法观测误差u的协方差，一般通过经济行为或反思来维持这一假定。

②可以检验z与内生解释变量x的相关性。

最容易的方法是在总体中估计x与z之间的回归：x＝π0＋π1z＋v，由于

π1＝Cov（z，x）/Var（z）

所以当且仅当π1≠0时式Cov（z，x）≠0成立。若能在充分小的显著水平上，相对双侧对立假设H1：π1≠0而拒绝虚拟假设H0：π1＝0，则有把握证明工具z与x是相关的。

但需要注意π1的符号，因为有时负向相关关系难以证明工具变量的合理性。

2. 工具变量估计量

（1）参数的工具变量（IV）估计量

首先说明如何使用工具变量的假定来识别β1并得出β1的表达式。利用简单回归方程可得z与y之间的协方差为：

Cov（z，y）＝β1Cov（z，x）＋Cov（z，u）

在Cov（z，u）＝0与Cov（z，x）≠0的假定下，可以解出β1为：

β1＝Cov（z，y）/Cov（z，x）

因为能够利用总体协方差写出β1，所以β1被识别了。假设总体中的一个随机样本，在分子和分母中约去样本容量后，得到β1的工具变量（IV）估计量：

β0的IV估计量为：β∧0＝y＿－β∧1x＿。

（2）工具变量估计量的一致性和无偏性

大数定律表明，若满足工具变量的两个假定，β1的IV估计量便具有一致性：

plim（β∧1）＝β1

工具变量的两个假定是IV估计量具有一致性的必要条件。

但当x与u相关时，IV估计量是有偏误的，尤其是在小样本中偏误有可能很大。因此在使用工具变量法时，需要大的样本容量。

3. 用IV估计量做统计推断

（1）β1的渐进方差

在大样本容量的情况下，IV估计量近似服从正态分布。此时需要假设同方差，即E（u2|z）＝σ2＝Var（u）。

在同方差假定和IV假定下，β∧1的渐近方差为：σ2/（nσx2ρx，z2）。其中，σx2是x的总体方差，σ2是u的总体方差，ρx，z2是x与z的总体相关系数的平方，它反映了总体中z与x的相关性有多大。

（2）渐进方差的意义

①提供了一种求IV估计量标准误的方法。

给定一个随机样本，可以一致地估计渐进误差中的所有量。为估计σx2，可以计算xi的样本方差；为估计ρx，z2，可以进行xi对zi的回归得到R2，即Rx，z2。最后，为估计σ2，可以利用IV残差，u∧i＝yi－β∧0－β∧1xi，i＝1，2，…，n。其中，β∧0与β∧1是IV估计量。σ2的一致估计量为：

β∧1的渐近标准误是所估计的渐进方差的平方根，这个方差为：σ∧2/（SSTx·Rx，z2）。

其中，SSTx是xi的总平方和，SSTx/n是xi的样本方差。利用渐进标准误可以构造t统计量来检验关于β1的假设。

②比较x与u不相关情况下OLS估计量和IV的渐近方差。

在高斯-马尔可夫假定下，OLS估计量的方差为σ2/SSTx，而IV估计量的计算式为σ2/（SSTx·Rx，z2）；由于Rx，z2总是小于1，所以IV方差总是大于OLS方差。

当z＝x时，Rx，z2＝1，得到OLS的方差。z与x相关程度越高，Rx，z2便越接近于1，IV估计量的方差就越小。若x与z轻度相关，Rx，z2便很小，IV估计量的抽样方差就将非常大。

当x与u不相关时，进行IV估计会导致IV估计量的渐近方差总是大于（有时远大于）OLS估计量的渐近方差。

4. 低劣工具变量条件下IV的性质（见表15-1）

表15-1　低劣工具变量条件下IV的性质

5. IV估计后计算R2

IV估计之后的R2标准公式：

R2＝1－SSR/SST

其中SSR是IV残差的平方和，SST是y的总平方和。

与OLS不同，由于IV估计中的SSR可能大于SST，所以其R2可能为负。不过IV估计主要用于解决系数的不一致问题，拟合优度不是特别重要。

6. 多元回归模型的IV估计

6.1 结构方程

两个解释变量条件下的标准线性模型：y1＝β0＋β1y2＋β2z1＋u1，由于该方程不一定表示某种因果关系，所以称之为结构方程。方程中，变量y2和z1是解释变量，u1是误差。假定u1的期望值为0：E（u1）＝0。因为y1与u1相关，因变量y1是内生变量；z1与u1不相关，z1是外生变量，用y2表示该变量被怀疑与u1相关。

6.2 工具变量法

方程y1＝β0＋β1y2＋β2z1＋u1的OLS估计量是有偏且不一致的，因此使用工具变量法。采用外生变量z2为工具变量，关键假定是z1和z2与u1不相关且u1具有零均值，即有E（u1）＝0，Cov（z1，u1）＝0和Cov（z2，u1）＝0，后两个假定等价于E（z1u1）＝E（z2u1）＝0，通过样本矩条件得到β∧0、β∧1和β∧2：

利用样本数据很容易求解以上方程组，得到β∧0、β∧1和β∧2的工具变量估计量。如果认为y2是外生的，并选择z2＝y2，该方程其实就是OLS估计量的一阶条件。

工具变量z2必须与y2相关，将内生解释变量写成关于外生变量和误差项的一个线性函数：

y2＝π0＋π1z1＋π2z2＋v2

其中根据构造有：

E（v2）＝0，Cov（z1，v2）＝0，Cov（z2，v2）＝0

其中，πj是未知参数。关键的识别条件是：π2≠0，即在排除了z1的影响后，y2与z2仍然相关，使用t检验就可以检验π2≠0，但是无法检验z1和z2与u1不相关。

6.3 更多外生解释变量的模型

添加更多的外生解释变量，结构模型为：

y1＝β0＋β1y2＋β2z1＋…＋βkzk－1＋u1

其中，y2与u1相关。令zk是上式中未包含的外生变量。

假定E（u1）＝0，Cov（zj，u1）＝0，j＝1，…，k；z1，…，zk－1是外生变量。

y2的约简型是：

y2＝π0＋π1z1＋…＋πk－1zk－1＋πkzk＋v2

zk与y2相关的假定可写成：

πk≠0

在满足上面两个假定的情况下，此时zk是y2的一个有效IV。此外，还需要假定外生变量之间不存在完全线性关系以及u1的同方差性。

7. 两阶段最小二乘　★★★★★

7.1 单个内生解释变量

假定z2和z3是两个被排斥在式y1＝β0＋β1y2＋β2z1＋u1之外的外生变量，且满足排除性约束：z2和z3不出现在上式中，且与误差项u1不相关。

（1）最好的IV

若z2和z3都与y2相关，可以选择任意一个作为IV，但通常得到的两个IV估计量都不是有效的。由于z1、z2和z3都与u1不相关，它们的任何线性组合也与u1不相关。因此，通过构建外生变量的线性组合可以寻找最有效的IV。选择与y2最高度相关的线性组合：

y2＝π0＋π1z1＋π2z2＋π3z3＋v2

其中，E（v2）＝0，Cov（z1，v2）＝0，Cov（z2，v2）＝0，Cov（z3，v2）＝0。

则y2最好的IV是y2*：y2*＝π0＋π1z1＋π2z2＋π3z3，为满足该IV与z1不完全相关的假定，需要π2≠0或π3≠0，可以用F统计量来检验。关键的识别假定是，zj全部是外生的。若π2＝0且π3≠0，结构方程式不能被识别。

（2）求解两阶段最小二乘（2SLS）估计量

首先用OLS估计约简型，将y2对z1、z2和z3回归，获得拟合值：

y∧2＝π∧0＋π∧1z1＋π∧2z2＋π∧3z3

此时，检验z2与z3的联合显著性；若z2与z3不是联合显著的，进行IV估计便是无意义的。一旦有了y∧2，便可以用它作为y2的IV。用y∧2代替y2重新进行OLS回归，重新估计原方程的系数。

在多重工具情况下，IV估计量也称为两阶段最小二乘（2SLS）估计量。

（3）2SLS具备理想的大样本性质所需要的假定

在结构方程为y1＝β0＋β1y2＋β2z1＋…＋βkzk－1＋u1中，需要假定：

①每个zj与u1都不相关。

②为了使估计量一致，至少需要一个与y2偏相关的外生变量不在上式之中。

③为了使通常的2SLS标准误和t统计量渐近有效，需要同方差假定：任何外生变量都不与结构误差u1的方差相关。

7.2 多重共线性与2SLS

（1）在2SLS条件下，多重共线性会造成更严重的偏差

β1的2SLS估计量的渐近方差可以近似地写为：

 

其中，σ2＝Var（u1），是y∧2中的总变异，R∧22是将y∧2对其他所有出现在结构方程中的外生变量做回归得到的R2。当R∧22接近于1，2SLS估计值的标准误将非常大，但在大样本条件下，该问题可以忽略。

（2）2SLS的方差大于OLS方差的原因

①y∧2比y2的变异更小。因为y∧2中变异构成第一阶段回归的解释平方和，而y2中的变异构成总平方和。

②与y2相比，y∧2与式y1＝β0＋β1y2＋β2z1＋…＋βkzk－1＋u1中外生变量之间的相关性更高，这就解释了2SLS中为什么存在多重共线性问题。

8. 变量误差问题的IV解决方法

用工具变量解决测量误差问题，对如下模型：

y＝β0＋β1x1*＋β2x2＋u

其中，y和x2是可观测的，x1*不可观测。令x1是x1*的一个可观测度量：x1＝x1*＋e1，其中e1是测量误差。x1与e1之间的相关性会导致OLS（其中用x1代替了x1*）的有偏和不一致性，即

y＝β0＋β1x1＋β2x2＋（u－β1e1）

如果满足经典的变量误差（CEV）假定，则β1的OLS估计量有向零偏误。

某些情况中，IV方法可以解决测量误差问题。假定模型中u与x1*、x1和x2不相关；在CEV条件下，假定e1与x1*和x2不相关。以上假定说明x2在上式中是外生的，只是x1与e1相关。因此，需要寻找x1的IV，满足：与x1相关但与误差项和测量误差e1不相关。

寻找IV的方法有：第一种方法是获取x1*的第二个度量，即z1。另一种方法是将其他外生变量作为潜在误测变量的IV。

9. 内生性检验与过度识别约束检验　★★★★★

9.1 内生性检验

（1）豪斯曼检验

若解释变量外生，2SLS估计量的偏误会很大，采用OLS将更有效。因此，在回归之前需要检验解释变量的内生性。

假定模型y1＝β0＋β1y2＋β2z1＋β3z2＋u1中y2可能是内生变量，且已知z1和z2是外生的。

若所有变量都是外生的，则OLS和2SLS都是一致的。因此，豪斯曼检验的做法是：直接比较OLS和2SLS估计值，判断其差异是否在统计上显著。若差异明显，则y2必定是内生的。

（2）回归检验

估计y2的约简型：y2＝π0＋π1z1＋π2z2＋π3z3＋π4z4＋v2，因为zj与u1不相关，所以y2与u1不相关的充分条件是v2与u1不相关，因此只需检验v2与u1不相关。利用u1＝δ1v2＋e1（其中e1与v2不相关，具有零均值）检验δ1＝0。具体做法是在原估计模型中添加v2，由于v2的不可观测性，可以用残差v∧2代替，再用OLS估计y1＝β0＋β1y2＋β2z1＋β3z2＋δ1v∧2＋u1，并用t统计量检验H0：δ1＝0。若能在很小的显著性水平下拒绝H0，则y2是内生的。

（3）检验单个解释变量的内生性

①估计y2的约简型方程，即做y2对所有外生变量（包括结构方程中的外生变量和额外的IV）的回归，并计算残差v∧2。

②将残差v∧2加入包含y2的结构方程并使用OLS估计，用异方差-稳健的t统计量检验v∧2。若v∧2的系数统计显著异于零，则y2是内生的。

第②部分回归的特点：除v∧2外，所有变量的估计值都与2SLS估计值相等。

9.2 检验过度识别约束

（1）过度识别约束

为了一致地估计参数，所拥有的工具数量多于需要的工具数量称为过度识别约束。

假设工具变量的数量比需要的数量多q个，就有过度识别约束，这时比较几个不同的IV估计值就比较困难，但可以借助2SLS残差计算检验统计量。若所有的工具都是外生的，则2SLS残差应该与除抽样误差外的工具不相关。若有k＋1个参数和k＋1＋q个工具，则2SLS残差的均值为0，且与这些工具的k个线性组合不相关。因此，需要检验2SLS残差与这些工具的q个线性组合的相关性。

（2）回归检验过度识别约束

①用2SLS估计结构方程，获得2SLS残差u∧1；

②将u∧1对所有外生变量回归，获得R2，即R12；

③若虚拟假设成立，所有IV都与u1不相关，则有，其中q是模型之外的工具变量数目减去内生解释变量的总数目。若nR12超过了χq2分布中的5%临界值，则拒绝H0，即至少部分IV不是外生的。

在满足标准2SLS假定的情况下，增添变量能够提高2SLS的渐近有效性，但这建立在任何一个新工具都是外生的条件下，否则2SLS将不一致。在具备适度的样本容量可供使用的条件下，增添过多的工具（即增加过度识别约束的数目）会导致2SLS出现严重偏误。

只要工具变量的数量比需要的数量多，都可以使用过度识别检验。若工具恰好足够，则该模型是恰好识别的，②中的R2将恒等于零，工具的外生性也无法检验。

10. 2SLS应用其他数据类型

10.1时间序列方程的应用

将2SLS应用在时间序列方程中与应用在横截面数据本质上没有差别，但是需要将误差项的序列相关考虑进来。实际的操作也是相同的，但是需要注意的是在处理序列相关时，工具变量也需要做相同的处理。

10.2 混合截面数据和面板数据的应用

使用2SLS处理混合横截面数据或面板数据时，与处理截面数据的方法并无差别。在经济学的实际应用过程中，面板数据是最常使用的，也是常通过IV或2SLS来解决内生性问题的。