MNIST 数据集——手写字符识别(未调用现有库，bp和knn，含代码)

目录
1 数据集分析 .......................................................................................................................................................2
2 数据集分割 .......................................................................................................................................................2
3 两种识别方法...................................................................................................................................................3
3.1 KNN .........................................................................................................................................................3
3.1.1 技术路线...................................................................................................................................3
3.1.2 数据取样...................................................................................................................................3
3.1.3 计算距离...................................................................................................................................4
3.1.4 预测 ............................................................................................................................................4
3.2 BP 神经网络 ..........................................................................................................................................4
3.2.1 技术路线...................................................................................................................................4
3.2.2 数据预处理 ..............................................................................................................................4
3.2.3 训练 ............................................................................................................................................5
3.2.4 预测 ............................................................................................................................................6
4 基于可视化的超参数调整............................................................................................................................6
4.1 KNN 模型 K 的调整 ............................................................................................................................6
4.2 BP 神经网络学习率调整 ...................................................................................................................7
5 选择合适超参数后的模型使用 ..................................................................................................................8
5.1 训练集与测试集 .................................................................................................................................8
5.2 KNN 模型 K=3 ......................................................................................................................................9
5.3 BP 神经网络学习率=0.1 ...................................................................................................................9
6 分析与总结 .................................................................................................................................................... 10
6.1 KNN 的优缺点 ................................................................................................................................... 10
6.2 BP 神经网络的优缺点..................................................................................................................... 10
6.3 对于本实验算法选取的分析 ....................................................................................................... 11

1 数据集分析
        MNIST 数据集是机器学习领域中非常经典的一个数据集，由 60000 个训练样本和 10000
个测试样本组成，每个样本都是一张 28 * 28 像素的灰度手写数字图片。
        数据格式为：

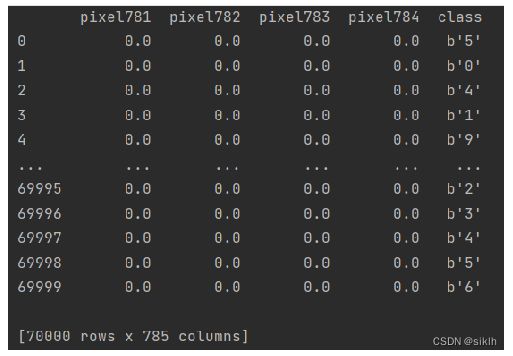
2 数据集分割
        由于数据量较大，因此，我们将提前对数据集进行处理，方便在训练时加载，减少程序
在数据加载的时间浪费。
        同时，为了方便对模型进行训练，我们将数据 data 与标签 label 进行单独保存。生成如
下数据集格式：

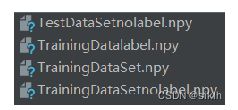
        其中，TrainingDataSetnolabel.npy 为训练数据，TrainingDatalabel.npy 为训练标签；
TestDataSetnolabel.npy 为测试数据，TestDatalabel.npy 为测试标签。

 

3 两种识别方法
3.1 KNN
3.1.1 技术路线

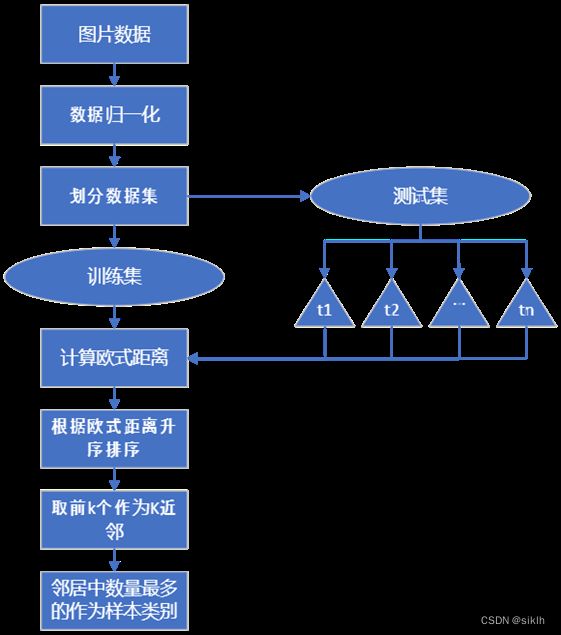
3.1.2 数据取样
        KNN 的全称是 K Nearest Neighbors，意思是 K 个最近的邻居。KNN 的原理就是当预
测一个新的值 x 的时候，根据它距离最近的 K 个点是什么类别来判断 x 属于哪个类别。
        如图所示：

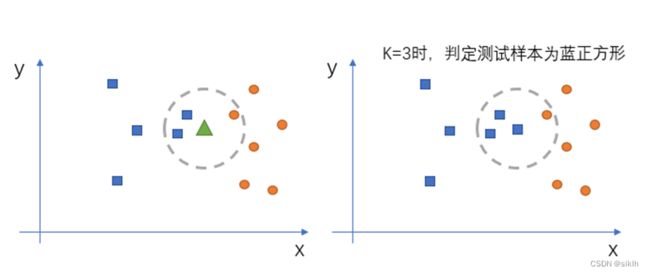
        为了更好地评估模型地性能，我们采用 5 折交叉验证来训练和使用模型。
        根据 KNN 的原理，由于其没有学习过程，测试集中每组数据的分类需要计算需要遍历
训练集中全部样本，因此计算量极大，为了缩短运行时间，更好的分析过程，我们取每折测

 试集中的前100个样本进行测试。

3.1.3 计算距离

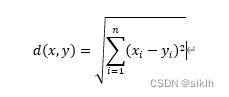
       要度量空间中点距离的话，有好几种度量方式，比如常见的曼哈顿距离计算、欧式距离计算等等。

        通常 KNN 算法中使用的是欧式距离，我们也采用欧氏距离进行衡量。

        其高维公式为：

 

3.1.4 预测

       KNN 算法最简单粗暴的就是将预测点与所有训练点的欧式距离进行计算，然后保存并排序，选出前面 K 个，看看哪种类别比较多，就认为预测数据属于哪一类。

3.2 BP神经网络

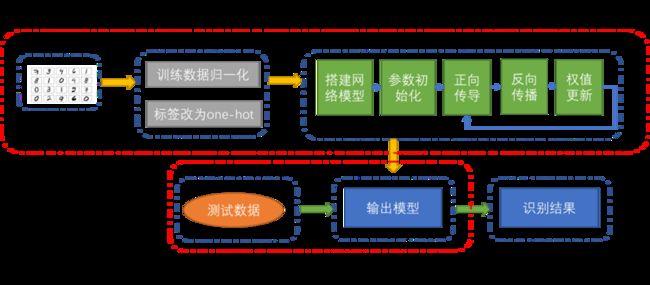
3.2.1 技术路线

 

 

3.2.2 数据预处理

       为了提高神经网络的训练速度，也加速训练的收敛，对训练数据进行归一化,把所有数据映射到0-1之间：

         由于训练任务是分类任务，因此需要对标签进行修改，最好改为one-hot编码格式，即[0,1,0,…,0,0]，但是由于我们选用的激活函数为Sigmund函数，因此，对于激活函数来说，生成0,1的输出是不可能的，会导致出现大的权重和饱和网络，所以我们使用0.01代替0，0.99代替1。

       至此，数据整形为如下格式：

       特征值：

[…，0.00000,0.00000,0.86275,0.63922,0.00000,0.00000,0.00000，…]

       标签：

[0.01, 0.01, 0.01, 0.01, 0.01, 0.99, 0.01, 0.01, 0.01, 0.01]

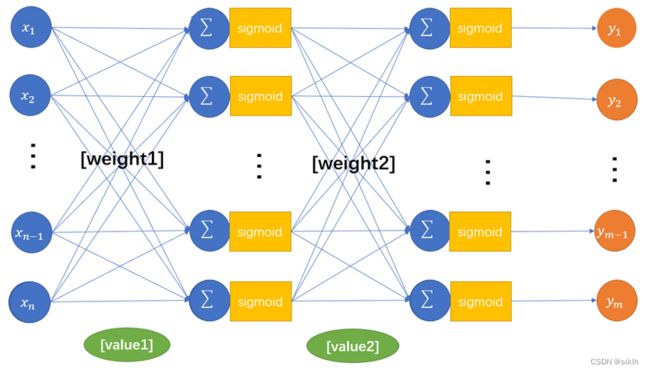
3.2.3 训练

我采用的BP神经网络模型如图所示：

 

 （1）参数初始化：

偏重值以高斯分布随机数初始化：

value1 = np.random.normal(0.0,pow(1,-0.5),(1,y))

value2 = np.random.normal(0.0,pow(1,-0.5),(1,z))

权重以高斯分布随机数初始化：

    weight1 = np.random.normal(0.0,pow(x,-0.5),(x,y))

    weight2 = np.random.normal(0.0,pow(y,-0.5),(y,z))

（2）正向传导：

输入与输出矩阵化：

inputset = np.mat(dataset[i])

        outputset = np.mat(labelset[i])

输入通过隐藏层：

input1 = np.dot(inputset,weight1)

        output2 = sigmoid(input1 - value1)

输入通过输出层：

        input2 = np.dot(output2,weight2)

        output3 = sigmoid(input2 - value2)

（3）反向传播：

因为sigmoid函数求导为：y’=y（1-y），因此反向传播为：

█(        @     a = np.multiply(output3,1 - output3)@g = np.multiply(a,outputset - output3)#输出层的反传播值)

█(             b = np.dot(g,np.transpose(weight2))@ c = np.multiply(output2,1 - output2)#@        e = np.multiply(b,c)#隐藏层的反传播值)

（4）权值更新，x为学习率：

█(        @   value1_change= -x * e@value2_change= -x * g@weight1_change= x * np.dot(np.transpose(inputset),e)@weight2_change = x * np.dot(np.transpose(output2),g)@ )

█(        @value1 += value1_change@value2+= value2_change@weight1+=weight1_change@weight2+ =weight2_change@ )

3.2.4 预测

使用已经训练好的权重和偏置值，对测试数据进行分类，对得到的形如 [0.01,0.01,0.01,0.01,0.01,0.99,0.01,0.01,0.01,0.01]的数据，获取最大值的序列号作为分类结果。

遍历测试集的所有数据，计算训练模型的准确率作为评价指标。

 

4 基于可视化的超参数调整

4.1 KNN模型K的调整

K的选取对模型影响巨大：

K越小越容易过拟合，当K=1时，这时只根据单个近邻进行预测，如果离目标点最近的一个点是噪声，就会出错，此时模型复杂度高，稳健性低，决策边界崎岖。

但是如果K取的过大，这时与目标点较远的样本点也会对预测起作用，就会导致欠拟合，此时模型变得简单，决策边界变平滑。

如果K=N的时候，那么就是取全部的样本点，这样预测新点时，最终结果都是取所有样本点中某分类下最多的点，分类模型就完全失效了。

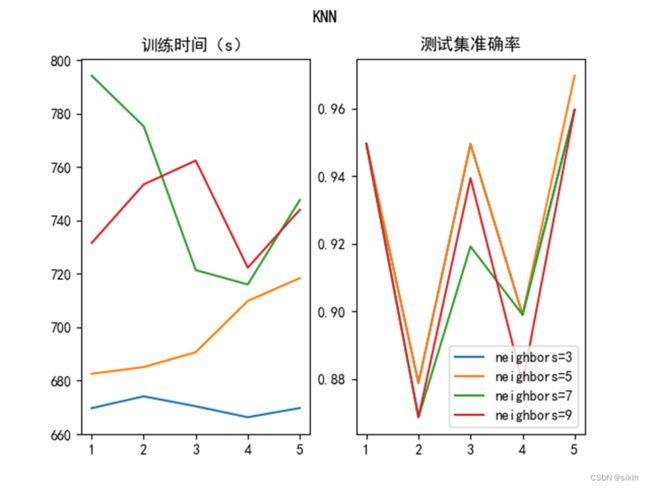
       我们调节K为3，5，7，9进行KNN的预测算法实现。利用5折交叉验证法进行训练，其结果如下：

 

K	平均训练时间（s）	平均测试集准确率
3	670.0661882400512	0.9272727272727271
5	697.3035259246826	0.9292929292929293
7	750.8898796558381	0.9191919191919192
9	742.7294894695282	0.9191919191919192

       我们可以发现：

       当K=3时，训练时间较短并且准确率也不错；

       当K=5，7，9时，训练时间逐渐增加并且准确率有一些波动。

       综上，K=3时，可以取得较好的分类效果。

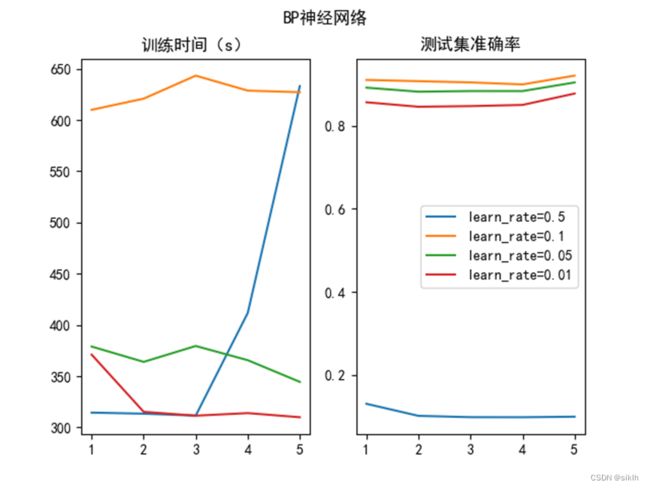
4.2 BP神经网络学习率调整

我们调整学习率为0.5，0.1，0.05，0.01，再利用5折交叉验证法进行训练，得到如下结果。

 

学习率	平均训练时间（s）	平均测试集准确率
0.5	626.0268793582916	0.1056
0.1	396.80884466171267	0.9082833333333333
0.05	324.2512463569641	0.88885
0.01	366.43220725059507	0.8552833333333332

我们可以发现：

学习率为0.5时，准确率奇低，训练时间较长，可见在训练集中发生了局部最优解；

学习率为0.1是我们正常选取的学习率；

学习率为0.01，0.05时，其准确率还不错。单相较于学习率为0.1时而言，仍欠佳。

此外，训练时间虽然有差异，但可以忽略不记。

我们可以发现，对于该模型而言，学习率对训练效果影响非常大，过大的学习率会导致模型找不到全局最优解，从而陷入局部最优解，使得模型泛化能力奇差；学习率过小，又会使模型可能过拟合。

因此，合适的学习率的选择是BP神经网络的调整关键。

5 选择合适超参数后的模型使用

5.1 训练集与测试集

使用60000个数据作为训练集，10000个数据作为测试集。

但由于KNN训练时间过长，训练集取全部，测试集取前100个数据。

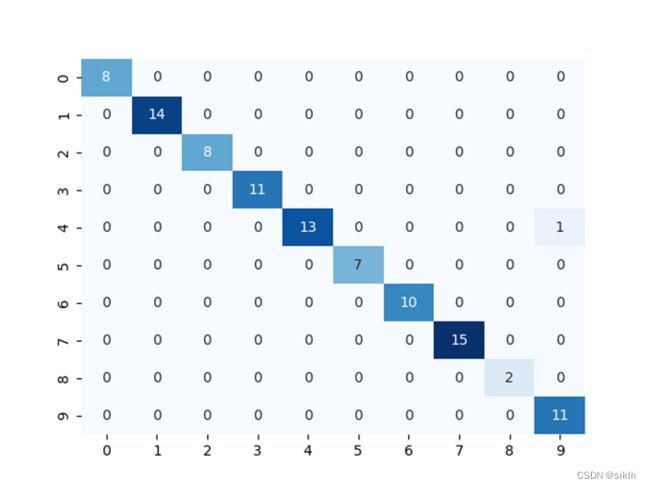
5.2 KNN模型K=3

混淆矩阵：

 

训练结果：

准确率：0.98989898989899

测试集时间：3604.773886680603 s

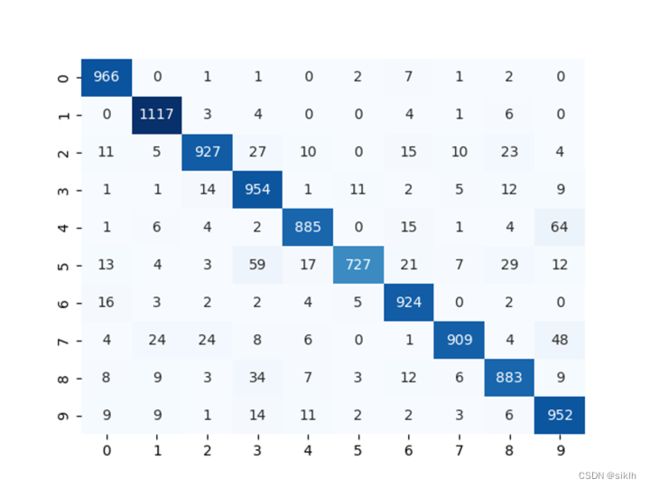
5.3 BP神经网络学习率=0.1

混淆矩阵：

 

训练结果：

准确率：0.9253

测试集时间：376.6516079902649 s

6 分析与总结

6.1 KNN的优缺点

优点：

• 简单有效
• 重新训练代价低
• 算法复杂度低
• 适合类域交叉样本
• 适用大样本自动分类

缺点：

• 惰性学习
• 类别分类不标准化
• 输出可解释性不强
• 不均衡性
• 计算量较大

6.2 BP神经网络的优缺点

优点：

非线性映射能力：BP神经网络实质上实现了一个从输入到输出的映射功能，数学理论证明三层的神经网络就能够以任意精度逼近任何非线性连续函数。这使得其特别适合于求解内部机制复杂的问题。

自学习和自适应能力：BP神经网络在训练时，能够通过学习自动提取输出、输出数据间的“合理规则”，并自适应的将学习内容记忆于网络的权值中。

泛化能力：所谓泛化能力是指在设计模式分类器时，即要考虑网络在保证对所需分类对象进行正确分类，还要关心网络在经过训练后，能否对未见过的模式或有噪声污染的模式，进行正确的分类。也即BP神经网络具有将学习成果应用于新知识的能力。

容错能力：BP神经网络在其局部的或者部分的神经元受到破坏后对全局的训练结果不会造成很大的影响，也就是说即使系统在受到局部损伤时还是可以正常工作的。

缺点：

局部极小化问题：从数学角度看，传统的 BP神经网络为一种局部搜索的优化方法，它要解决的是一个复杂非线性化问题，网络的权值是通过沿局部改善的方向逐渐进行调整的，这样会使算法陷入局部极值，权值收敛到局部极小点，从而导致网络训练失败。

BP 神经网络算法的收敛速度慢。

BP神经网络预测能力和训练能力的矛盾问题：预测能力也称泛化能力或者推广能力，而训练能力也称逼近能力或者学习能力。一般情况下，训练能力差时，预测能力也差，并且一定程度上，随着训练能力地提高，预测能力会得到提高。但这种趋势不是固定的，其有一个极限，当达到此极限时，随着训练能力的提高，预测能力反而会下降，也即出现所谓“过拟合”现象。

BP神经网络样本依赖性问题：网络模型的逼近和推广能力与学习样本的典型性密切相关，而从问题中选取典型样本实例组成训练集是一个很困难的问题。

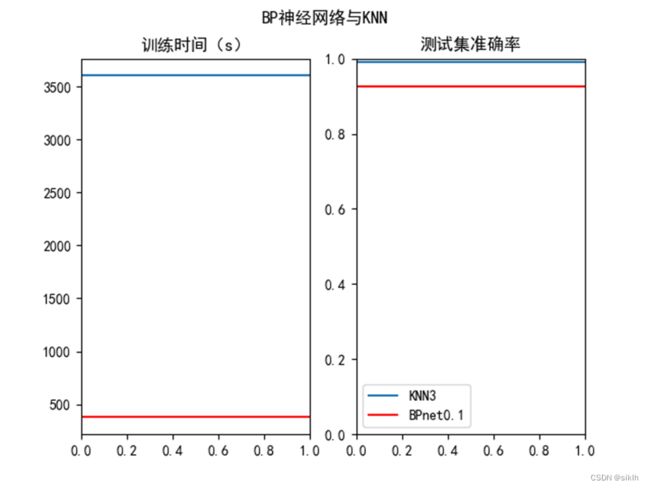
6.3 对于本实验算法选取的分析

算法	训练时间（s）	测试集准确率
KNN（K=3）	3604.773886680603	0.98989898989899
BP神经网络（学习率=0.1）	376.6516079902649	0.9253

 

       通过对KNN算法与BP神经网络算法的比较，我们发现这两种算法都可以起到较好的分类效果，就准确率而言，选择合适的K值的KNN算法可以得到极高的准确率。

       但是由于KNN需要在每个测试样本预测时计算与所有训练样本的欧氏距离来寻找K近邻，因此，计算量极大，耗时极长，因此，当需求要求分类的快速性与及时性时，或者测试样本很多时，KNN并不是一个合格的算法。

       BP神经网络在准确率上稍逊一筹，但是其时间在训练过程中被消耗，在测试时几乎没有延迟，它的快速性、及时性更好，面对大量测试样本时，也可以有极高的效率。

       综上，针对mnist数据集，单论分类效果而言，KNN更佳；当测试样本较大或对速度有需求时，BP神经网络更适合。

数据集：

请在openml.org网站下载手写字符识别识别数据集mnist_784

OpenML

也可使用sklearn.datasets.fetch_openml等函数进行数据获取

#处理数据
import numpy as np
from scipy.io import arff


# ————————————————————————————————一些必要的函数————————————————————————————————————————————————————————
# 读取数据集并进行划分，返回训练集与测试集
def LoadDataset(FileName, TrainingDataSetLen):
    TrainingDataSet = []
    TestDataSet = []
    dataset, meta = arff.loadarff(FileName)
    print('数据集总数量：', len(dataset))
    for x in range(len(dataset)):
        if x < TrainingDataSetLen:
            TrainingDataSet.append(dataset[x])
        else:
            TestDataSet.append(dataset[x])
    print("训练集数据数量:", len(TrainingDataSet))
    print("测试集数据数量:", len(TestDataSet))
    return TrainingDataSet, TestDataSet


# 用于将数据集中的形如 b’1‘ 格式转为 1 格式
def get_str_btw(s, f, b):
    par = s.partition(f)
    return (par[2].partition(b))[0][:]


# ——————————————————————————————读取.arff格式数据集，并划分训练集，测试集为60000，10000，并保存————————————————
TrainingDataSetLen = 60000
TrainingDataSet, TestDataSet = LoadDataset('../dataset/mnist_784.arff', TrainingDataSetLen)
np.save('TrainingDataSet', TrainingDataSet)
np.save('TestDataSet', TestDataSet)
print('保存成功！')

# ————————————————————————————————保存数据集中剔除标签后的数据——————————————————————————————————————————————
TrainingDataSet = np.load('TrainingDataSet.npy')
TestDataSet = np.load('TestDataSet.npy')
print("训练集数据数量:", len(TrainingDataSet))
print("测试集数据数量:", len(TestDataSet))
TrainingDataSet.tolist()
print(list(TrainingDataSet[0]))
TrainingDataSet_ = []
for i in range(len(TrainingDataSet)):
    x = list(TrainingDataSet[i])
    del (x[-1])
    # print(x)
    TrainingDataSet_.append(x)

TestDataSet_ = []
for i in range(len(TestDataSet)):
    x = list(TestDataSet[i])
    del (x[-1])
    # print(x)
    TestDataSet_.append(x)
np.save('TrainingDataSetnolabel', TrainingDataSet_)
np.save('TestDataSetnolabel', TestDataSet_)
print('保存成功！')

# ————————————————————————————————保存数据集里的标签——————————————————————————————————————————————————-————
TrainingDataSet = np.load('TrainingDataSet.npy')
TestDataSet = np.load('TestDataSet.npy')
print("训练集数据数量:", len(TrainingDataSet))
print("测试集数据数量:", len(TestDataSet))
TrainingDataSet.tolist()
# print(list(TrainingDataSet[0]))
TrainingDataSet_ = []
for i in range(len(TrainingDataSet)):
    x = list(TrainingDataSet[i])

    TrainingDataSet_.append([int(str(x[-1])[2])])
print(TrainingDataSet_)
TestDataSet_ = []
for i in range(len(TestDataSet)):
    x = list(TestDataSet[i])
    # del(x[-1])
    # print(x)
    TestDataSet_.append([int(str(x[-1])[2])])
print(TrainingDataSet_)
np.save('TrainingDatalabel', TrainingDataSet_)
np.save('TestDatalabel', TestDataSet_)
print('保存成功！')

#BPNET
import numpy as np
from matplotlib import pyplot as plt
import scipy.special as spc
import time as t


# ———————————————————————————————数据集加载—————————————————————————————————————————
def loaddataset():
    trainImage = np.load('../dataset/TrainingDataSetnolabel.npy')
    # 训练数据归一化
    trainImage = (trainImage - np.min(trainImage)) / (np.max(trainImage) - np.min(trainImage))
    trainLabel = np.load('../dataset/TrainingDatalabel.npy')
    testImage = np.load('../dataset/TestDataSetnolabel.npy')
    # 测试数据归一化
    testImage = (testImage - np.min(testImage)) / (np.max(testImage) - np.min(testImage))
    testLabel = np.load('../dataset/TestDatalabel.npy')
    return trainImage, trainLabel, testImage, testLabel


# ———————————————————————————————数据集分割为k折—————————————————————————————————————————
def k_fold(k, trainImage, trainLabel):
    foldtraindata = []
    foldtrainlabel = []
    num1 = len(trainLabel)
    for i in range(k):
        foldtraindata.append(trainImage[int((num1 / k) * i):int((num1 / k) * (i + 1)), :])
        foldtrainlabel.append(trainLabel[int((num1 / k) * i):int((num1 / k) * (i + 1))])
    return foldtraindata, foldtrainlabel


# ———————————————————————————————标签重制函数—————————————————————————————————————————
def adjustment_label(labelset):
    new_labelset = []
    for i in labelset:
        new_label = [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]
        new_label[int(i)] = 0.99
        new_labelset.append(new_label)
    return new_labelset


# ———————————————————————————————运算函数—————————————————————————————————————————
# sigmoid函数：f(x)= 1/(1+exp(-x))
def sigmoid(z):
    return spc.expit(z)


# ———————————————————————————————神经元网络—————————————————————————————————————————
# 参数初始化
def parameter_initialization(x, y, z):
    # 以高斯分布进行初始化偏置值
    value1 = np.random.normal(0.0, pow(1, -0.5), (1, y))
    value2 = np.random.normal(0.0, pow(1, -0.5), (1, z))
    # 以高斯分布进行初始化权重值
    weight1 = np.random.normal(0.0, pow(x, -0.5), (x, y))
    weight2 = np.random.normal(0.0, pow(y, -0.5), (y, z))
    return weight1, weight2, value1, value2


# 训练函数
def trainning(dataset, labelset, weight1, weight2, value1, value2, x):
    for i in range(len(dataset)):
        # 将输入与输出矩阵化，便于计算
        inputset = np.mat(dataset[i])
        outputset = np.mat(labelset[i])
        # 正向传导
        input1 = np.dot(inputset, weight1)
        output2 = sigmoid(input1 - value1)
        input2 = np.dot(output2, weight2)
        output3 = sigmoid(input2 - value2)
        # 反向传播
        # sigmoid函数求导：y’=y（1-y）
        a = np.multiply(output3, 1 - output3)
        g = np.multiply(a, outputset - output3)
        b = np.dot(g, np.transpose(weight2))
        c = np.multiply(output2, 1 - output2)
        e = np.multiply(b, c)
        # 权值更新，x为学习率
        value1_change = -x * e
        value2_change = -x * g
        weight1_change = x * np.dot(np.transpose(inputset), e)
        weight2_change = x * np.dot(np.transpose(output2), g)

        value1 += value1_change
        value2 += value2_change
        weight1 += weight1_change
        weight2 += weight2_change
    return weight1, weight2, value1, value2


# 测试函数
def Testing(dataset, labelset, weight1, weight2, value1, value2):
    rightcount = 0
    for i in range(len(dataset)):
        inputset = np.mat(dataset[i])
        outputset = np.mat(labelset[i])
        input1 = np.dot(inputset, weight1)
        output2 = sigmoid(input1 - value1)
        input2 = np.dot(output2, weight2)
        output3 = sigmoid(input2 - value2)

        label = np.argmax(output3)
        if int(label) == int(np.argmax(labelset[i])):
            rightcount += 1

    print("正确率为%f" % (rightcount / len(dataset)))
    return rightcount / len(dataset)


# —————————————————————————————————主函数———————————————————————————————————————

# 加载数据集
trainImage, trainLabel, testImage, testLabel = loaddataset()
# 调整训练集标签格式
trainLabel = adjustment_label(trainLabel)
# 将数据集分割为5折
foldtraindata, foldtrainlabel = k_fold(5, trainImage, trainLabel)

flag = [0, 1, 2, 3, 4]
# 用于记录训练时间
time = []
# 用于记录准确率
rightcount = []
# 开始训练测试
for ll in range(5):
    # 参数初始化
    weight1, weight2, value1, value2 = parameter_initialization(len(foldtraindata[0][0]), len(foldtraindata[0][0]),
                                                                len(foldtrainlabel[0][0]))
    # 记录训练开始时间
    start = t.time()
    flag_ = flag.copy()
    flag_.pop(ll)
    for i in range(1):
        for j in flag_:
            weight1, weight2, value1, value2 = trainning(foldtraindata[j], foldtrainlabel[j], weight1, weight2,
                                                         value1,
                                                         value2, 0.5)
        dataset_val = foldtraindata[ll]
        labelset_val = foldtrainlabel[ll]

        rightcount_ = Testing(dataset_val, labelset_val, weight1, weight2, value1, value2)
        # 记录准确率
        rightcount.append(rightcount_)
        # 记录程序结束时间
        finish = t.time()
        # 记录程序运行时间
        time.append(finish - start)

# 绘图
pici = [1, 2, 3, 4, 5]
plt.figure()
plt.subplot(1, 2, 1)
plt.plot(pici, time)
plt.subplot(1, 2, 2)
plt.plot(pici, rightcount)
plt.show()

#KNN
import math
import operator
from matplotlib import pyplot as plt
import numpy as np
import time as t


# ———————————————————————————————数据集加载—————————————————————————————————————————
from sklearn.decomposition import PCA


def loaddataset():
    trainImage = np.load('../dataset/TrainingDataSetnolabel.npy')
    # 训练数据归一化
    trainImage = (trainImage - np.min(trainImage)) / (np.max(trainImage) - np.min(trainImage))
    trainLabel = np.load('../dataset/TrainingDatalabel.npy')
    testImage = np.load('../dataset/TestDataSetnolabel.npy')
    # 测试数据归一化
    testImage = (testImage - np.min(testImage)) / (np.max(testImage) - np.min(testImage))
    testLabel = np.load('../dataset/TestDatalabel.npy')
    return trainImage, trainLabel, testImage, testLabel


# ———————————————————————————————数据集分割为k折—————————————————————————————————————————
def k_fold(k, trainImage, trainLabel):
    foldtraindata = []
    foldtrainlabel = []

    num1 = len(trainLabel)

    for i in range(k):
        foldtraindata.append(trainImage[int((num1 / k) * i):int((num1 / k) * (i + 1)), :])
        foldtrainlabel.append(trainLabel[int((num1 / k) * i):int((num1 / k) * (i + 1))])

    return foldtraindata, foldtrainlabel


# ———————————————————————————————必要函数—————————————————————————————————————————
# 计算欧氏距离 x=((x1-y1)^2+...+(xn-yn)^2)^(1/2)
def EuclideanDistance(Instance1, Instance2, Length):
    Distance = 0
    for x in range(Length):
        Distance += (Instance1[x] - Instance2[x]) * (Instance1[x] - Instance2[x])
        EuclideanDistance =np.sqrt(Distance)
    return EuclideanDistance


# 计算最近的k个近邻
def GetNeighbors(TrainingSet, trainLabel, TestInstance, k):
    distances = []
    length = len(TestInstance)
    for x in range(len(TrainingSet)):
        dist = EuclideanDistance(TestInstance, TrainingSet[x], length)
        distances.append((list(TrainingSet[x]) + list(trainLabel[x]), dist))
    # 将全部训练样本按照计算的欧式距离升序排列，获取前k个，作为邻居
    distances.sort(key=operator.itemgetter(1))
    neighbors = []
    for x in range(k):
        neighbors.append(distances[x][0])  # 得到k个近邻
    return neighbors


# 计算测试样例属于哪个类别
# 邻居中数量最多的作为样本类别
def GetResponse(neighbors):
    classVotes = {}  # 定义一个字典，方便计算类别个数
    for x in range(len(neighbors)):
        response = neighbors[x][-1]
        if response in classVotes:
            classVotes[response] += 1
        else:
            classVotes[response] = 1
    sortedVotes = sorted(classVotes.items(), key=operator.itemgetter(1), reverse=True)  # 降序排列
    return sortedVotes[0][0]


# 计算准确率
def GetAccuracy(testSet, predictions):
    correct = 0
    for x in range(len(testSet)):
        if testSet[x] == predictions[x]:
            correct += 1
    return correct / len(testSet)


# ———————————————————————————————主函数—————————————————————————————————————————
# def main():
# 加载数据集
trainImage, trainLabel, testImage, testLabel = loaddataset()
# 将数据集分割为5折
foldtraindata, foldtrainlabel= k_fold(5, trainImage, trainLabel)
flag = [0, 1, 2, 3, 4]
# 用于记录训练时间
time = []
# 用于记录准确率
rightcount = []
# 开始测试
for ll in range(5):
    # 记录训练开始时间
    start = t.time()
    flag_ = flag.copy()
    flag_.pop(ll)
    TrainingData = np.vstack((foldtraindata[flag_[0]],foldtraindata[flag_[1]],foldtraindata[flag_[2]],foldtraindata[flag_[3]]))
    TrainingLabel= np.vstack((foldtrainlabel[flag_[0]],foldtrainlabel[flag_[1]],foldtrainlabel[flag_[2]],foldtrainlabel[flag_[3]]))
    TestData = foldtraindata[ll]
    predictions = []
    k = 3  # 计算最近的3个近邻
    # 测试集数据测试
    for x in range(100):
        # 计算测试样本与训练集各样本地欧氏距离
        neighbors = GetNeighbors(TrainingData, TrainingLabel, TestData[x], k)
        # 获取距离测试样本最近的k个邻居并获取预测值
        result = GetResponse(neighbors)
        predictions.append(result)
    accuracy = GetAccuracy(TrainingLabel[:99], predictions)
    print("Accuracy: ", accuracy)
    rightcount.append(accuracy)
    finish = t.time()
    time.append(finish - start)

pici = [1, 2, 3, 4, 5]
plt.figure()
plt.subplot(1, 2, 1)
plt.plot(pici, time)
plt.subplot(1, 2, 2)
plt.plot(pici, rightcount)
plt.show()