认知计算Cognitive Computing 各章总结
认知计算Cognitive Computing 各章总结
2022年西电人工智能学院认知计算考题涉及:
认知计算的goal(认知计算做的是什么)、前馈神经网络、反向传播、监督学习与无监督学习概述(没考具体算法)、面部情感识别(涉及到了时序数据和情感图像数据分别使用什么网络结构)、attention机制
有学姐整理了一些笔记,我觉得还不错,尤其是谷裕老师班级的:西电认知计算笔记
章节索引
- 认知计算Cognitive Computing 各章总结
-
- 一、绪论 Introduction
- 二、神经网络 Neural Network
-
- 1. 生物神经元
-
- 1.1 结构
- 1.2 信号传递
- 1.3 神经元的数学应用
- 2. 神经网络
-
- 2.1 前向传播
- 2.2 反向传播
- 三、Learning
-
- 1. Bayesian inference & leaning 贝叶斯理论
-
- 1.1 Frequentist statistics VS. Bayesian statistics
- 1.2 贝叶斯推理的优势:
- 1.3 贝叶斯定理:
- 1.4 贝叶斯推理过程
- 1.5 贝叶斯分类
- 1.6 贝叶斯网络
- 2. Supervised learning 监督学习
-
- 2.1 Logistic Regression
- 2.2 Support Vector Machine 支持向量机
- 2.3 K-nearest-neighbor KNN
- 2.4 Random Forest 随机森林
- 3. Unsupervised learning 无监督学习
-
- 3.1 K-means算法
- 3.2 Principal Component Analysis
- 3.3 Independent Component Analysis 独立成分分析
- 3.4 GAN 生成对抗网络
- 四、强化学习
-
- 1. Markov 决策
-
- 1.1 马尔可夫决策过程定义
- 1.2 强化学习的4元素
- 2. Dynamic programming 动态规划
-
- 2.1 value function 估计
- 2.2 policy 改进
- 3. Monte Carlo methods 蒙特卡洛法
- 4. Temporal-Difference methods 时序差分学习
- 五、时序模型:RNN&LSTM&Attention
-
- 1. RNN循环神经网络
- 2. LSTM
- 3. RNN条件生成模型
-
- 3.1 seq2seq
-
- Encoder
- Decoder
- 3.2 Attention
- 六、Emotion & Facial Expression
-
- 1. 面部编码/参数化
- 2. 面部表情识别
- 3. feature extraction
- 4. 分类
一、绪论 Introduction
-
neocortex(新皮质)是进化最晚的部分,并且是大部分思维发生处。neocortex中neurons的数量的neurons之间的synapses的数量惊人。神经元大概有20 billion,每个神经元与大约10 k其他神经元连接。
-
基本的神经信息处理机制:
Vision(机器视觉)、Attention、Dopamine and Reward(新旧事物、多巴胺调节)、
Memory(海马区)、Meaning(语义理解)、Task directed behavior(抵抗干扰、任务导向)
-
认知三个层次:
(1). Computational:正在执行什么计算、处理哪些信息;
(2). Algorithmic:计算是如何通过一系列信息处理步骤执行的;
(3). Implementational(实现):硬件如何实现这些算法
-
大脑结构
a. Hippocampus(海马区):学习和事件和事实相关的“每日”新记忆。
b. Amygdala(杏仁核):识别情绪上的显著刺激、加强基于奖励(惩罚)的运动和认知
c. Thalamus(丘脑):感觉信息到达新皮质的主要途径,对感知、注意力、运动控制、强化学习等发挥作用
d. Basal Ganglia(基底核):运动控制、强化学习、控制功能执行
e. Cerebellum(小脑):包含大脑50%的neuron,作用为运动协调、多数认知任务
f. Occipital lobe(枕叶):视觉处理(包含初级视觉皮层V1)
g. Temporal lobe(颞叶):听觉和语言处理区域,作用为学习阅读、语义知识理解
h. Frontal lobe(前叶):大脑的执行皮层,认知推理、计划、受情绪影响
i. Parietal lobe(顶叶): 编码空间位置、数字、数学、抽象关系、指导运动动作
-
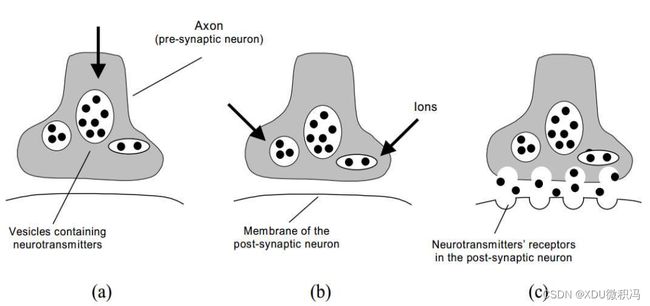
突触(Synapses)是发送神经元和接收神经元之间的连接点。大多数突触位于树突(dendrites)上,树突是神经元整合所有输入信号的大分支树。所有这些信号都流入主树突干和细胞体,信号的最终整合发生在细胞体中。
-
轴突(Axon)作为输出端,轴突会将信息(考虑阈值)传给与其相连的分支
二、神经网络 Neural Network
1. 生物神经元
1.1 结构
- 树突(dentrites):inputs – 输入接收器
- 细胞体(soma):输入信号求和
- 轴突(Axon):outputs – 输出发射器
- 突触(synapse):传输点
神经元在达到阈值后被激活,通过突触的电化学变化进行学习
1.2 信号传递
- 从突触接收上千个神经元的输入
- 输入的加权和
- 若超过阈值,则产生动作电位,沿着轴突输出,向下传播
1.3 神经元的数学应用
突触接受来自其他神经元的树突信号,胞体进行输入的加权求和,通过激活函数判断是否有信号向下传播。
2. 神经网络
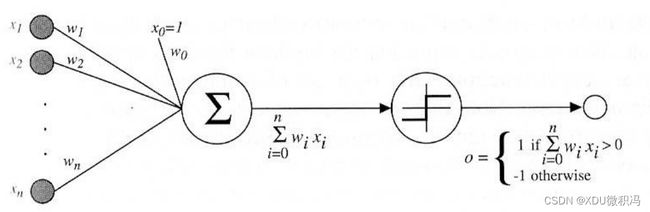
简单的应用生物神经元,可以推导出感知机:
y = ϕ ( ∑ i = 1 N w i x i + b ) y=\phi(\sum_{i=1}^{N}w_ix_i+b) y=ϕ(i=1∑Nwixi+b)
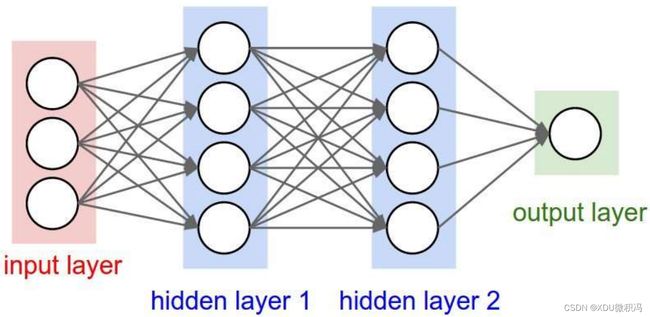
但发现它只能处理简单的线性可分问题,作用很局限,所以考虑多层的感知机演化而来的全连接网络,下图是三层网络结构:
2.1 前向传播
z j ( i + 1 ) = h ( ∑ i = 1 D w j i ( i ) ⋅ z i ( i ) + b ) = h ( ∑ i = 0 D w j i ( i ) ⋅ z i ( i ) ) z_j^{(i+1)} = h(\sum_{i=1}^{D}w_{ji}^{(i)}\cdot z_i^{(i)}+b)=h(\sum_{i=0}^{D}w_{ji}^{(i)}\cdot z_i^{(i)}) zj(i+1)=h(i=1∑Dwji(i)⋅zi(i)+b)=h(i=0∑Dwji(i)⋅zi(i))
在网络中,前一层的每一个输入 z j ( i ) z_j^{(i)} zj(i)通过加权求和,并经过非线性激活得到本层第 j j j个节点的值。我们以三层网络为例,可以得到输出 y k y_k yk关于输入 x i x_i xi的关系:
y k = σ ( a k ) = σ ( ∑ j = 0 M w k j ( 2 ) z j ( 2 ) ) = σ ( ∑ j = 0 M w k j ( 2 ) ⋅ h ( ∑ i = 0 D w j i ( 1 ) x i ) ) \begin{aligned} y_k &= \sigma(a_k) = \sigma(\sum_{j=0}^{M}w_{kj}^{(2)}z_j^{(2)}) \\ &= \sigma(\sum_{j=0}^{M}w_{kj}^{(2)}\cdot h(\sum_{i=0}^{D}w_{ji}^{(1)}x_i)) \end{aligned} yk=σ(ak)=σ(j=0∑Mwkj(2)zj(2))=σ(j=0∑Mwkj(2)⋅h(i=0∑Dwji(1)xi))
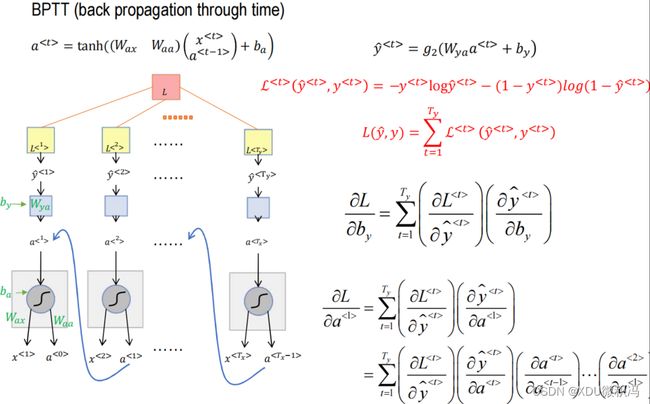
2.2 反向传播
由于权重参数需要更新,所以反向传播从输出结点开始,利用梯度信息从后往前更新各层参数。还是以三层网络为例,我们设 δ k \delta_k δk, δ j \delta_j δj是损失E关于 a k ( 2 ) a_k^{(2)} ak(2), a j ( 1 ) a_j^{(1)} aj(1)的函数,有
δ k = ∂ E ∂ a k ( 2 ) \delta_k=\frac{\partial E}{\partial a_k^{(2)}} δk=∂ak(2)∂E
δ j = ∂ E ∂ a j ( 1 ) = ∑ k ∂ E ∂ a k ( 2 ) ∂ a k ( 2 ) ∂ z j ( 2 ) ∂ z j ( 2 ) ∂ a j ( 1 ) = ∑ k δ k ⋅ w k j ( 2 ) ⋅ h ′ ( a j ( 1 ) ) = h ′ ( a j ( 1 ) ) ∑ k w k j ( 2 ) δ k \begin{aligned} \delta_j &= \frac{\partial E}{\partial a_j^{(1)}}=\sum_{k}\frac{\partial E}{\partial a_k^{(2)}}\frac{\partial a_k^{(2)}}{\partial z_j^{(2)}}\frac{\partial z_j^{(2)}}{\partial a_j^{(1)}}\\ &= \sum_{k}\delta_k \cdot w_{kj}^{(2)}\cdot h^{'}(a_j^{(1)})\\ &= h^{'}(a_j^{(1)})\sum_k{w_{kj}^{(2)}\delta_k} \end{aligned} δj=∂aj(1)∂E=k∑∂ak(2)∂E∂zj(2)∂ak(2)∂aj(1)∂zj(2)=k∑δk⋅wkj(2)⋅h′(aj(1))=h′(aj(1))k∑wkj(2)δk
可以发现,当算出 δ k \delta_k δk后, δ j \delta_j δj就可以可以求解了,那么当层数变多后,依次类推即可。所以反向传播的步骤如下:
- 计算输出层每个节点的 δ k \delta_k δk;
- 进行反向传播,例如隐含层的 δ j \delta_j δj可以由输出层的 δ k \delta_k δk计算得出,每一个层的 δ \delta δ可以由上一层的结果得出;
- 求参数 w j i w_{ji} wji的偏导数,公式如下:
∂ E ∂ w j i = δ j ⋅ z j \frac{\partial E}{\partial w_{ji}}=\delta_j \cdot z_j ∂wji∂E=δj⋅zj
神经网络采用随机梯度下降法更新,公式为:
θ ( t + 1 ) = θ ( t ) − η ∇ w j i E ( f θ ( x ) , y ) \theta^{(t+1)} = \theta^{(t)} - \eta \nabla_{w_{ji}}E(f_{\theta}(x), y) θ(t+1)=θ(t)−η∇wjiE(fθ(x),y)
三、Learning
1. Bayesian inference & leaning 贝叶斯理论
1.1 Frequentist statistics VS. Bayesian statistics
- 频率学派:利用样本信息预测总体,求在大量试验中某个事件的相对频率的极限;认为概率是长期的相对频率
- 贝叶斯学派:用先验信息、样本信息预测整体;认为概率是主观信念的程度
1.2 贝叶斯推理的优势:
贝叶斯推理方法在以下情况会十分有效:
- 数据有限;
- 担心过拟合;
- 显然某些事实比其他事实更有可能,但数据集中不包含该事实;
- 希望准确地知道某些事实的可能性(而不是仅仅选择最可能的事实)
1.3 贝叶斯定理:
贝叶斯定理比较常见,直接附上贝叶斯公式:
p ( B i ∣ A ) = p ( A ∣ B i ) p ( B i ) p ( A ) = p ( A ∣ B i ) p ( B i ) ∑ j p ( A ∣ B j ) p ( B j ) p(B_i|A) = \frac{p(A|B_i)p(B_i)}{p(A)} = \frac{p(A|B_i)p(B_i)}{\sum_jp(A|B_j)p(B_j)} p(Bi∣A)=p(A)p(A∣Bi)p(Bi)=∑jp(A∣Bj)p(Bj)p(A∣Bi)p(Bi)
将其应用于model,可有:
P ( model | data ) = P ( data | model ) P ( model ) P ( data ) ⟹ P ( θ | X ) = P ( X | θ ) P ( θ ) P ( X ) P(\text{model | data})=\frac{P(\text{data | model})P(\text{model})}{P(\text{data})} \Longrightarrow P(\theta \text{ | X})=\frac{P(\text{X | }\theta)P(\theta)}{P(X)} P(model | data)=P(data)P(data | model)P(model)⟹P(θ | X)=P(X)P(X | θ)P(θ)
其中, p ( θ ) p(\theta) p(θ)被称为先验概率, p ( X ∣ θ ) p(X|\theta) p(X∣θ)被称为似然函数, P ( θ | X ) P(\theta \text{ | X}) P(θ | X)被称为后验概率。
-
先验(Prior):你对未知数据的假设(hypothesis)
-
后验(Posterior):通过新数据,更新后的你的假设
-
为什么叫似然函数呢?若假设数据点 X 1 , . . . , X n X_1,...,X_n X1,...,Xn独立同分布,那么
p ( X ∣ θ ) = ∏ i = 1 n p ( X i ∣ θ ) = L ( θ ∣ X 1 , . . . , X n ) p(X|\theta) = \prod_{i=1}^{n}p(X_i|\theta) = L(\theta|X_1,...,X_n) p(X∣θ)=i=1∏np(Xi∣θ)=L(θ∣X1,...,Xn)
即他们的表达式形式是一样的。
最后,考虑式子(9)的分母是归一化的,可以直接忽略,那么可以得到:
P ( θ ∣ X ) ∝ P ( X ∣ θ ) P ( θ ) , 即 后 验 ∝ 似 然 × 先 验 P(\theta|X) \propto P(X|\theta)P(\theta),\qquad即后验\propto 似然\times先验 P(θ∣X)∝P(X∣θ)P(θ),即后验∝似然×先验
如果我们想要得到最大后验(MAP),等价于 a r g max P ( X ∣ θ ) P ( θ ) arg\max P(X|\theta)P(\theta) argmaxP(X∣θ)P(θ)
1.4 贝叶斯推理过程
-
以先验分布 () 的形式编码您对 的初始信念。
-
通过实验、观察、查询等方式收集数据 X X X。
-
使用贝叶定理将信念更新为后验分布
P n e w ( θ ) = P ( θ ∣ X ) ∝ P ( X ∣ θ ) ⋅ P o l d ( θ ) P^{new}(\theta) = P(\theta | X) \propto P(X|\theta)\cdot P^{old}(\theta) Pnew(θ)=P(θ∣X)∝P(X∣θ)⋅Pold(θ) -
随着更多数据可用,重复整个过程。
1.5 贝叶斯分类
设 y = { c 1 , . . . , c N } y=\{ c_1,...,c_N \} y={c1,...,cN},则贝叶斯分类的决策函数为:
h ( x ) = a r g max c ∈ y P ( c ) ∏ i = 1 d P ( x i ∣ c ) h(\pmb{x})=arg\max \limits_{c\in y} P(c) \prod_{i=1}^{d}P(x_i|c) h(xxx)=argc∈ymaxP(c)i=1∏dP(xi∣c)
这个公式的由来可以从最小错误率的观点推导:
设我们的损失为:
R ( c i ∣ x ) = ∑ j = 1 N λ i j P ( c j ∣ x ) , λ i j = { 0 , if i = j 1 , otherwise R(c_i|\pmb{x})=\sum_{j=1}^N \lambda_{ij}P(c_j|\pmb{x}),\quad \lambda_{ij}= \begin{cases} 0,\quad \text{if }\ i=j\\ 1,\quad \text{otherwise} \end{cases} R(ci∣xxx)=j=1∑NλijP(cj∣xxx),λij={0,if i=j1,otherwise
从 λ \lambda λ的定义来看,所有的损失均来自于i≠j的部分,那么要让损失最小,肯定要让i=j的部分尽可能大,故应该最大化后验概率,于是得证。
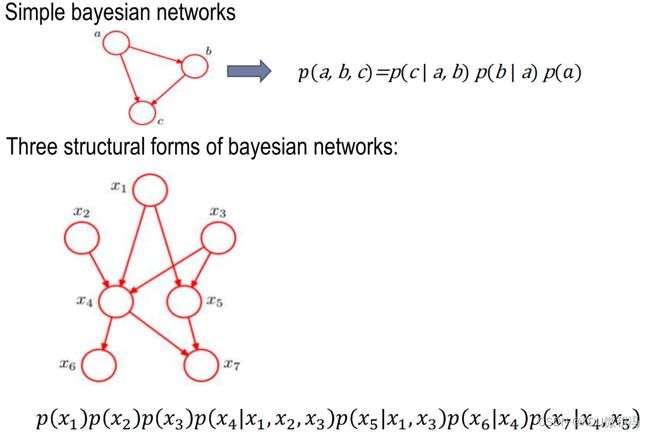
1.6 贝叶斯网络
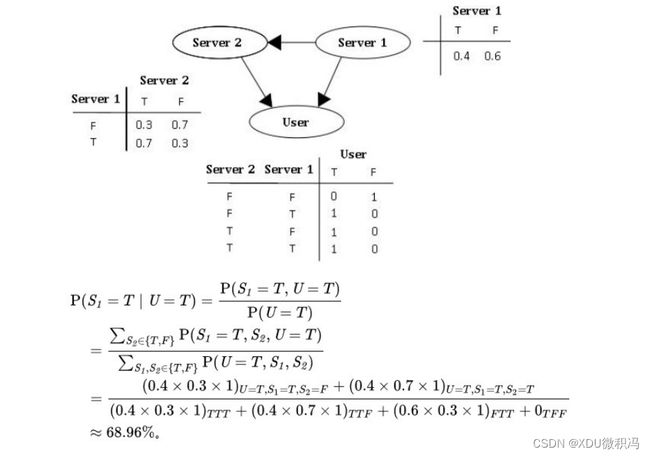
涉及联合概率,由于PPT中介绍的不多,这里直接附上便于理解的网络结构和计算例题:
2. Supervised learning 监督学习
监督学习的数据由input和期望的output组成,即数据是有标签的。
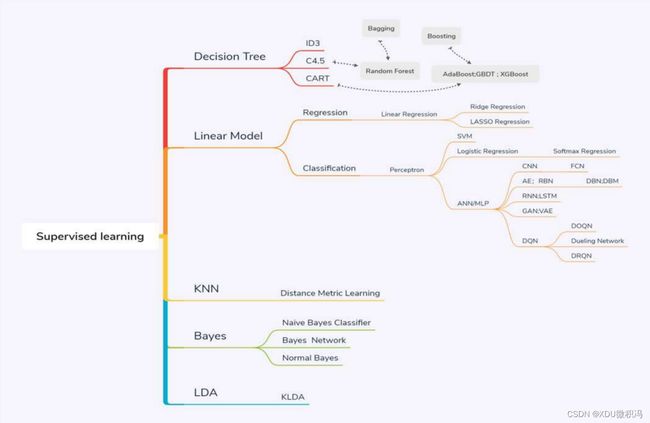
本章会接触到的经典的监督学习模型如下所示,注意关注logistics回归和KNN,其它涉及理论复杂,不会手推:
监督学习的训练和预测步骤:
2.1 Logistic Regression
- 是一个概率判别式、线性分类方法
logistic回归采用sigmoid函数把函数值限制在了0-1之间,表达式为:
{ P ( c 1 ∣ ϕ ) = σ ( w T ϕ ) P ( c 2 ∣ ϕ ) = 1 − P ( c 1 ∣ ϕ ) \begin{cases} P(c_1|\phi)=\sigma(\pmb{w}^T\phi) \\ P(c_2|\phi) = 1-P(c_1|\phi) \end{cases} {P(c1∣ϕ)=σ(wwwTϕ)P(c2∣ϕ)=1−P(c1∣ϕ)
对于一个数据集 ϕ n \phi_n ϕn和目标输出 t n ∈ { 0 , 1 } t_n\in\{0,1\} tn∈{0,1},似然函数可写为:
P ( t ∣ w ) = ∏ i = 1 N y n t n ( 1 − y n ) 1 − t n P(\pmb{t}|w) = \prod_{i=1}^{N}y_n^{t_n}(1-y_n)^{1-t_n} P(ttt∣w)=i=1∏Nyntn(1−yn)1−tn
通过取似然函数的负对数,可以获得交叉熵损失函数:
E ( w ) = − ∑ n = 1 N t n ln y n + ( 1 − t n ) ln ( 1 − y n ) σ ′ = y n ′ = σ ( 1 − σ ) = y n ( 1 − y n ) E(\pmb{w})=-\sum_{n=1}^{N}t_n\ln y_n+(1-t_n)\ln (1-y_n) \\ \sigma'=y_n^{'} = \sigma(1-\sigma)=y_n(1-y_n) E(www)=−n=1∑Ntnlnyn+(1−tn)ln(1−yn)σ′=yn′=σ(1−σ)=yn(1−yn)
求偏导有:
∇ E ( w ) = ∑ n = 1 N { y n − t n } ϕ n \nabla E(\pmb{w}) =\sum_{n=1}^N \{y_n-t_n\}\phi_n ∇E(www)=n=1∑N{yn−tn}ϕn
2.2 Support Vector Machine 支持向量机
- 以二分类为例
考虑线性的超平面: w T ϕ ( x ) + b = 0 w^T\phi(\pmb{x})+b=0 wTϕ(xxx)+b=0,如果它可以正确的分离训练集,那么对任意的数据 ( x n , t n ) (x_n,t_n) (xn,tn),都有若 t n = + 1 t_n=+1 tn=+1有 w T ϕ ( x ) + b > 0 w^T\phi(\pmb{x})+b>0 wTϕ(xxx)+b>0,若 t n = − 1 t_n=-1 tn=−1有 w T ϕ ( x ) + b < 0 w^T\phi(\pmb{x})+b<0 wTϕ(xxx)+b<0。不失一般性,由下式成立:
{ w T ϕ ( x n ) + b ≥ + 1 , t n = + 1 w T ϕ ( x n ) + b ≤ − 1 , t n = − 1 \begin{cases} w^T\phi(x_n)+b \geq+1,\quad t_n=+1 \\ w^T\phi(x_n)+b \leq-1,\quad t_n=-1 \end{cases} {wTϕ(xn)+b≥+1,tn=+1wTϕ(xn)+b≤−1,tn=−1
上式可以看出一个完美的模型满足:
( w T ϕ ( x n ) + b ) ⋅ t n ≥ 1 , ∀ n ∈ { 1 , . . . , N } (w^T\phi(x_n)+b)\cdot t_n \geq 1,\quad \forall n \in \{1,...,N\} (wTϕ(xn)+b)⋅tn≥1,∀n∈{1,...,N}
我们的决策目标是:使两类到分类面的最短距离(即间隔)尽可能大,且各样本分类都正确,则可表示为:
{ max 2 ∥ w ∥ o r min 1 2 ∥ w ∥ s.t. t n ( w T ϕ ( x n ) + b ) ≥ 1 \begin{cases} \ \max\ \frac{2}{\lVert w \rVert} or \ \min \frac{1}{2}\lVert w\rVert\\ \text{s.t.}\ \ t_n(w^T\phi(x_n)+b) \geq 1 \end{cases} { max ∥w∥2or min21∥w∥s.t. tn(wTϕ(xn)+b)≥1
通过拉格朗日乘数法:
L ( w , b , α ) = 1 2 ∥ w ∥ − ∑ n = 1 N α n { t n ( w t ϕ ( x n ) + b ) − 1 } L(w,b,\alpha)=\frac{1}{2}\lVert w\rVert - \sum_{n=1}^{N}\alpha_n\{t_n(w^t\phi(x_n)+b)-1 \} L(w,b,α)=21∥w∥−n=1∑Nαn{tn(wtϕ(xn)+b)−1}
求解w和b的偏导数即有:
max ∑ n = 1 N α n − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j t i t j ϕ ( x i ) T ϕ ( x i ) s . t . { ∑ n = 1 N α n t n = 0 α i ≥ 0 , i = 1 , . . . , N \max \sum_{n=1}^{N}\alpha_n-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jt_it_j\phi(x_i)^T\phi(x_i) \\ s.t. \begin{cases} \sum_{n=1}^N\alpha_nt_n=0\\ \\ \alpha_i \geq 0,\quad i=1,...,N \end{cases} maxn=1∑Nαn−21i=1∑Nj=1∑Nαiαjtitjϕ(xi)Tϕ(xi)s.t.⎩⎪⎨⎪⎧∑n=1Nαntn=0αi≥0,i=1,...,N
2.3 K-nearest-neighbor KNN
- 分类时:选择K个最近样本进行”投票“,选出现频率最高的类 (可加权)
- 回归时:选择K个最近样本,取均值(可加权)
决策函数(设 N k ( x ) N_k(\pmb{x}) Nk(xxx)是K个最近的样本集):
y = a r g max ∑ x i ∈ N k ( x ) I ( y i = c j ) y = arg\max\sum_{x_i\in N_k(\pmb{x})}I(y_i=c_j) y=argmaxxi∈Nk(xxx)∑I(yi=cj)
错分概率:
P ( e r r o r ) = 1 − ∑ c ∈ y P ( c ∣ x ) P ( c ∣ N k ( x ) ) P(error)=1-\sum_{c\in y}P(c|\pmb x)P(c|N_k(\pmb x)) P(error)=1−c∈y∑P(c∣xxx)P(c∣Nk(xxx))
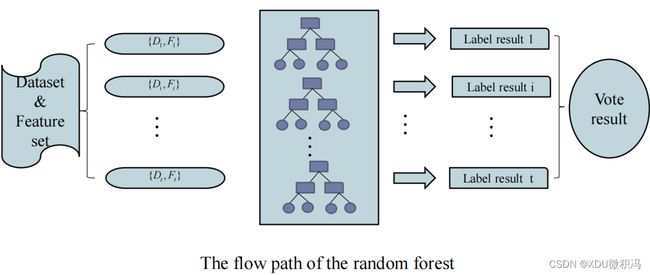
2.4 Random Forest 随机森林
-
Bagging算法的特殊例子
-
什么是Bagging?简单来讲就是在一次采样中,n个数据有放回地取n次,进行m次采样的过程。极限情况总采样可覆盖63.2%的数据。我们用每次采样的n个数据训练一个model,那么总共就有m个model,我们把这m个model组合在一起,这就是Bagging。
-
RF算法除了Bagging外,还在每次采样后的model(使用决策树模型)训练过程中加入随机属性选项,即在d个feature中每次随机选择k个,在k个feature里寻找最优feature。
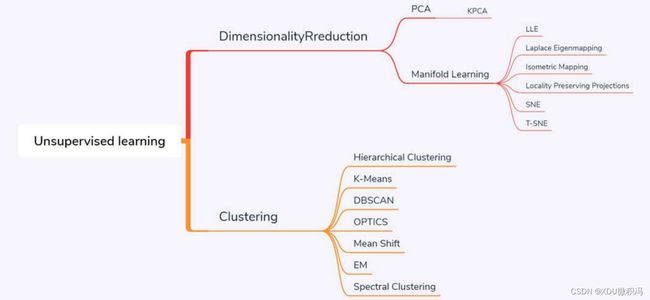
3. Unsupervised learning 无监督学习
- 无监督学习所使用的实例是未标记(即没有标签)的
3.1 K-means算法
示例及迭代可视化:
3.2 Principal Component Analysis
-
投影方差最大化、投影误差最小化 – 可以以此为策略推出PCA公式
-
本质上是求解得出最大的m(降维维度)个特征值的特征向量的过程。
3.3 Independent Component Analysis 独立成分分析
3.4 GAN 生成对抗网络
- 由一个生成网络和一个判别网络组成,通过两个网络相互作用来学习。其中生成网络从潜在空间随机采样作为输入,其输出要尽可能模拟训练集的真实样本;判别函数则接收生成网络的输出和真实样本作为输入,其尽可能将输入的两个样本区分开来。
判别公式:
min G max D V ( D , G ) = E x ∼ p d a t a ( x ) { log D ( x ) } + E z ∼ p z ( z ) { log ( 1 − D ( G ( z ) ) ) } \min\limits_{G}\max\limits_D\ V(D,G)=E_{\pmb x\sim p_{data}(x)}\{\log D(\pmb x)\}+E_{\pmb z\sim p_z(z)}\{\log(1-D(G(\pmb z)))\} GminDmax V(D,G)=Exxx∼pdata(x){logD(xxx)}+Ezzz∼pz(z){log(1−D(G(zzz)))}
G代表生成器,D代表判别器,所以该网络期望最大化判别器辨别样本是否真实的能力,最小化生成器生成的样本与真实样本的差异。
四、强化学习
- Data: state-action pairs
- Goal: 通过多个时间步骤实现长期的累积Reward最大化
- 上图的含义是:在Agent在每一步t,采取行动 a t a_t at前先观察环境的状态 s t s_t st和奖励 r t r_t rt,Agent做出的行动 a t a_t at会改变环境的状态和奖励,形成下一步t+1的状态 s t + 1 s_{t+1} st+1和奖励 r t + 1 r_{t+1} rt+1
total reward: R t = ∑ i = t ∞ r i = r t + r t + 1 + . . . + r t + n + . . . \text{total reward:}\quad R_t=\sum_{i=t}^{\infty}r_i=r_t+r_{t+1}+...+r_{t+n}+... total reward:Rt=i=t∑∞ri=rt+rt+1+...+rt+n+...
强化学习的4个元素:
- Policy:做什么
- Reward:什么是好的
- Value Function:预测reward
- Model:即每个步骤的顺序,what follows what
1. Markov 决策
马尔可夫决策过程正式描述了强化学习的环境,即:
- 环境完全可观察
- 当前状态完全表征了过程(即与历史无关)
1.1 马尔可夫决策过程定义
状态 S t S_t St是马尔科夫的,当且仅当下一状态仅与当前状态有关,与历史无关:
P [ S t + 1 ∣ S t ] = P [ S t + 1 ∣ S 1 , . . . , S t ] P[S_{t+1}|S_t]=P[S_{t+1}|S_1,...,S_t] P[St+1∣St]=P[St+1∣S1,...,St]
MDP(马尔可夫决策过程)是一个状态、动作、奖励上的随机过程,由 < S , A , P , R , γ >
-
S S S是有限状态集
-
A A A是一组有限的动作
-
P P P是状态转移概率矩阵
P s s ′ a = P ( S t + 1 = s ′ ∣ S t = s , A t = a ) P_{ss'}^a=P(S_{t+1}=s'| S_t=s,\ A_t=a) Pss′a=P(St+1=s′∣St=s, At=a) -
R R R是奖励函数
R s a = E ( R t + 1 ∣ S t = s , A t = a ) R_s^a=E(R_{t+1}|S_t=s, A_t=a) Rsa=E(Rt+1∣St=s,At=a) -
γ \gamma γ是衰减系数, γ ∈ [ 0 , 1 ] \gamma \in[0,1] γ∈[0,1]
带有衰减的总体奖励函数为:
R t = ∑ i = t ∞ γ i r i = γ t r t + γ t + 1 r t + 1 + . . . R_t = \sum_{i=t}^{\infty}\gamma^ir_i=\gamma^tr_t+\gamma^{t+1}r_{t+1}+... Rt=i=t∑∞γiri=γtrt+γt+1rt+1+...
1.2 强化学习的4元素
强化学习 { Policy based Value based Model based \text{强化学习}\begin{cases} \text{Policy based}\\ \text{Value based}\\ \text{Model based} \end{cases} 强化学习⎩⎪⎨⎪⎧Policy basedValue basedModel based
基于是否model-based可以对MDP进行如下分类:
-
Reward: 环境关于state的reward函数:
-
立即reward: R s = E π ( R t + 1 ∣ S t = s ) R_s=E_{\pi}(R_{t+1}|S_t=s) Rs=Eπ(Rt+1∣St=s)
其中下标 π \pi π代表了 A t = π ( s ) A_t=\pi(s) At=π(s)的限制条件
-
带有衰减的长期reward: G t = ∑ k = 0 ∞ γ k R t + k + 1 G_t=\sum_{k=0}^{\infty}\gamma^kR_{t+k+1} Gt=∑k=0∞γkRt+k+1
-
-
Policy: Agent的action(关于state的)函数
- 确定性policy: a = π ( s ) a=\pi(s) a=π(s)
- 随机性policy: π ( a ∣ s ) = P ( G t ∣ A t = a , S t = s ) \pi(a|s)=P(G_t|A_t=a,S_t=s) π(a∣s)=P(Gt∣At=a,St=s)
Agent需要policy π ( s ) \pi(s) π(s)以推断在该状态下的最佳action
-
Value Function: 执行action π \pi π后瞬时+未来总回报的期望值
- State: V π ( s ) = E π ( G t ∣ S t = s ) V_\pi(s)=E_\pi(G_t|S_t=s) Vπ(s)=Eπ(Gt∣St=s)
- State-action: Q π ( s , a ) = E π ( G t ∣ S t = s , A t = a ) Q_\pi(s,a)=E_\pi(G_t|S_t=s,A_t=a) Qπ(s,a)=Eπ(Gt∣St=s,At=a)
最佳的value function:
-
policy需要选择一个最大化未来回报的行动,对于state-action,有:
π ∗ ( s ) = arg max a Q ∗ ( s , a ) \pi^*(s)=\text{arg}\max\limits_aQ^*(s,a) π∗(s)=argamaxQ∗(s,a) -
对于state value function,我们直接寻找最优的 π \pi π,即:
V ∗ ( s ) = max π V π ( s ) V^*(s)=\max\limits_{\pi}V_\pi(s) V∗(s)=πmaxVπ(s)V ∗ ( s ) = max a ∑ s ′ P s s ′ a ( r s s ′ a + γ V ∗ ( s ′ ) ) ( B e l l m a n 最 优 性 方 程 ) V^*(s)=\max\limits_{a}\sum_{s'}P_{ss'}^a(r_{ss'}^a+\gamma V^*(s'))\qquad (Bellman最优性方程) V∗(s)=amaxs′∑Pss′a(rss′a+γV∗(s′))(Bellman最优性方程)
-
Model(如MDP): 可以直接预测环境下一步的变化。它有确定的状态转移概率矩阵 P s s ′ a P_{ss'}^a Pss′a和奖励函数 R s a R_s^a Rsa
2. Dynamic programming 动态规划
- 解决有最优子结构、重叠子问题属性的问题
- 需要知道整个环境(即model-based),需要value function V ( s ) V(s) V(s)寻找最优策略,并且使用多次重复采样(bootstrapping)对 V ( s ) V(s) V(s)估计
2.1 value function 估计
考虑简单的T步累计奖赏,那么由于MDP有马尔可夫性质,因此value function具有简单的递归形式:
V T π ( s ) = E π ( 1 T ∑ t = 1 T r t ∣ s 0 = s ) = E π ( 1 T r 1 + T − 1 T 1 T − 1 ∑ t = 2 T r t ∣ s 0 = s ) = ∑ a ∈ A π ( s , a ) ∑ s ′ ∈ S P s s ′ a ( 1 T R s s ′ a + T − 1 T E π [ 1 T − 1 ∑ t = 1 T − 1 r t ∣ s 0 = s ′ ] ) = ∑ a ∈ A π ( s , a ) ∑ s ′ ∈ S P s s ′ a ( 1 T R s s ′ a + T − 1 T V T − 1 π ( s ′ ) ) \begin{aligned} V_T^\pi(s) &= E_\pi(\frac{1}{T}\sum_{t=1}^{T}r_t|s_0=s)\\ &= E_\pi(\frac{1}{T}r_1+\frac{T-1}{T}\frac{1}{T-1}\sum_{t=2}^{T}r_t\ |\ s_0=s)\\ &= \sum_{a\in A}\pi(s,a)\sum_{s'\in S}P_{ss'}^a(\frac{1}{T}R_{ss'}^a+\frac{T-1}{T}E_\pi[\frac{1}{T-1}\sum_{t=1}^{T-1}r_t\ |\ s_0=s'])\\ &= \sum_{a\in A}\pi(s,a)\sum_{s'\in S}P_{ss'}^a(\frac{1}{T}R_{ss'}^a+\frac{T-1}{T}V_{T-1}^{\pi}(s'))\\ \end{aligned} VTπ(s)=Eπ(T1t=1∑Trt∣s0=s)=Eπ(T1r1+TT−1T−11t=2∑Trt ∣ s0=s)=a∈A∑π(s,a)s′∈S∑Pss′a(T1Rss′a+TT−1Eπ[T−11t=1∑T−1rt ∣ s0=s′])=a∈A∑π(s,a)s′∈S∑Pss′a(T1Rss′a+TT−1VT−1π(s′))
类似地,对于 γ \gamma γ折扣累积奖赏,有:
V γ π ( s ) = ∑ a ∈ A π ( s , a ) ∑ s ′ ∈ S P s s ′ a ( R s s ′ a + γ V γ π ( s ′ ) ) V_\gamma^\pi(s) = \sum_{a\in A}\pi(s,a)\sum_{s'\in S}P_{ss'}^a(R_{ss'}^a + \gamma V_{\gamma}^\pi(s')) Vγπ(s)=a∈A∑π(s,a)s′∈S∑Pss′a(Rss′a+γVγπ(s′))
上式被称为Bellman等式。正是由于模型已知,则P(状态转移概率)和R(奖赏概率)已知,从而进行全概率展开。有了状态值函数,直接计算状态-动作值函数:
{ Q T π ( s , a ) = ∑ s ′ ∈ S P s s ′ a ( 1 T R s s ′ a + T − 1 T V T − 1 π ( s ′ ) ) Q γ π ( s , a ) = ∑ s ′ ∈ S P s s ′ a ( R s s ′ a + γ V γ π ( s ′ ) ) \begin{cases} Q_T^\pi(s,a) = \sum_{s'\in S}P_{ss'}^a(\frac{1}{T}R_{ss'}^a+\frac{T-1}{T}V_{T-1}^{\pi}(s')) \\ \\ Q_\gamma^\pi(s,a) = \sum_{s'\in S}P_{ss'}^a(R_{ss'}^a+\gamma V_\gamma^\pi(s')) \end{cases} ⎩⎪⎨⎪⎧QTπ(s,a)=∑s′∈SPss′a(T1Rss′a+TT−1VT−1π(s′))Qγπ(s,a)=∑s′∈SPss′a(Rss′a+γVγπ(s′))
2.2 policy 改进
我们希望policy能最大化累计奖赏:
π ∗ = arg max π ∑ s ∈ S V π ( s ) \pi^*=\text{arg}\max\limits_\pi\sum_{s\in S}V^\pi(s) π∗=argπmaxs∈S∑Vπ(s)
由于最优值函数的累积奖赏已达最大,因此可对Bellman等式做一个改动,即将对动作的求和改为取最优,那么就有:
V ∗ ( s ) = max a ∈ A Q π ∗ ( s , a ) V^*(s) = \max\limits_{a \in A}Q^{\pi^*}(s,a) V∗(s)=a∈AmaxQπ∗(s,a)
这被称为最优Bellman等式。并且可以证明,这种对策略的改进是单调递增(或不减)的。
基于bellman等式的value function估计和策略更新:
- 步骤:开始时采用随机策略 π \pi π,迭代估计 V π ( s ) V_\pi(s) Vπ(s),再通过收敛的 V π ( s ) V_\pi(s) Vπ(s)更新 π \pi π
但是可以证明,策略迭代算法中,策略改进与值的改进是一致的,即我们可以省略改进 π \pi π的过程,得到值迭代算法。
3. Monte Carlo methods 蒙特卡洛法
model-free模型,在没有模型的情况下,策略迭代算法遇到的问题是策略无法评估,由于无法进行全概率展开。另一方面,策略迭代算法估计的函数是状态值函数 V ( s ) V(s) V(s),状态-动作值函数通过该函数获得,现在由于其无法估计,我们直接将估计对象改为状态-动作值 Q ( s , a ) Q(s,a) Q(s,a)
此外,由于模型未知,机器只能从起始状态开始探索,逐渐发现各状态并估计 Q ( s , t ) Q(s,t) Q(s,t)
假设我们使用某种策略进行采样,执行该策略T步,得到一条轨迹(也叫episode):
< s 0 , a 0 , r 1 , s 1 , a 1 , r 2 , . . . , s T − 1 , a T − 1 , r T , s T >
然后对该轨迹中每一对state-action,记录其后的累积奖赏R,作为这一对state-action的一次采样。那么当有多条轨迹后,我们可以对每一对state-action做平均,得到对Q(s,a)的估计,即:
Q ( S t , A t ) = Q ( S t , A t ) × count ( S t , A t ) + R count ( S t , A t ) + 1 count ( S t , A t ) = count ( S t , A t ) + 1 Q(S_t,A_t)= \frac{Q(S_t,A_t)\times \text{count}(S_t,A_t)+R}{\text{count}(S_t,A_t)+1}\\ \text{count}(S_t,A_t)=\text{count}(S_t,A_t)+1 Q(St,At)=count(St,At)+1Q(St,At)×count(St,At)+Rcount(St,At)=count(St,At)+1
式中的均值采用增量式方法计算。
由于一次episode可能会出现多次状态 s s s,所以可以分为:
- Every-visit MC: 用每个episode中所有出现状态 s s s后的return的均值估计
- First-visit MC: 用每个episode中第一次出现状态 s s s产生的return值的均值估计
上述的两种MC方法都会随着遇到状态 s 的次数增长而收敛到 v π ( s ) v_\pi(s) vπ(s)。每个return 都是$ v_\pi(s) $的独立同分布的估计,根据大数定理这些估计值会收敛到期望值。
4. Temporal-Difference methods 时序差分学习
蒙特卡洛算法通过多次尝试(生成多个轨迹)后求平均作为期望累计奖赏的近似。但它求平均时总是要先生成一个episode,再对所有出现的状态-动作对进行更新,即批处理式进行。
而TD模型在每一次出现状态-动作对就更新,即不需要求解累积奖赏R了,仅仅求解瞬时reward值 r r r即可。假设对于状态动作对(s,a),基于t个采样以估计出 Q t π ( s , a ) = 1 t ∑ i = 1 t r i Q_t^\pi(s,a)=\frac{1}{t}\sum_{i=1}^tr_i Qtπ(s,a)=t1∑i=1tri,那么得到第t+1个采样的reward值 r t + 1 r_{t+1} rt+1时,可以有如下更新:
Q t + 1 π ( s , a ) = Q t π ( s , a ) + 1 t + 1 ( r t + 1 − Q t π ( s , a ) ) = Q t π ( s , a ) + α ( r t + 1 − Q t π ( s , a ) ) \begin{aligned} Q_{t+1}^\pi(s,a) &= Q_t^\pi(s,a)+\frac{1}{t+1}(r_{t+1}-Q_t^\pi(s,a)) \\ &= Q_t^\pi(s,a)+\alpha(r_{t+1}-Q_t^\pi(s,a)) \\ \end{aligned} Qt+1π(s,a)=Qtπ(s,a)+t+11(rt+1−Qtπ(s,a))=Qtπ(s,a)+α(rt+1−Qtπ(s,a))
对于 γ \gamma γ折扣累计奖赏为例,可有:
Q π ( s , a ) = ∑ s ′ ∈ S P s s ′ a ( R s s ′ a + γ V π ( s ′ ) ) = ∑ s ′ ∈ S P s s ′ a ( R s s ′ a + γ ∑ a ′ ∈ A π ( s ′ , a ′ ) Q π ( s ′ , a ′ ) ) \begin{aligned} Q^\pi(s,a) &= \sum_{s'\in S}P_{ss'}^a(R_{ss'}^a + \gamma V^\pi(s'))\\ &=\sum_{s'\in S}P_{ss'}^a(R_{ss'}^a + \gamma \sum_{a'\in A}\pi(s',a')Q^\pi(s',a'))\\ \end{aligned} Qπ(s,a)=s′∈S∑Pss′a(Rss′a+γVπ(s′))=s′∈S∑Pss′a(Rss′a+γa′∈A∑π(s′,a′)Qπ(s′,a′))
通过增量求和有:
Q t + 1 π ( s , a ) = Q t π ( s , a ) + α ( R s s ′ a + γ Q t π ( s ′ , a ′ ) − Q t π ( s , a ) ) Q_{t+1}^\pi(s,a)=Q_t^\pi(s,a)+\alpha(R_{ss'}^a+\gamma Q_t^\pi(s',a')-Q_t^\pi(s,a)) Qt+1π(s,a)=Qtπ(s,a)+α(Rss′a+γQtπ(s′,a′)−Qtπ(s,a))
五、时序模型:RNN&LSTM&Attention
什么是sequence数据?指在不同时间点收集到的数据,反映某一事物随时间变化的状态或程度。
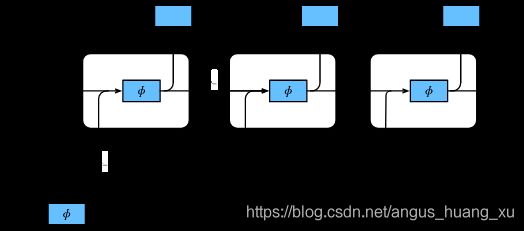
1. RNN循环神经网络
RNN的经典结构如下图所示:
可见一个隐藏的RNN单元接收两个 i n p u t : X t , H t − 1 input:X_t,H_{t-1} input:Xt,Ht−1,输出两个 o u t p u t : H t , Y t output:H_t,Y_t output:Ht,Yt,公式如下:
H t = ϕ ( W x h X t + W h h H t − 1 + b h ) Y t = σ ( W h y H t + b y ) H_t = \phi(W_{xh}X_t + W_{hh}H_{t-1}+b_h)\\ Y_t = \sigma(W_{hy}H_t+b_y) Ht=ϕ(WxhXt+WhhHt−1+bh)Yt=σ(WhyHt+by)
它可以有很多形式,例如:
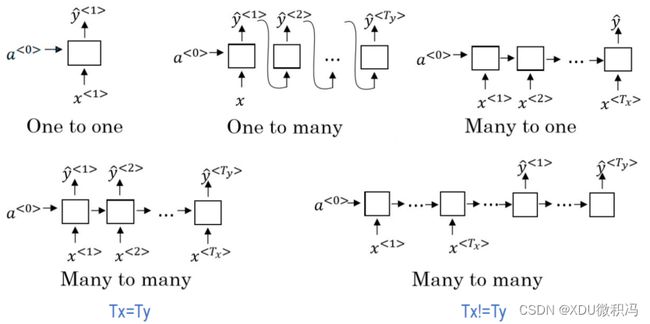
也可以是多层的、双向的。
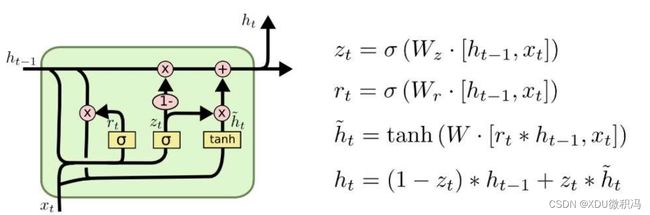
2. LSTM
与RNN不同,从输入上,将接收 C , H , X C,H,X C,H,X,并最终输出 C ∗ , H ∗ , Y C^*,H^*,Y C∗,H∗,Y.
一个普通的LSTM结构如下图所示(图中标识了一些操作的作用):
总的公式如下:
1. 遗忘门: f t = σ ( W f ⋅ [ H t − 1 , X t ] + b f ) 2. 输入门: i t = σ ( W i ⋅ [ H t − 1 , X t ] + b i ) 3. 候选值: C ~ t = tanh ( W c ⋅ [ H t − 1 , X t ] + b C ) 4. 更新C: C t = f t ⋅ C t − 1 + i t ⋅ C ~ t 5. 输出门: o t = σ ( W o ⋅ [ H t − 1 , X t ] + b o ) 6. 更新H: H t = o t ⋅ tanh ( C t ) \begin{aligned} & \text{1. 遗忘门:} f_t=\sigma(W_f\cdot [H_{t-1},X_t]+b_f) \\ & \text{2. 输入门:} i_t=\sigma(W_i\cdot [H_{t-1},X_t]+b_i) \\ & \text{3. 候选值:} \tilde C_t=\tanh(W_c\cdot [H_{t-1},X_t]+b_C)\\ & \text{4. 更新C:} C_t=f_t\cdot C_{t-1} + i_t \cdot \tilde C_t \\ & \text{5. 输出门:} o_t = \sigma(W_o\cdot [H_{t-1},X_t]+b_o) \\ & \text{6. 更新H:} H_t = o_t \cdot \tanh(C_t) \end{aligned} 1. 遗忘门:ft=σ(Wf⋅[Ht−1,Xt]+bf)2. 输入门:it=σ(Wi⋅[Ht−1,Xt]+bi)3. 候选值:C~t=tanh(Wc⋅[Ht−1,Xt]+bC)4. 更新C:Ct=ft⋅Ct−1+it⋅C~t5. 输出门:ot=σ(Wo⋅[Ht−1,Xt]+bo)6. 更新H:Ht=ot⋅tanh(Ct)
- 为什么我们的三个门不使用input中的 C t − 1 C_{t-1} Ct−1?
当然可以用,Peephole就是如下定义三个门的:
遗忘门: f t = σ ( W f ⋅ [ C t − 1 , H t − 1 , X t ] + b f ) 输入门: i t = σ ( W i ⋅ [ C t − 1 , H t − 1 , X t ] + b i ) 输出门: o t = σ ( W o ⋅ [ C t − 1 , H t − 1 , X t ] + b o ) \begin{aligned} & \text{遗忘门:} f_t=\sigma(W_f\cdot [C_{t-1},H_{t-1},X_t]+b_f) \\ & \text{输入门:} i_t=\sigma(W_i\cdot [C_{t-1},H_{t-1},X_t]+b_i) \\ & \text{输出门:} o_t = \sigma(W_o\cdot [C_{t-1},H_{t-1},X_t]+b_o) \\ \end{aligned} 遗忘门:ft=σ(Wf⋅[Ct−1,Ht−1,Xt]+bf)输入门:it=σ(Wi⋅[Ct−1,Ht−1,Xt]+bi)输出门:ot=σ(Wo⋅[Ct−1,Ht−1,Xt]+bo)
- 虽然遗忘门和输入门使用sigmoid把值设置在0-1之间,但并不满足相加为1的归一条件
可以不要输入门!
更新C: C t = f t ⋅ C t − 1 + ( 1 − f t ) ⋅ C ~ t \text{更新C:} C_t=f_t\cdot C_{t-1} + (1-f_t) \cdot \tilde C_t \\ 更新C:Ct=ft⋅Ct−1+(1−ft)⋅C~t
- 输入门和遗忘门能不能结合在一起呢? C t C_t Ct和 H t H_t Ht能不能结合呢?
3. RNN条件生成模型
什么是条件生成?简单来说就是生成一个前后关联的序列。比如下图就解释了条件生成的步骤:
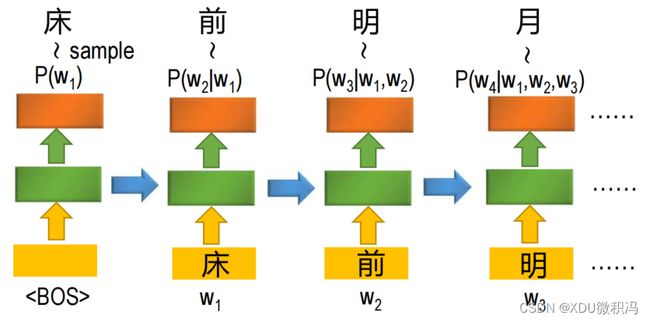
3.1 seq2seq
seq2seq模型使用较为广泛,就不再介绍了。例如,在做机器翻译时可以将中文输入到一个RNN(被称为encoder)中,然后取最后一个时间点的输出,这个输出可以认为包含了整个中文句子的信息,然后将输出的这个向量输入到另一个RNN(被称为decoder)中的每个时间点,使这个RNN来输出对应的英文翻译结果。
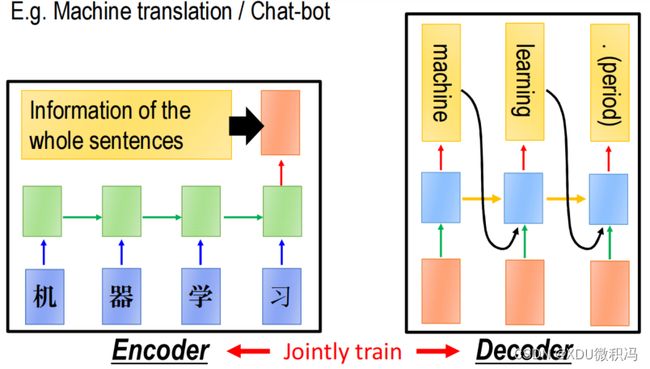
Encoder
-
Hidden state:RNN模块,故为: h t = f ( h t − 1 , x t ) h_t = f(h_{t-1},x_t) ht=f(ht−1,xt)(式子(46))
-
语义(上下文向量):可以指要最后一个Hidden state的输出,当然也可以看所有的hidden state
C = q ( h 1 , h 2 , . . . , h N ) C = q(h_1,h_2,...,h_N) C=q(h1,h2,...,hN) or h N h_N hN
Decoder
- y t = argmax P ( y t ) = ∏ t = 1 T p ( y t ∣ y 1 , . . . , y t − 1 , C ) y_t = \text{argmax}P(y_t) = \prod_{t=1}^Tp(y_t|y_1,...,y_{t-1},C) yt=argmaxP(yt)=∏t=1Tp(yt∣y1,...,yt−1,C)
有3种结构:
1.把上下文向量C当作decoder的 h 0 ′ h'_0 h0′:
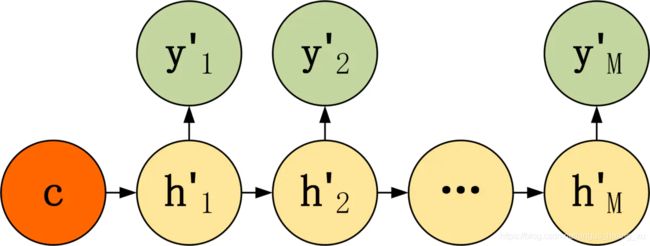
h t ′ = σ ( W h t − 1 ′ + b ) y t = σ ( V h t ′ + b y ) h_t'= \sigma(Wh_{t-1}^{'}+b)\\ y_t = \sigma(Vh'_t+b_y) ht′=σ(Wht−1′+b)yt=σ(Vht′+by)
2.把上下文向量C当作decoder每个神经元的输入:
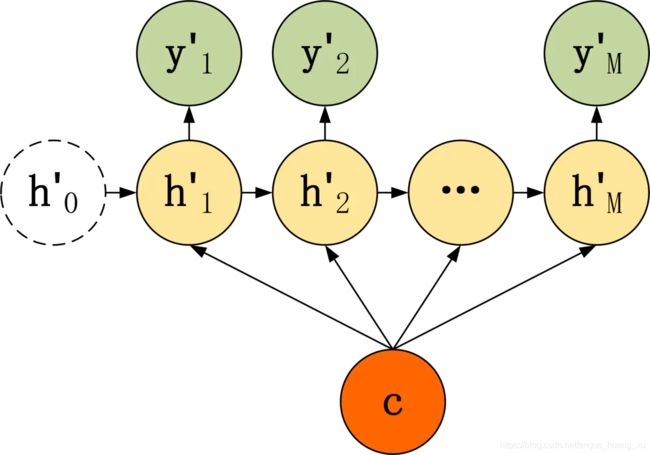
h t ′ = σ ( W 1 C + W 2 h t − 1 ′ + b h ) y t ′ = σ ( V h t ′ + b y ) \begin{aligned} & h'_t=\sigma(W_1C+W_2h'_{t-1}+b_h)\\ & y'_t = \sigma(Vh'_t + b_y) \end{aligned} ht′=σ(W1C+W2ht−1′+bh)yt′=σ(Vht′+by)
3.将上下文向量C和前一层的输出都作为输入:
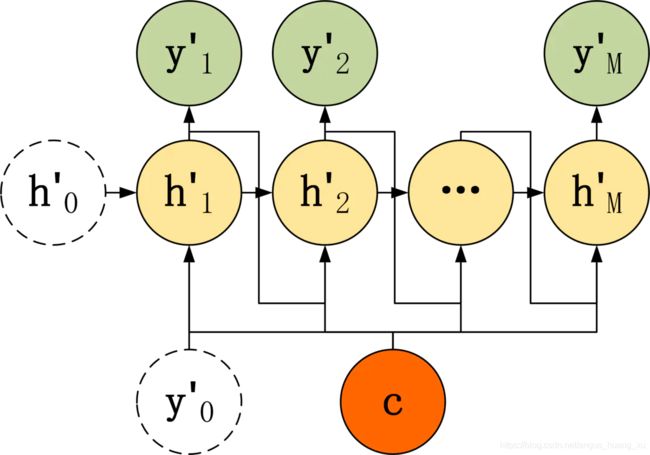
h t ′ = σ ( W 1 C + W 2 h t − 1 ′ + W 3 y t − 1 ′ + b h ) y t ′ = σ ( V h t ′ + b y ) \begin{aligned} & h'_t=\sigma(W_1C+W_2h'_{t-1}+W_3y'_{t-1}+b_h)\\ & y'_t = \sigma(Vh'_t+b_y) \end{aligned} ht′=σ(W1C+W2ht−1′+W3yt−1′+bh)yt′=σ(Vht′+by)
seq2seq结构的问题:
- 所有输入集 X \pmb{X} XXX被压缩为一个上下文向量C,且C与最后几个隐藏状态关系较大,当时间序列很长会失效;
- 编码器按顺序接收输入,所以C包含顺序信息,使得Decoder遵循该顺序输出,但希望的可能不是这样(例如倒装句翻译)
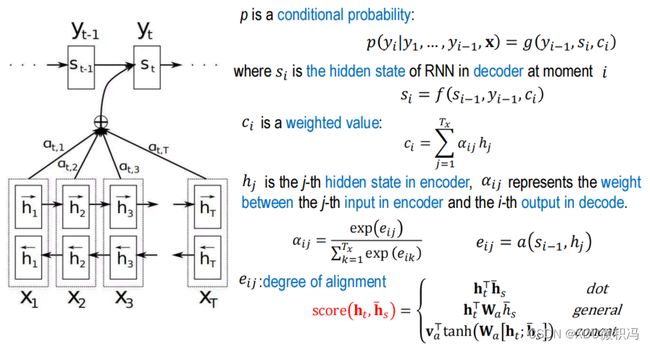
3.2 Attention
Attention在Decoder上的结构与上述的第三种情况相似,即
y t ′ = g ( y t − 1 ′ , h i − 1 , C i ) y'_t=g(y'_{t-1},h_{i-1},C_i) yt′=g(yt−1′,hi−1,Ci)
但是在实现上有所不同,比如:
- 上下文向量将不再是唯一的C,而是与位置相关的 C i C_i Ci
- C i C_i Ci是Encoder所有hidden state的加权求和,权重用相似性表示
为避免混淆,下图将Encoder的hidden state记为 h i h_i hi,把Decoder的hidden state记作 s i s_i si:
六、Emotion & Facial Expression
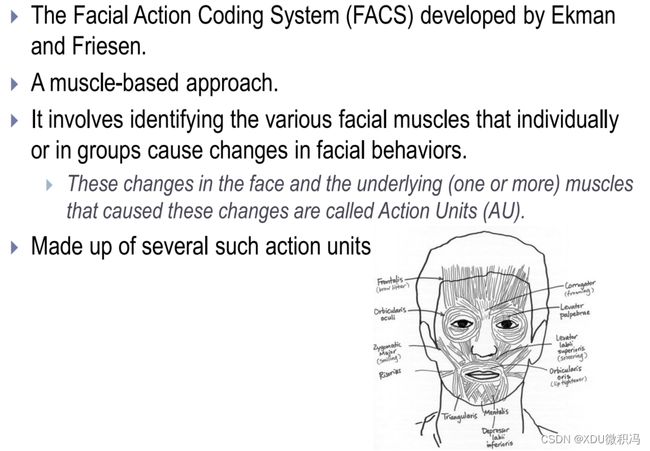
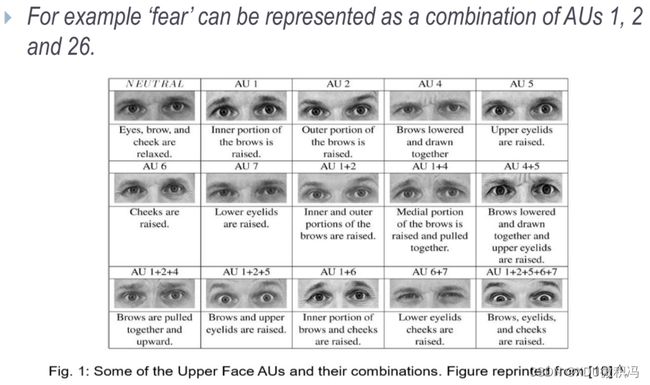
1. 面部编码/参数化
2. 面部表情识别
-
Kanade-Lucas-Tomasi tracker
-
Ratio Template Tracker:用16个区域、23个箭头确定人脸。
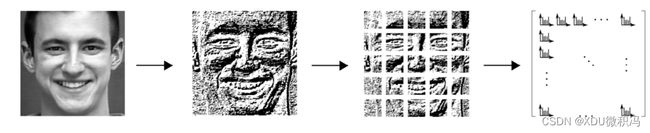
3. feature extraction
- 基于几何的方法:ASM、AAM、SIFT(尺度不变特征变换)、特征点跟踪
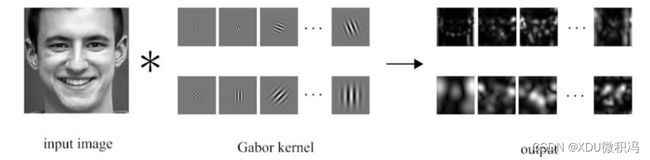
- 基于外观的方法:LBP(划分子块,每块计算二进制代码的直方图)、Gabor-wavelet(维数太大)、HoG
4. 分类
- 神经网络
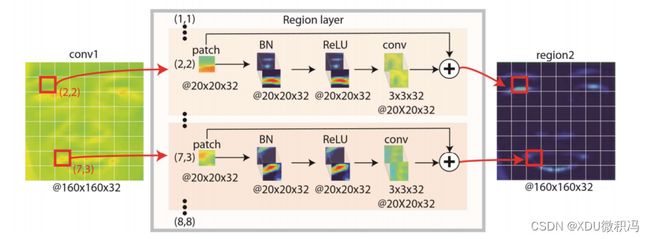
- DRML(深度区域和多标签学习)
还有很多,但不用记住太多方法,只要知道表情识别是什么,怎样特征提取(具体方法不要求)。
教师:梁雪峰教授
written by XDU 微积冯