数据分析之缺失值填充（重点讲解多重插值法Miceforest）

数据分析之缺失值填充（重点讲解多重插值法Miceforest）

数据分析的第一步——数据预处理，不可缺失的一步。为了得到更好的结果，选择合适的数据处理方法是非常重要的！
数据预处理之缺失值填充
在大数据样本时，缺失少量的数据时，可以选择直接剔除，也可以按照某种方法进行填充。在小数据样本时，只能选择填充缺失值。
缺失值填充的常用方法：均值填充、众数填充、多重插值法（更适用于多模态数据，例如医学数据）、K近邻填充、回归/分类预测填充（线性回归、非线性回归、随机森林等多种机器学习方法，或神经网络）。常用且简单的方法就是均值填充、众数填充、多重插值法填充。回归/分类预测填充法就是使用未缺失的数据预测缺失数据，增大了工作量。
Python实现缺失值的填充：
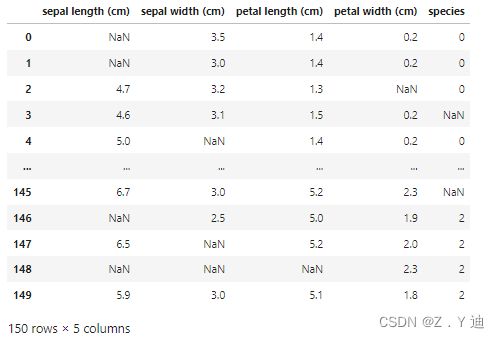
先制作一个有缺失值的数据集，如下：

import miceforest as mf
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris

iris_data = load_iris()
iris = pd.concat(load_iris(as_frame=True,return_X_y=True),axis=1)
iris.rename({"target": "species"}, inplace=True, axis=1)
iris['species'] = iris['species'].astype('category')
iris_amp = mf.ampute_data(iris,perc=0.25,random_state=1991)   #先做一个有缺失值的数据

print(iris_amp.isnull().sum())  # 查看缺失值及数量

#sepal length (cm)    37
#sepal width (cm)     37
#petal length (cm)    37
#petal width (cm)     37
#species              37
#dtype: int64

# 看下现在的数据
iris_amp

#使用均值填充缺失值

#使用均值填充缺失值数据
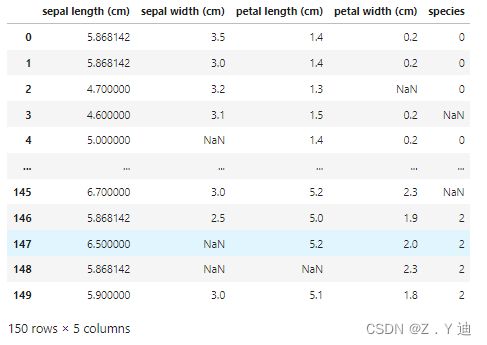
New_iris_amp = iris_amp.fillna(iris_amp.mean())  #当然也可以一列一列的填充  
New_iris_amp

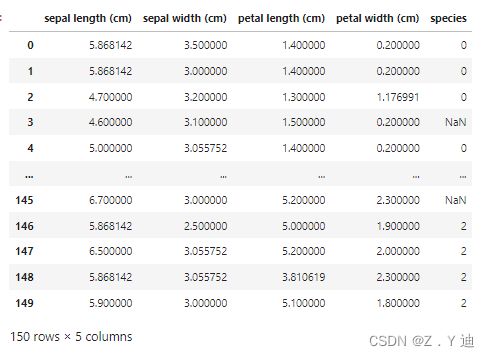
#观察上图，发现species类别这一列并没有填充。iris这个数据集中species是作为标签，是一组分类数据即离散数值。如果取均值可能会出现小数。这里python应该是自动识别它是分类类型变量，没有填充，也是合理的。
我们也可以检查一下填充的缺失值是不是原数据的均值。

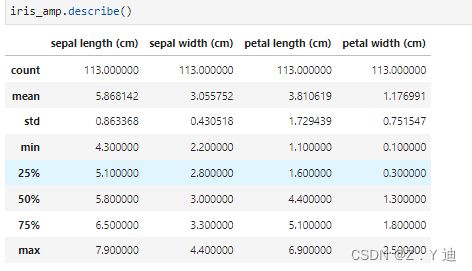
#使用其他值填充缺失值的方法和均值一样，自行选择。
上述操作是整个数据所有列按照均值填充的。有的时候，你不想每列都使用均值填充，那就一列一列的填充或多列一起填充(顺便介绍下fillna函数)，演示如下：
#fillna()函数

#只对某一列进行缺失值的填充
iris_amp['sepal length (cm)'].fillna(value=iris_amp['sepal length (cm)'].mean(),inplace=True)
iris_amp

#现实中我们用的是自己的数据，当然需要先将数据导入到Python中，填充后导出。这里顺便把这个操作写进来
#导出方法
New_iris_amp.to_excel(r'E:\CSDN\New_iris_amp.xlsx')
#导入方法
Data = pd.read_excel(r'E:\CSDN\New_iris_amp.xlsx')
Data

本文重点介绍：多重插值法（miceforest）
miceforest：使用 lightgbm 进行快速、高效的内存插补

• 快速：使用 lightgbm 作为后端，并有高效的均值匹配解决方案。
• 内存高效：能够在不复制数据集的情况下执行多重插补。如果数据集可以放入内存，则可以（可能）进行估算。
• 灵活：可以处理 pandas DataFrames 和 numpy 数组。插补过程可以完全定制。可以自动处理分类数据。
• 用于生产：使用的内核可以被保存（推荐使用 dill 包）并估算新的、看不见的数据集。输入新数据通常比在新mice程序中包含新数据快几个数量级。即使没有缺失值，也可以根据内核数据集构建插补模型。新数据也可以就地估算。
  网站：miceforest官网
  python安装命令（pip 或 conda 选一种）：

 pip install miceforest
 pip install git+https://github.com/AnotherSamWilson/miceforest.git
 conda install -c conda-forge miceforest

本文介绍的版本是2022年4月15日最新发行的，和之前有所不同。

• 新的主类 ( ImputationKernel, ImputedData) 替换 ( KernelDataSet, MultipleImputedKernel, ImputedDataSet, MultipleImputedDataSet)。
  现在可以在适当的位置引用和估算数据。这节省了大量内存分配并且速度更快。
• 现在可以就地完成数据。这允许在任何给定时间仅在内存中存储一​​个数据集副本，即使执行多重插补也是如此。
• mean_match_subset参数已替换data_subset. 为此子集用于构建模型的数据以及候选数据。
• 数据复制时间和存储位置的更多性能改进。
• 原始数据现在作为原始数据存储。可以处理 pandas DataFrame和 numpy ndarray。
  案例

#如果只想创建单个插补数据集，将datasets设置为1
kds = mf.ImputationKernel(
    iris_amp,
    datasets=1,
    save_all_iterations=True,
    random_state=1991
)
#查看下kds
print(kds)
#              Class: ImputationKernel
#          Datasets: 1
#         Iterations: 0
#  Imputed Variables: 4
save_all_iterations: True
#设置mice算法迭代3次
kds.mice(3)

我们通常不想只估算单个数据集。在统计学中，多重插补是一个过程，通过该过程可以通过创建多个不同的插补数据集来检查由缺失值引起的不确定性/其他影响。ImputationKernel可以包含任意数量的不同数据集，所有这些数据集都经历了互斥的插补过程。如下：

# Create kernel. 
kernel = mf.ImputationKernel(
  iris_amp,
  datasets=4,
  save_all_iterations=True,
  random_state=1
)

# Run the MICE algorithm for 2 iterations on each of the datasets
kernel.mice(2)

# Printing the kernel will show you some high level information.
print(kernel)
##               Class: ImputationKernel
##            Datasets: 4
##          Iterations: 2
##   Imputed Variables: 5
## save_all_iterations: True

#运行mice后，从kernel中获取完整的数据集
completed_dataset = kernel.complete_data(dataset=0,inplace=False)
print(completed_dataset.isnull().sum())

## sepal length (cm)    0
## sepal width (cm)     0
## petal length (cm)    0
## petal width (cm)     0
## species              0
## dtype: int64

使用inplace=False返回已完成数据的副本。由于原始数据已经存储在 中kernel.working_data，您可以设置 inplace=True完成数据而不返回副本

kernel.complete_data(dataset=0, inplace=True)
print(kernel.working_data.isnull().sum(0))
## sepal length (cm)    0
## sepal width (cm)     0
## petal length (cm)    0
## petal width (cm)     0
## species              0
## dtype: int64

控制树的生长

# Run the MICE algorithm for 1 more iteration on the kernel with new parameters
kernel.mice(iterations=1,n_estimators=50)

当然你也会发现iris数据中species种类数据是分类类型，在插补的过程需要更多时间，就因为它是多类的，你可以通过以下方式减少专门针对该列的n_estimators:

# Run the MICE algorithm for 2 more iterations on the kernel 
kernel.mice(iterations=1,variable_parameters={'species': {'n_estimators': 25}},n_estimators=50)

这种方式和上述方式有所不同，但是在这种情况下，指定的任何参数variable_parameters都将优于第一种方式kwargs。

如果你知道你的数据初始的分布的话，这也可以设置
如下，sepal width (cm)是一种泊松分布。

# Create kernel. 
cust_kernel = mf.ImputationKernel(
  iris_amp,
  datasets=1,
  random_state=1
)

cust_kernel.mice(iterations=1, variable_parameters={'sepal width (cm)': {'objective': 'poisson'}})

使用 Gradient Boosted Trees（梯度树）进行插补
初始默认的方式是随机森林

# 创建内核。
kds_gbdt = mf.ImputationKernel(
  iris_amp,
  datasets=1,
  save_all_iterations=True,
  random_state=1991
)

# 我们需要添加一个小的最小 hessian，否则 lightgbm 会报错：
kds_gbdt.mice(iterations=1, boosting='gbdt', min_sum_hessian_in_leaf=0.01) 
# Return the completed kernel data
completed_data = kds_gbdt.complete_data(dataset=0)
#结果如下图

自定义插补过程
可以通过变量大量定制我们的插补程序。通过将命名列表传递给variable_schema，您可以为要估算的每个变量指定预测变量。您还可以 通过传递有效值的字典来指定mean_match_candidates和按变量，变量名作为键。data_subset如果您愿意，您甚至可以替换整个默认均值匹配函数

var_sch = {
    'sepal width (cm)': ['species','petal width (cm)'],
    'petal width (cm)': ['species','sepal length (cm)']
}
var_mmc = {
    'sepal width (cm)': 5,
    'petal width (cm)': 0
}
var_mms = {
  'sepal width (cm)': 50
}

# The mean matching function requires these parameters, even
# if it does not use them.
def mmf(
  mmc,
  model,
  candidate_features,
  bachelor_features,
  candidate_values,
  random_state,
  hashed_seeds
):

    bachelor_preds = model.predict(bachelor_features)
    imp_values = random_state.choice(candidate_values, size=bachelor_preds.shape[0])

    return imp_values

cust_kernel = mf.ImputationKernel(
    iris_amp,
    datasets=3,
    variable_schema=var_sch,
    mean_match_candidates=var_mmc,
    data_subset=var_mms,
    mean_match_function=mmf
)
cust_kernel.mice(1)

使用现有模型估算新数据
多重插补可能需要很长时间。如果您希望使用 MICE 算法估算数据集，但没有时间训练新模型，则可以使用ImputationKernel 对象估算新数据集。该impute_new_data()函数使用收集的随机森林ImputationKernel来执行多重插补，而不在每次迭代时更新随机森林：

from datetime import datetime

# 选取iris_amp中的前15行数据作为新输入的数据
new_data = iris_amp.iloc[range(15)]

start_t = datetime.now()
new_data_imputed = kernel.impute_new_data(new_data=new_data)
print(f"New Data imputed in {(datetime.now() - start_t).total_seconds()} seconds")

也可以在非缺失数据上构建模型

orig_missing_cols = ["sepal length (cm)", "sepal width (cm)"]
new_missing_cols = ["sepal length (cm)", "sepal width (cm)", "species"]

iris_amp2 = iris.copy()
iris_amp2[orig_missing_cols] = mf.ampute_data(
  iris_amp2[orig_missing_cols],
  perc=0.25,
  random_state=1991
)
var_sch = new_missing_cols
cust_kernel = mf.ImputationKernel(
    iris_amp2,
    datasets=1,
    variable_schema=var_sch,
    train_nonmissing=True
)
cust_kernel.mice(1)
iris_amp2_new = iris.iloc[range(10),:].copy()
iris_amp2_new[new_missing_cols] = mf.ampute_data(
  iris_amp2_new[new_missing_cols],
  perc=0.25,
  random_state=1991
)


iris_amp2_new_imp = cust_kernel.impute_new_data(iris_amp2_new)
iris_amp2_new_imp.complete_data(0).isnull().sum()

#sepal length (cm)    0
#sepal width (cm)     0
#petal length (cm)    0
#petal width (cm)     0
#species              0
#dtype: int64

调整参数使插补结果更好
上述了多种方式及其函数，为了使插补的结果更好，应该多次调整参数，选取最好的结果。

多重插补是处理缺失数据的最可靠的方法之一——但它可能需要很长时间。您可以使用多种策略来减少进程运行所需的时间：

• 减少data_subset。默认情况下，每个变量的所有非缺失数据点都用于训练模型并执行均值匹配。这可能导致模型训练最近邻搜索需要很长时间来处理大数据。可以使用 搜索这些点的子集data_subset。
• 将您的数据转换为 numpy 数组。Numpy 数组的索引速度要快得多。虽然尽可能避免了索引开销，但没有办法绕过它。还要考虑转换为float32数据类型，因为它会导致生成的对象占用更少的内存。
• 减少mean_match_candidates。使用默认参数考虑的最大邻居数为 10。但是，对于大型数据集，这仍然是一项昂贵的操作。考虑明确设置mean_match_candidates较低。
• 使用不同的 lightgbm 参数。lightgbm 通常不是问题，但是如果某个变量有大量的类，那么实际生长的最大树数是 (# classes) * (n_estimators)。您可以专门减少大型多类变量的 bagging 分数或 n_estimators，或者通常减少树的生长。
• 使用更快的均值匹配函数。默认均值匹配函数使用 scipy.Spatial.KDtree 算法。如果您认为均值匹配是阻碍因素，那么还有更快的替代方案。

保存和加载内核
可以使用该.save_kernel()方法保存内核，然后使用该utils.load_kernel()函数再次加载。在内部，此过程使用blosc和dill包来执行以下操作：

1、将工作数据转换为 parquet 字节（如果它是 pandas 数据帧）
2、序列化内核
3、压缩这个序列化
4、保存到文件

诊断绘图

截至目前，miceforest有四个可用的诊断图。
插补值的分布
.plot_imputed_distributions()函数

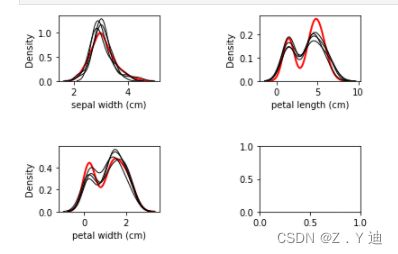
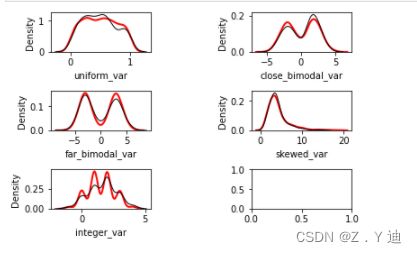
#红线是原始数据，黑线是每个数据集的插补值。
kernel.plot_imputed_distributions(wspace=1,hspace=1)

相关性
.plot_correlations()函数

kernel.plot_correlations(wspace=1,hspace=1)

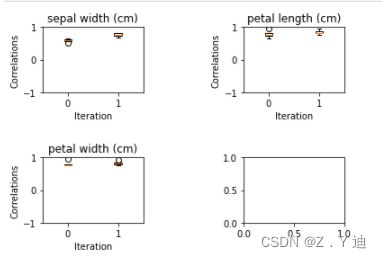
变量的重要性
.plot_feature_importance()

kernel.plot_feature_importance(dataset=0, annot=True,cmap="YlGnBu",vmin=0, vmax=1)

显示的数字是从 lightgbm.Booster.feature_importance()函数返回的。每个方块代表列变量在估算行变量中的重要性

平均值收敛程度
. plot_mean_convergence()
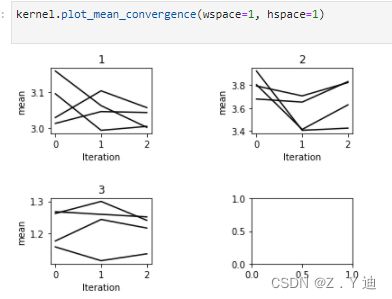
如果我们的数据没有完全随机丢失，我们可能会看到我们的模型需要进行几次迭代才能使插补分布正确。我们可以绘制插补的平均值，看看是否发生了这种情况：

kernel.plot_mean_convergence(wspace=0.3, hspace=0.4)

使用插补数据

#使用插补数据
dataset_0 = kernel.complete_data(0)
dataset_0

MICE算法

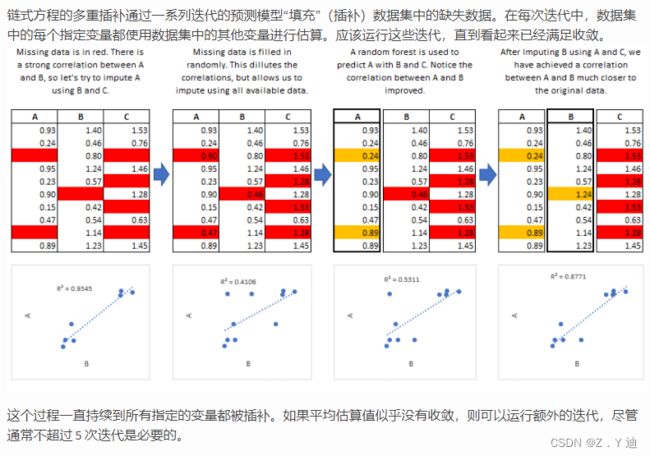
预测均值匹配

均值匹配的影响
这里给出官方的一个代码，可以看看，其实在我们实际应用中，就是加了一个参数而已。直接用就好！（不过可以学习下中seaborn绘图！）

randst = np.random.RandomState(1991)
# random uniform variable
nrws = 1000
uniform_vec = randst.uniform(size=nrws)

def make_bimodal(mean1,mean2,size):
    bimodal_1 = randst.normal(size=nrws, loc=mean1)
    bimodal_2 = randst.normal(size=nrws, loc=mean2)
    bimdvec = []
    for i in range(size):
        bimdvec.append(randst.choice([bimodal_1[i], bimodal_2[i]]))
    return np.array(bimdvec)

# Make 2 Bimodal Variables
close_bimodal_vec = make_bimodal(2,-2,nrws)
far_bimodal_vec = make_bimodal(3,-3,nrws)


# Highly skewed variable correlated with Uniform_Variable
skewed_vec = np.exp(uniform_vec*randst.uniform(size=nrws)*3) + randst.uniform(size=nrws)*3

# Integer variable correlated with Close_Bimodal_Variable and Uniform_Variable
integer_vec = np.round(uniform_vec + close_bimodal_vec/3 + randst.uniform(size=nrws)*2)

# Make a DataFrame
dat = pd.DataFrame(
    {
    'uniform_var':uniform_vec,
    'close_bimodal_var':close_bimodal_vec,
    'far_bimodal_var':far_bimodal_vec,
    'skewed_var':skewed_vec,
    'integer_var':integer_vec
    }
)

# Ampute the data.
ampdat = mf.ampute_data(dat,perc=0.25,random_state=randst)

# Plot the original data
import seaborn as sns
import matplotlib.pyplot as plt
g = sns.PairGrid(dat)
g.map(plt.scatter,s=5)

我们直接使用下这个参数，对比下结果：
参数：mean_match_candidates

kernelmeanmatch = mf.ImputationKernel(ampdat, datasets=1,mean_match_candidates=5)
kernelmodeloutput = mf.ImputationKernel(ampdat, datasets=1,mean_match_candidates=0)

kernelmeanmatch.mice(2)
kernelmodeloutput.mice(2)

kernelmeanmatch.plot_imputed_distributions(wspace=1,hspace=1)

kernelmodeloutput.plot_imputed_distributions(wspace=1,hspace=1)

明显使用均值匹配的方式更好！

总结

通过上述所作的工作可以发现：micsforest在进行插值时，不管是连续变量还是分类变量都能够进行缺失的填充。如果使用传统的均值填充（.fillna()），并不是填充分类变量的缺失值。
从本质上分析多重插值法，其实也是一直利用未缺失数据预测缺失数据。这种方法在医学领域应用比较广泛，在多模态数据中应用广泛。如想了解更详细内容，请查看官网内容。小白学习分享，如有错误请指正，谢谢！