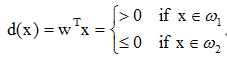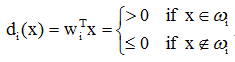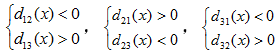判别函数（一）
线性判别函数
用判别函数分类的概念：模式识别系统的主要作用；判别各个模式所属的类别对一个两类问题的判别，就是将模式x划分成ω1和ω2两类。
两类问题的判别函数（以二维模式样本为例）
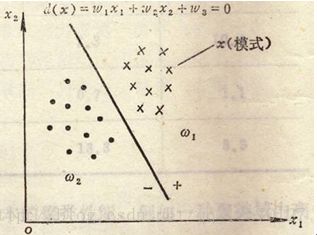
若x是二维模式样本x = (x1 x2)T，用x1和x2作为坐标分量，得到模式的平面图：
这时，若这些分属于ω1和ω2两类的模式可用一个直线方程d(x)=0来划分
d(x) = w1x1 + w2x2 + w3 = 0
其中x1、x2为坐标变量，w1、w2、w3为参数方程，则将一个不知类别的模式代入d(x)，有
- 若d(x) > 0，则 x属于w1.
- 若d(x) < 0，则 x属于w2.
此时，d(x)=0称为判别函数。
用判别函数进行模式分类依赖的两个因素
（1）判别函数的几何性质：线性的和非线性的函数。线性的是一条直线；非线性的可以是曲线、折线等；线性判别函数建立起来比较简单（实际应用较多）；非线性判别函数建立起来比较复杂。
（2）判别函数的系数：判别函数的形式确定后，主要就是确定判别函数的系数问题。只要被研究的模式是可分的，就能用给定的模式样本集来确定判别函数的系数。
一个n维线性判别函数的一般形式：
d(x)也可表示为：d(x) = wTx；其中，x = (x1, x2, …, xn, 1)T称为增广模式向量，w = (w1, w2, …, wn+1)T称为增广权向量。两类情况：判别函数d(x)
多类问题1：
用线性判别函数将属于ωi类的模式与不属于ωi类的模式分开，其判别函数为：
例如对属于w1的模式，应同时满足：d1(x)>0，d2(x)<0，d3(x)<0
不确定区域：若对某一模式区域，di(x)>0的条件超过一个，或全部di(x)<0，i = 1, 2, …, M，则分类失败，这种区域称为不确定区域(IR)。
例：设有一个三类问题，其判别式为：d1(x)= -x1 + x2，d2(x)= x1 + x2 - 5，d3(x)= -x2 + 1则对一个模式x=(6, 5)T，判断其属于哪一类。将x=(6, 5)T代入上述判别函数，得：
假若x=(3, 5)T，则
多类问题2：
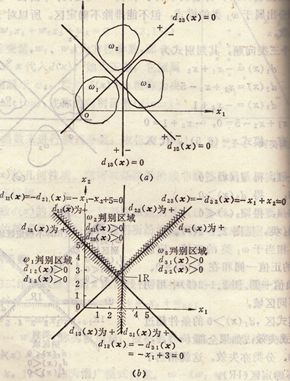
采用每对划分，即ωi/ωj两分法，此时一个判别界面只能分开两种类别，但不能把它与其余所有的界面分开。其判别函数为：
若dij(x)>0，
，则 x属于w1.
重要性质：dij = -dji
图例：对一个三类情况，d12(x)=0仅能分开ω1和ω2类，不能分开ω1和ω3类。要分开M类模式，共需M(M-1)/2个判别函数。不确定区域：若所有dij(x)，找不到 ，dij(x)>0的情况。
例：设有一个三类问题，其判别函数为：d12(x)= -x1 - x2 + 5，d13(x)= -x1 + 3，d23(x)= -x1 + x2若x=(4, 3)T，则：d12(x) = -2，d13(x) = -1，d23(x) = -1有：
若x=(2.8, 2.5)T，则：d12(x) = -0.3，d13(x) = 0.2，d23(x) = -0.3有：
多类问题3：
这是没有不确定区域的ωi/ωj两分法。假若多类情况2中的dij可分解成：dij(x) = di(x) - dj(x) = (wi – wj)Tx，则dij(x)>0相当于di(x)>dj(x)，
，这时不存在不确定区域。此时，对M类情况应有M个判别函数：
，i, j = 1,2,…,M，则 ，也可写成，若di(x)=max{dk(x), k=1,2,…,M}，则 x属于w1类。
该分类的特点是把M类情况分成M-1个两类问题。
例：设有一个三类问题的模式分类器，其判别函数为：d1(x)= -x1 + x2，d2(x)= x1 + x2 - 1，d3(x)= -x2
属于ω1类的区域应满足d1(x)>d2(x)且d1(x)>d3(x)，ω1类的判别界面为：
小结：线性可分模式分类若可用任一个线性函数来划分，则这些模式就称为线性可分的，否则就是非线性可分的。一旦线性函数的系数wk被确定，这些函数就可用作模式分类的基础。
对于M类模式的分类，多类情况1需要M个判别函数，而多类情况2需要M*(M-1)/2个判别函数，当M较大时，后者需要更多的判别式（这是多类情况2的一个缺点）。采用多类情况1时，每一个判别函数都要把一种类别的模式与其余M-1种类别的模式分开，而不是将一种类别的模式仅与另一种类别的模式分开。由于一种模式的分布要比M-1种模式的分布更为聚集，因此多类情况2对模式是线性可分的可能性比多类情况1更大一些（这是多类情况2的一个优点）