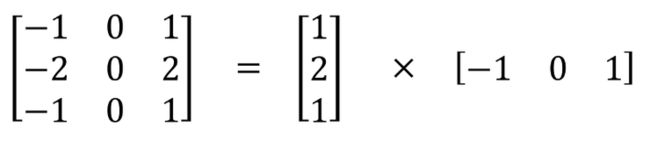深度学习中的常用八种卷积运算简介

参考资料：https://towardsdatascience.com/a-comprehensive-introduction-to-different-types-of-convolutions-in-deep-learning-669281e58215

本文的内容包括：

1. 卷积 VS 互相关(Convolution v.s. Cross-correlation)

2. 常规卷积（单通道版，多通道版）(Convolution  (single channel version, multi-channel version))

3.3D 卷积(3D Convolution)

4. 1x1 卷积(1 x 1 Convolution)

5. 转置卷积（反卷积）(Transposed Convolution (Deconvolution))

6. 空洞卷积（扩张卷积）(Dilated Convolution (Atrous Convolution))

7. 可分离卷积（空间可分离卷积，深度可分离卷积）(Separable Convolution (Spatially Separable Convolution, Depthwise Convolution))

8. 扁平化卷积(Flattened Convolution)

9. 分组卷积(Grouped Convolution)

 

1. 卷积 VS 互相关

    对于一个核，如果核和图像直接相乘，那么就是互相关操作；如果核顺时针旋转180度之后，然后再和图像相乘，那么就是卷积操作。 如果核的值是对称的，那么卷积操作和互相关操作是一样的。在神经网络中，其实我们表面一看，核在和特征图相乘的时候，并没有进行180度旋转，但为什么还是称为卷积运算呢？一种理解是：神经网络在学习的过程中，已经使得核上的值旋转过，省出了旋转这一部分。我的理解是：称互相关或者卷积操作都是没错的，就看你怎么强制性解释吧。

 

2. 深度学习中的卷积

     单通道卷积：特征图通道为1，卷积核通道为1

    多通道卷积：特征图通道大于1，卷积核通道大于1

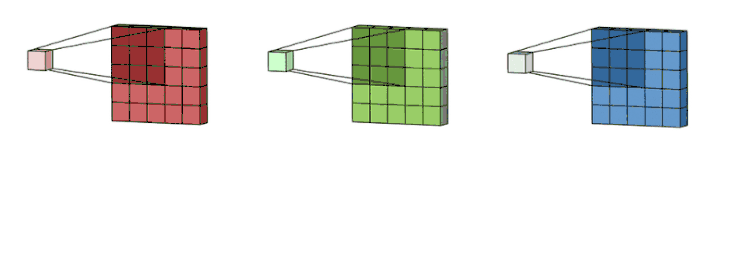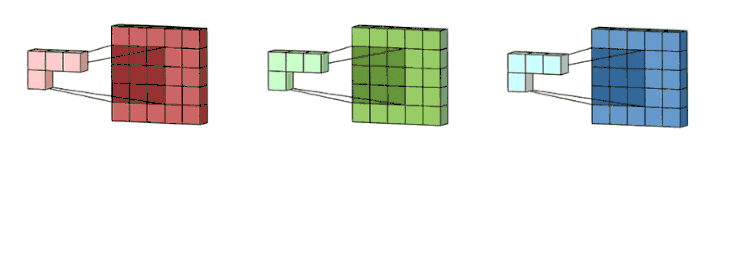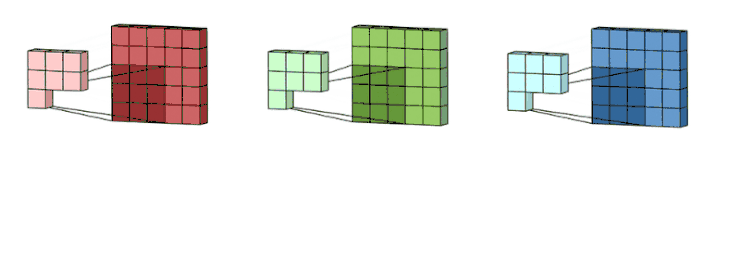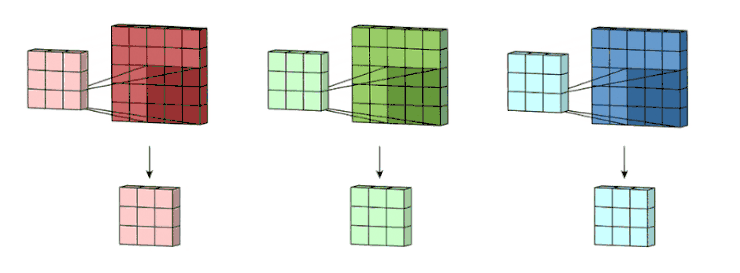
    比如下图中，是3通道5*5大小的图片和3个卷积核大小为3*3进行运算。每个卷积核和一个特征图做运算，各输出一个3*3大小的特征图

      将上面所得到的三个3*3大小的特征图进行相加，得到一个输出（一个3*3大小的特征图）

 

3.3D 卷积

    下图为：一个3*3*3的卷积核在立方体上沿着宽、高以及通道进行卷积（二维卷积只有宽高方向）。看到3D卷积，我们很容易联想到多通道卷积，那么它们两个之间有什么区别：对于多通道卷积，每个通道所对应的卷积是不一样的，而3D卷积，在三维特征上有共享机制（它会在三个维度上面滑动计算）。3D 卷积可以描述 3D 空间中目标的空间关系。对于一些应用来说，这种 3D 关系很重要，例如在 CT 和 MRI 等生物医学图像的 3D 分割/重建中以及视频处理。

     优点：可以充分利用3维之间的关系

     缺点：计算量大，硬件不容易支持

 

4. 1x1 卷积

     将常规卷积（比如3*3的卷积）的长和宽都换成1，则就成了1*1卷积运算，1*1卷积运算就是常规卷积的一个特例。

     常用地方：1.减少中间特征图的维度，以便减少整个模型的计算量；2.对于前面用了深度可分离卷积，后面接这个，是用来增强通道之间的关系

 

5. 转置卷积（反卷积）

     我们可以直接使用卷积来实现转置卷积。例如在下图中，我们选择在 2 x 2 的输入特征图上做转置卷积：其卷积核为 3 x 3，卷积步长为 1，填充为2 。那么上采样的输出大小为 4 x 4。

 

     在2x2的输入特征图中，插入空格，然后选择卷积核为 3 x 3，卷积步长为 1，填充为 2，那么得出的输出大小为 5 x 5。

    上面的结果演示都比较具体，接下来，我们从理论上分析为什么反卷积被称为转置卷积更恰当。

     第一步：将input（4*4的维度）  reshape成16*1的维度，之后将卷积核转换为一个稀疏矩阵 (4 x 16)，接着将两者进行运算，得到一个4*1维度的数组，最后reshape成2*2的特征图

    第二步：将上面的操作进行转置操作（这个就是为什么，反卷积被称为转置卷积更恰当），可以得到下图的计算过程，这个也是我们所需要的

  反卷积会产生一些问题，可参考我以前的博客：反卷积(Deconvolution)与棋盘效应(Checkerboard Artifacts)

 

6. 空洞卷积（扩张卷积）

    直观上，空洞卷积是通过在卷积核部分之间插入空间（这个值一般为0）让卷积核「膨胀」。这个增加的参数 l（空洞率）表明了我们想要将卷积核放宽到多大。下图显示了当 l-1,2,4 时的卷积核大小。利用空洞卷积的好处：在不增加计算量的前提，增加感受野。

 

7. 可分离卷积（空间可分离卷积，深度可分离卷积）

    可分离卷积（空间可分离卷积，深度可分离卷积）都是可以用来减少计算量的。

    空间可分离卷积：将卷积分解为两项单独的操作。下图中，一个卷积核为 3x3 的 Sobel 卷积核拆分成了一个 3x1 卷积核和一个 1x3 卷积核。

    因此在神经网络中，我们可以将3x3的卷积核拆成两部分：

    深度可分离卷积：在卷积计算上，通道之间的计算没有任何关系，是自己对应通道计算自己的（如果计算完之后，不同通道之间特征图相加的话，就变成了常规卷积运算）。

 

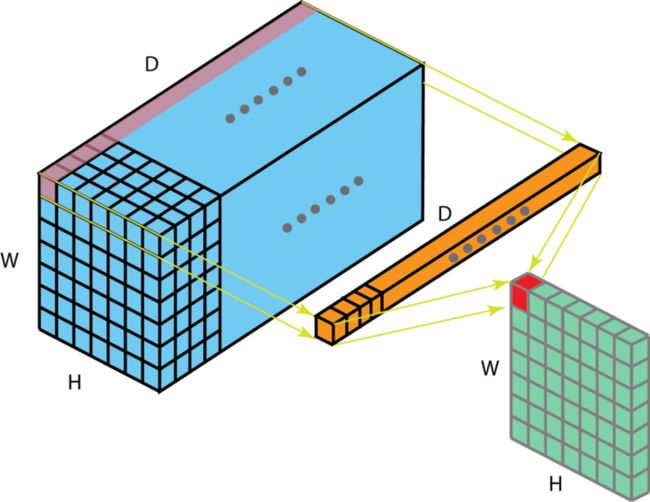
8.扁平化卷积

    扁平化卷积就是空间可分离卷积的特列，只不过是一个3D卷积被分成了三部分。

 

9.分组卷积

    一个完整的卷积组，被分成了两部分，分别来计算输入特征图的各一半，最后将两个输出拼成一个输出。其实，分组卷积最早是出现在AlexNet 文章里面，当初由于显存不够，作者才这样操作的，现在一般是很少用的。