学习周报2
目录
Introduction
Regression-Case Study
Basic Concept
Gradient Descent
Classification
Introduction
Supervised Learning(监督学习)
Supervised learning 需要大量的training data,这些training data告诉我们说,一个我们要找的function,它的input和output之间有什么样的关系
Regression(回归)
通过regression找到的function,它的输出是一个scalar数值
Classification(分类)
model(function set) 选择模型
Semi-supervised Learning(半监督学习)
举例:如果想要做一个区分猫和狗的function,手上有少量的labeled data,它们标注了图片上哪只是猫哪只是狗;同时又有大量的unlabeled data,它们仅仅只有猫和狗的图片,但没有标注去告诉机器哪只是猫哪只是狗.
Transfer Learning(迁移学习)
假设一样我们要做猫和狗的分类问题.我们也一样只有少量的有labeled的data;但是我们现在有大量的不相干的data(不是猫和狗的图片,而是一些其他不相干的图片),在这些大量的data里面,它可能有label也可能没有label
Transfer Learning要解决的问题是,这一堆不相干的data可以对结果带来什么样的帮助。
Unsupervised Learning(无监督学习)
区别于supervised learning,unsupervised learning希望机器学到无师自通,在完全没有任何label的情况下,机器到底能学到什么样的知识。
Structured Learning(结构化学习)
在structured Learning里,我们要机器输出的是,一个有结构性的东西,比如机器翻译、人脸识别。
Reinforcement Learning(强化学习)
我们没有告诉机器正确的答案是什么,机器最终得到的只有一个分数,就是它做的好还是不好,但他不知道自己到底哪里做的不好。
Regression-Case Study
Machine learning的三个步骤:
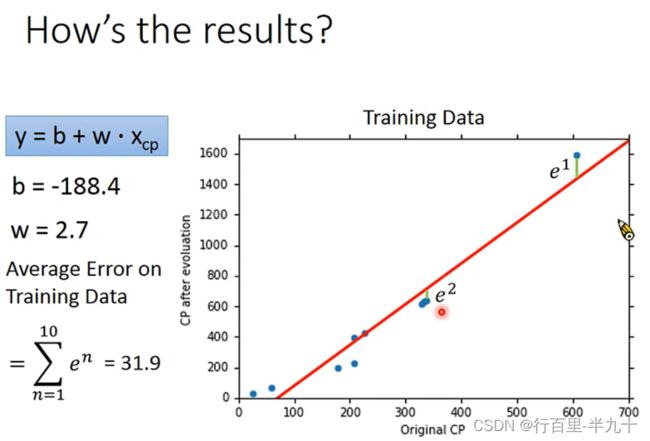
定义一个Model
Goodness of Function
颜色越偏红色代表Loss的数值越大,这个function的表现越不好,越偏蓝色代表Loss的数值越小,这个function的表现越好
Loss function实际上是在衡量一组参数的好坏
Pick the Best Function
Gradient Descent
只要L(f)是可微分的,gradient descent都可以拿来处理这个f,找到表现比较好的parameters
单个参数的问题,可以使用穷举法,但是效率低
两个参数的问题
- 首先,随机选取两个初始值
- 然后分别计算( w0 , b0 )这个点上,L对w和b的偏微分
- 不断迭代找到极小值点
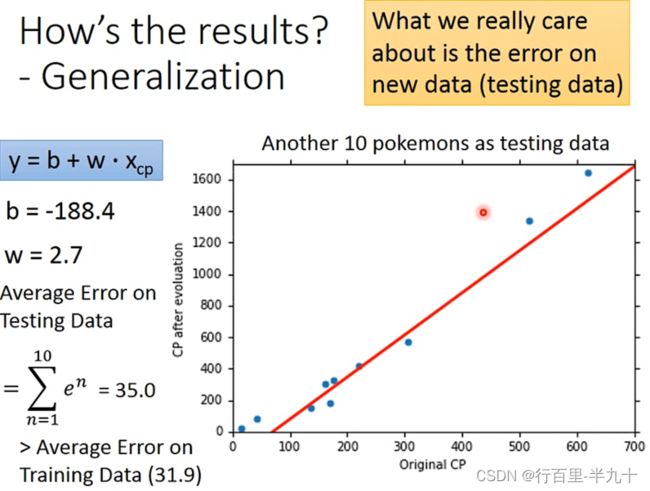
training data里得到的误差一般是要比testing data要小,这也符合常识
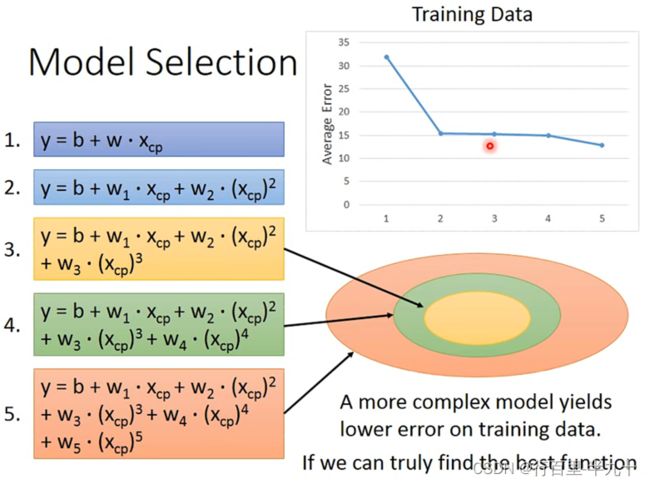
Selecting another model
随着Xcp的高次项的增加,对应的average error会不断地减小
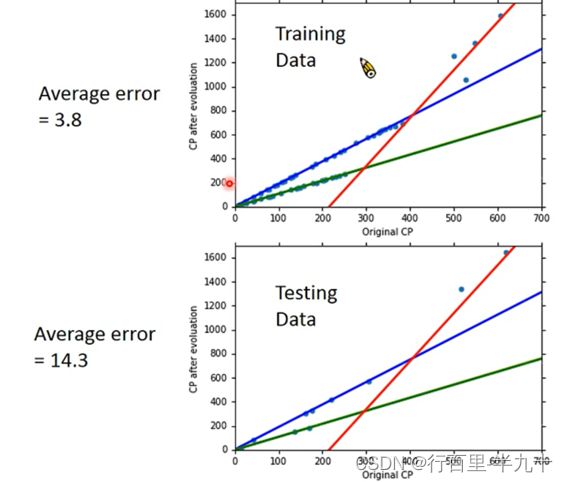
在training data上,model越复杂,error就会越低;但是在testing data上,model复杂到一定程度之后,error非但不会减小,反而会暴增,通常被称为overfitting过拟合。
因此model不是越复杂越好,而是选择一个最适合的mode。
Redesign the model
我们需要进一步考虑其他参数的影响,比如物种
我们需要根据不同的物种,设计不同的linear model
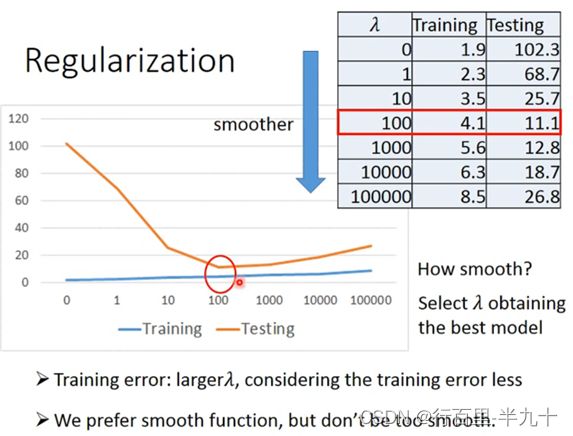
Regularization
regularization可以使曲线变得更加smooth,training data上的error变大,但是 testing data上的error变小,可以解决过拟合的问题。
regularization则是在原来的loss function的基础上加上了一项,就是把这个model里面所有的wi的平方和用λ加权。
当λ从0到100变大的时候,training error不断变大,testing error反而不断变小;但是当λ太大的时候(>100),在testing data上的error就会越来越大。
所以应该选择合适的λ值。
Basic Concept
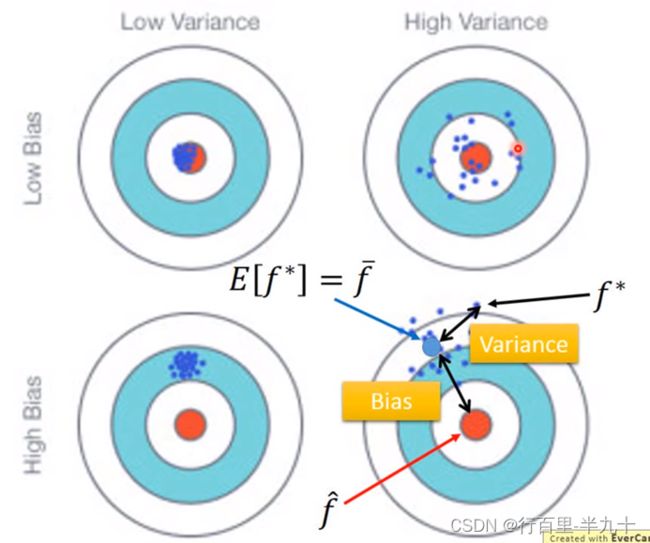
Bias and Variance of Estimator
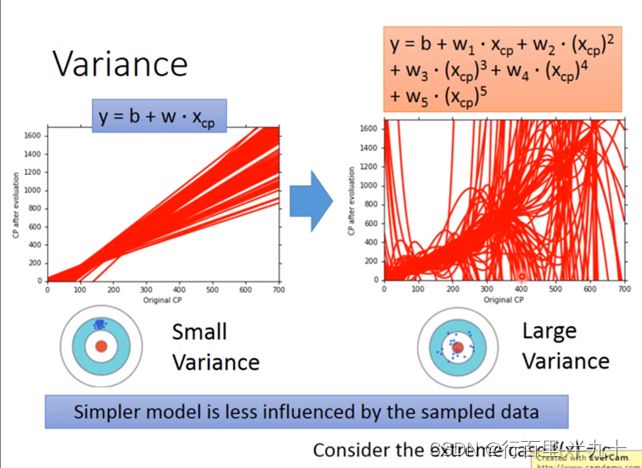
![]() 的variance取决于model的复杂程度和data的数量
的variance取决于model的复杂程度和data的数量
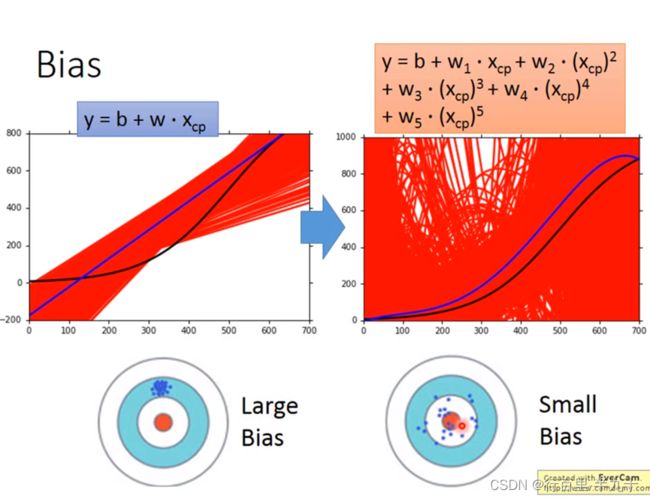
复杂的模型方差相差较大,但是偏差很小;简单模型:偏差大,方差小。如果实际error主要来自于variance很大,这个状况就是overfitting过拟合;如果实际error主要来自于bias很大,这个状况就是underfitting欠拟合
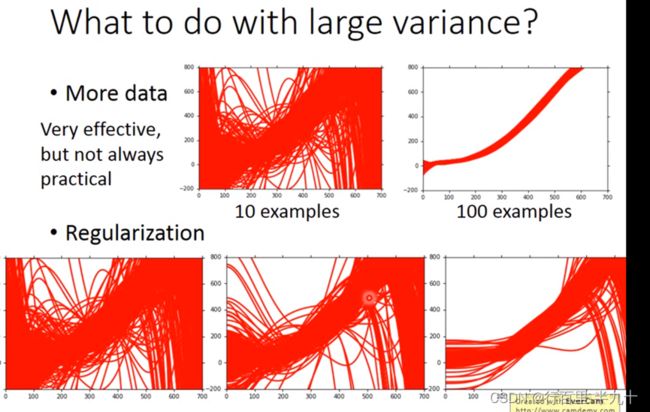
偏差大:模型不能匹配训练样本,欠拟合 → 增加输入特征;更复杂的模型
方差大:训练数据匹配,但测试数据误差大,过拟合 → 更多数据:正则化
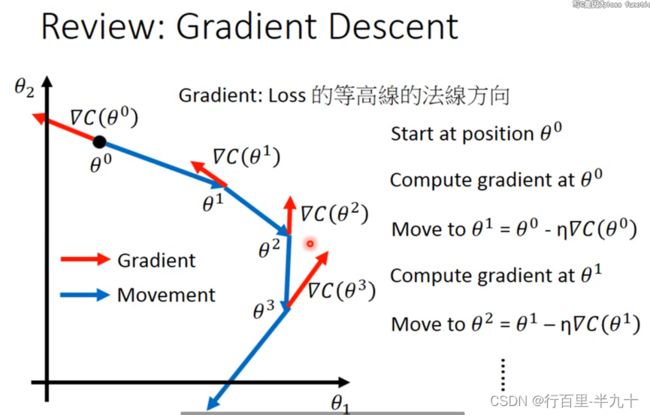
Gradient Descent
红色箭头是指在这点的梯度,蓝色箭头方向代表着梯度下降的方向。
Learning Rate
gradient descent过程中,影响结果的一个关键的因素就是learning rate的大小
如果learning rate刚刚好,就可以像下图中红色线段一样
如果learning rate太小的话,像下图中的蓝色线段,虽然最后能够走到local minimal的地方,但是它可能会走得非常慢。
如果learning rate太大,像下图中的绿色线段,它的步伐太大了,它永远没有办法走到特别低的地方,可能永远在这个“山谷”的口上振荡而无法走下去
如果learning rate非常大,就会像下图中的黄色线段,一瞬间就飞出去了,结果会造成update参数以后,loss反而会越来越大
在设置learning rate 的时候需要谨慎。
Adaptive Learning Rates
最基本、最简单的大原则是:learning rate通常是随着参数的update越来越小的
因为在起始点的时候,通常是离最低点是比较远的,这时候步伐就要跨大一点;而经过几次update以后,会比较靠近目标,这时候就应该减小learning rate,让它能够收敛在最低点的地方
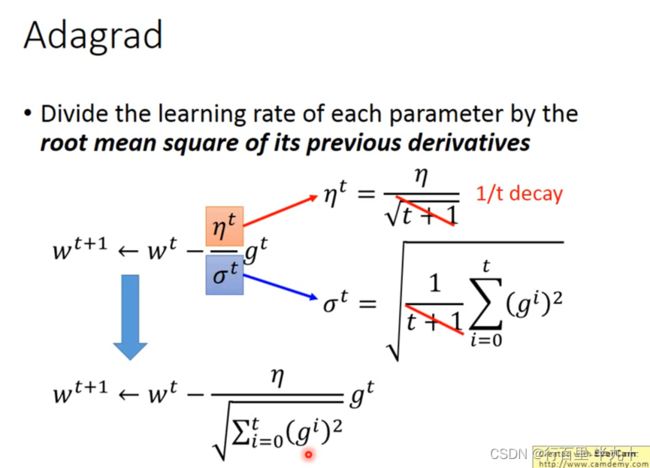
Adagrad(adaptive gradient algorithm)自适应梯度算法
Adagrad就是将不同参数的learning rate分开考虑的一种算法
将每个参数的学习速度除以其先前导数的平方平均数(均方根)
Stochastic Gradient Descent(随机梯度下降)
随机梯度下降的方法可以让训练更快速,传统的gradient descent的思路是看完所有的样本点之后再构建loss function,然后去update参数;而stochastic gradient descent的做法是,看到一个样本点就update一次,因此它的loss function不是所有样本点的error平方和,而是这个随机样本点的error平方
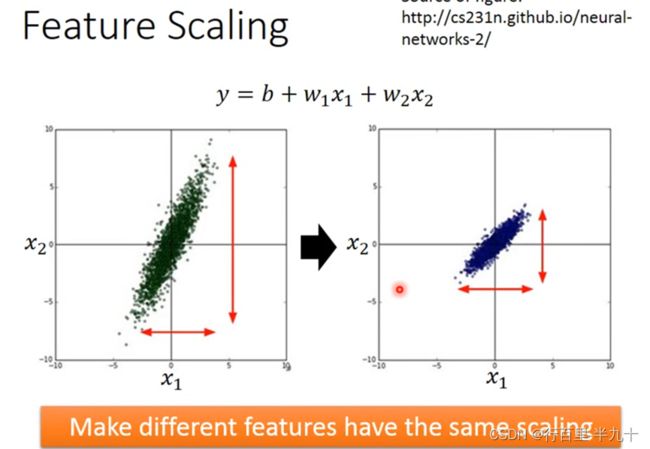
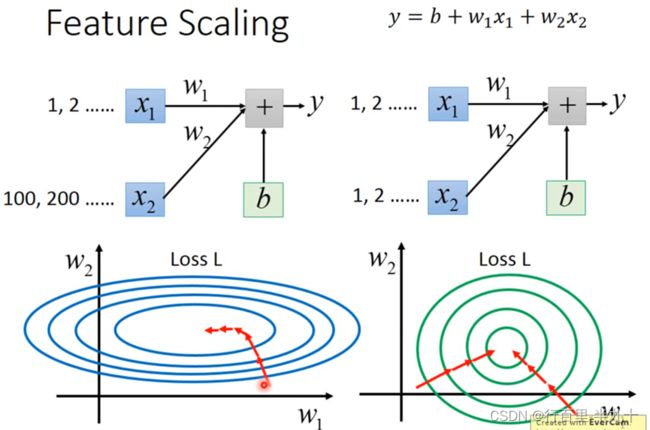
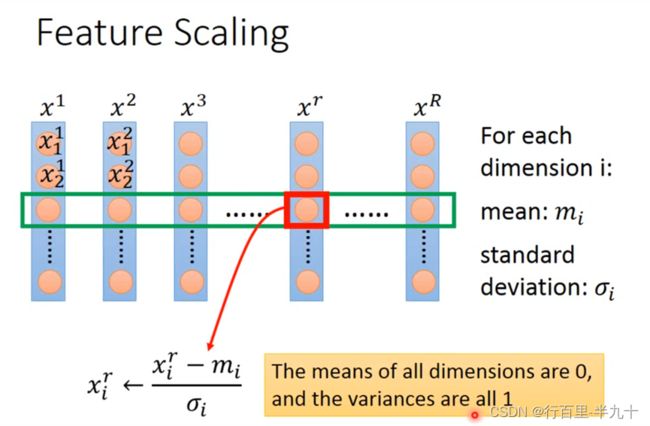
Feature Scaling(特征归一化)
左边的error surface表示,w1对y的影响比较小,所以w1对loss是有比较小的偏微分的,因此在w1的方向上图像是比较平滑的;w2对y的影响比较大,所以w2对loss的影响比较大,因此在w2的方向上图像是比较sharp的
归一化的优点:寻优解的寻优过程会变得平缓,加快了梯度下降求最优解的速度
Gradient Descent的限制
gradient descent的限制是,它在gradient即微分值接近于0的地方就会停下来,而这个地方不一定是global minima,它可能是local minima,可能是saddle point鞍点,甚至可能是一个loss很高的plateau平缓高原
Classification
分类问题是找一个function,它的input是一个object,它的输出是这个object属于哪一个class
Training data for Classification
假设我们把编号400以下的宝可梦当做training data,编号400以上的当做testing data,,如果看到新的宝可梦,能不能够预测它是哪种属性。
Classification as Regression?
以binary classification为例,我们在Training时让输入为class 1的输出为1,输入为class 2的输出为-1;那么在testing的时候,regression的output是一个数值,它接近1则说明它是class 1,它接近-1则说明它是class 2。
这些output远大于1的点,它对于绿线对应的model来说是error,是不好的,所以这组样本点通过Regression训练出来的model,会是紫色这条分界线对应的model。
Regression的output是连续性质的数值,而classification要求的output是离散性质的点,我们很难找到一个Regression的function使大部分样本点的output都集中在某几个离散的点附近。
Ideal Alternatives
loss function定义为即这个model在的training data预测错误的次数,但是这个loss function没有办法微分,是无法用gradient descent的方法去解。
Solution:Generative model
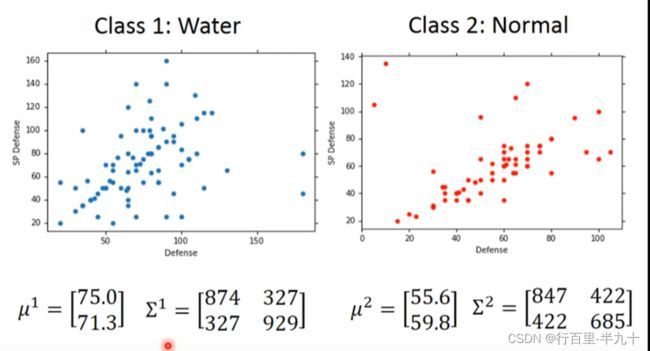
我们想要知道x属于class 1或是class 2的概率,只需要知道4个值, 我们需要从Training data中估测出这四个值
Prior
P(C1)和P(C2)被称为Prior,计算这两个值还是比较简单,主要问题是求P(x∣C1)和P(x∣C2)。
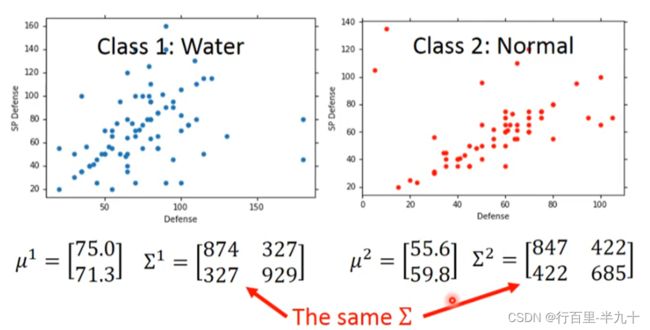
假设我们的x是一只海龟,是水系的,但是在我们79只水系的宝可梦training data里面没有海龟,所以挑一只海龟出来的可能性根本就是0
假设海龟的vector是[103 45],虽然这个点在已有的数据里并没有出现过,但是不可以认为它出现的概率为0,需要用已有的数据去估测海龟出现的可能性
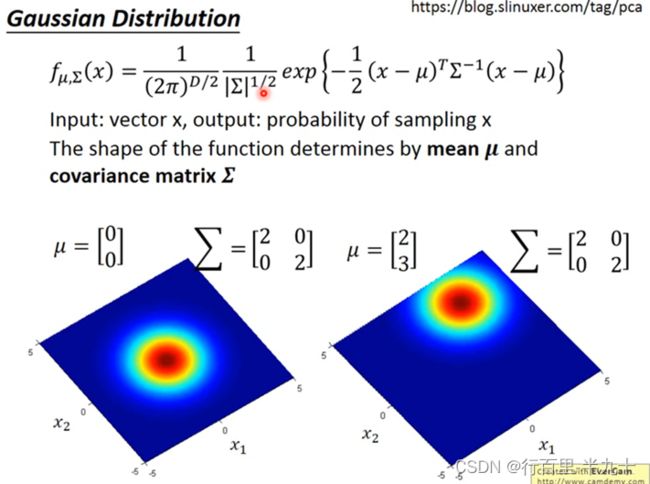
Gaussian Distribution
从图中可以看出,同样的Σ,不同的µ正在上传…重新上传取消,概率分布最高点的地方是不一样的
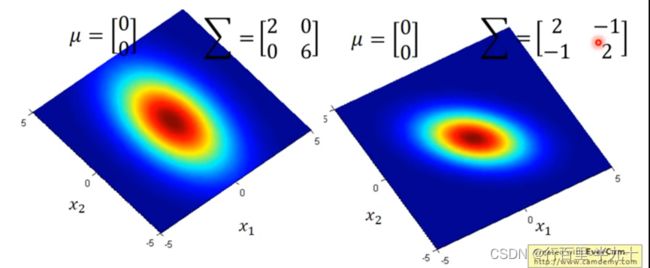
同样的µ,不同的Σ,概率分布最高点的地方是一样的,但是分布的密集程度是不一样的.
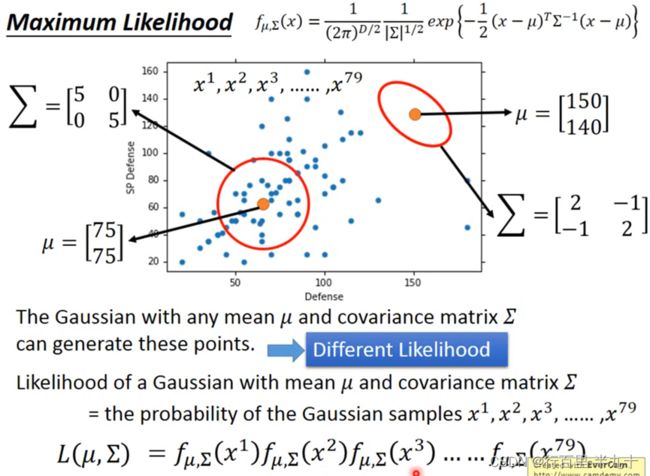
那接下来的问题就是怎么去找出这个Gaussian,只需要去估测出这个Gaussian的均值和协方差即可
Maximum Likelihood
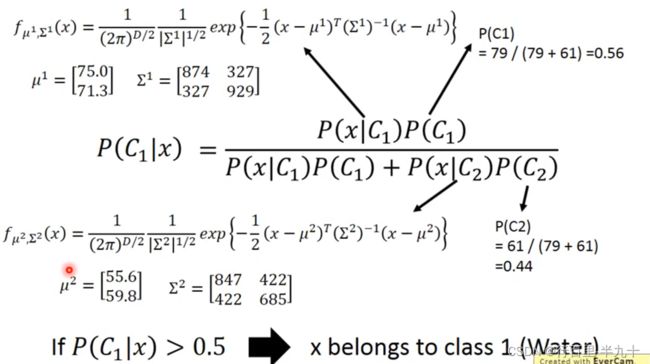
Do Classification
Modifying Model
不同的class可以共用同一个cocovariance matrix
均值不变,而Σ则是原先两个Σ的加权
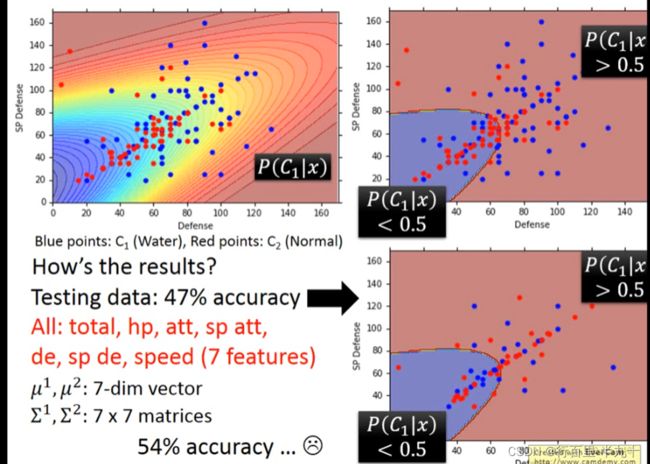
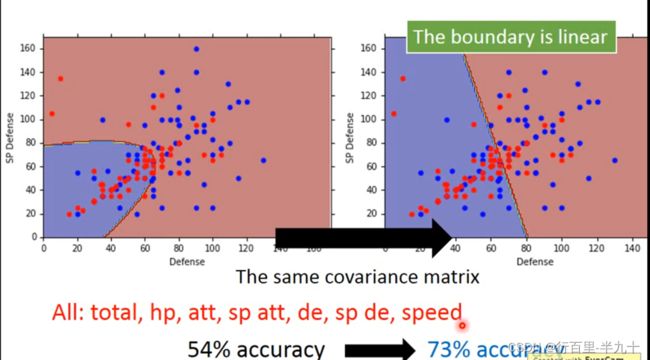
class 1和class 2在没有共用covariance matrix之前,它们的分界线是一条曲线;共用covariance matrix的话,它们之间的分界线就会变成一条直线。正确率由原来的54%的正确率就会变成73%。
Three Steps of classification
Probability distribution
总之,寻找model总的原则是,尽量减少不必要的参数,但是必然的参数绝对不能少