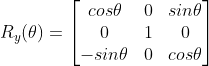机器人欧拉角转化为旋转矩阵

定义：欧拉角和旋转矩阵表示刚体在三维空间中的旋转，欧拉角（O，A，T）

形式：欧拉角形式可分为十二种，有XYZ,XZY,YZX,YXZ,ZXY,ZYX,XYX,XZX,YXY,YZY,ZXZ,ZYZ;其转换形式要根据机器人设定生成形式决定

公式：

如果旋转角度是绕X轴

     

如果旋转角度是绕Y轴

如果旋转角度是绕Z轴

下面以XYZ形式为例，R=Rz*RY*Rx,根据旋转轴确定旋转矩阵，最终的旋转矩阵是从结尾往前相乘。 

代码（部分）

//机器人姿态欧拉角转化为旋转矩阵
void calibration::elur_translate_Rotation(Mat theta, Mat &R, string seq) {
	
	theta /= (180 / CV_PI);

	Mat R_X = (Mat_(3, 3) <<
		1, 0, 0,
		0, cos(theta.at(0, 0)), -sin(theta.at(0, 0)),
		0, sin(theta.at(0, 0)), cos(theta.at(0, 0)));
	Mat R_Y = (Mat_(3, 3) <<
		cos(theta.at(0, 1)), 0, sin(theta.at(0, 1)),
		0, 1, 0,
		-sin(theta.at(0, 1)), 0, cos(theta.at(0, 1)));
	Mat R_X2 = (Mat_(3, 3) <<
		1,0,0,
		0,cos(theta.at(0, 1)), -sin(theta.at(0, 1)),
		0,sin(theta.at(0, 1)), cos(theta.at(0, 1)));
	Mat R_Z = (Mat_(3, 3) <<
		cos(theta.at(0, 2)), -sin(theta.at(0, 2)), 0,
		sin(theta.at(0, 2)), cos(theta.at(0, 2)), 0,
		0, 0, 1);
	Mat R_Z1= (Mat_(3, 3) <<
		cos(theta.at(0, 0)), -sin(theta.at(0, 0)),0,
		sin(theta.at(0, 0)), cos(theta.at(0, 0)),0,
		0,0,1);
	if (seq == "zyx") R = R_X * R_Y * R_Z;
	else if (seq == "yzx") R = R_X * R_Z * R_Y;
	else if (seq == "zxy") R = R_Y * R_X * R_Z;
	else if (seq == "yxz") R = R_Z * R_X * R_Y;
	else if (seq == "xyz") R = R_Z * R_Y * R_X;
	else if (seq == "xzy") R = R_Y * R_Z * R_X;
	else if (seq == "zyz") R = R_Z1 * R_Y*R_Z;
	else if (seq == "zxz") R = R_Z * R_X2*R_Z1;
	else
	{
		cout << "Euler Angle Sequence string is wrong...";
	}
}