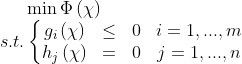Local optimal and global optimal both are optimal

        在学习最优控制过程中，我们经常会遇到局部最优解和全局最优解这两个概念。理解这两个概念对我们学习最优控制的基础：复杂的最优控制问题一般存在许多局部最优解，从这些局部最优解中求解全局最优解往往是费时且意义不大的；因此我们经常使用局部最有解来代替全局最优，进行控制量的设定。

        复杂的最优控制问题往往具有多维控制变量，我们很难掌握其全部信息，因此对于理解其局部最优解和全局最优解存在障碍。在这里，我使用两个简单的例子来使得我们对于这两个概念具有直观上的认识。

        一般最优控制问题被表示为具有如下形式的NLP问题：

         我们首先考虑符合上式形式的如下问题：

这一问题我们很容得知为最优解。画出图像亦可得到上述结论：

我使用CasADi求解上述问题，给定初始解为（绿点），最终求得最优解为（红点）。不难发现在这一问题中仅存在一个局部最优解，所以该局部最优解亦是全局最优解。

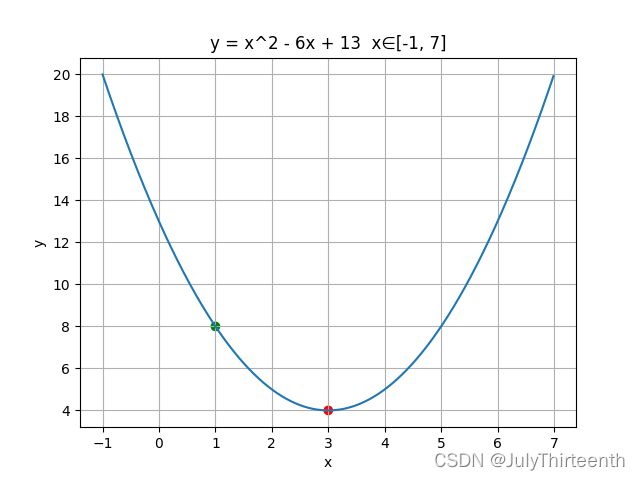
        上述函数在最优控制问题里并不常见。在这里，我们再考虑如下问题：

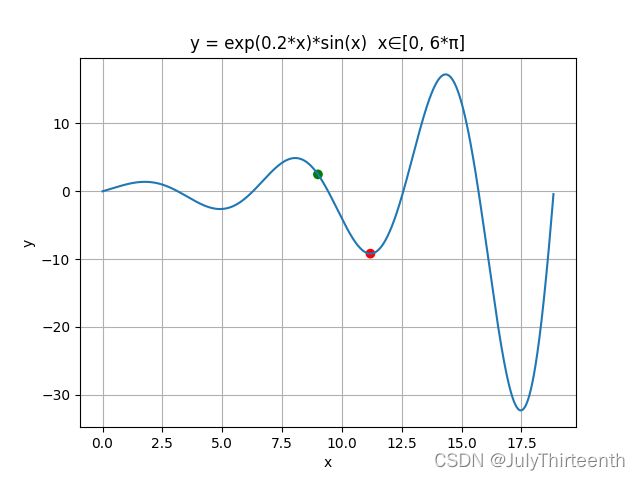
上述问题的函数图像如下图所示：

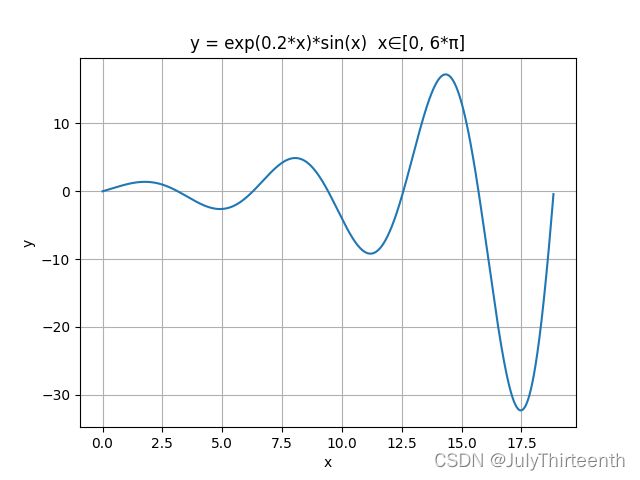
不难发现在该问题中存在多个局部最优解。我使用CasADi求解上述问题，给定初始解为（绿点），最终求得最优解为（红点）。 如下图所示：

此时，由于函数具有多个局部最优解，我们求得的局部最优解显然不是全局最优解。

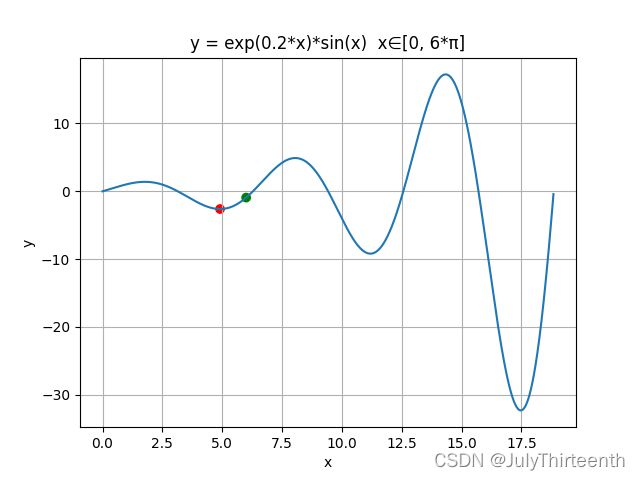
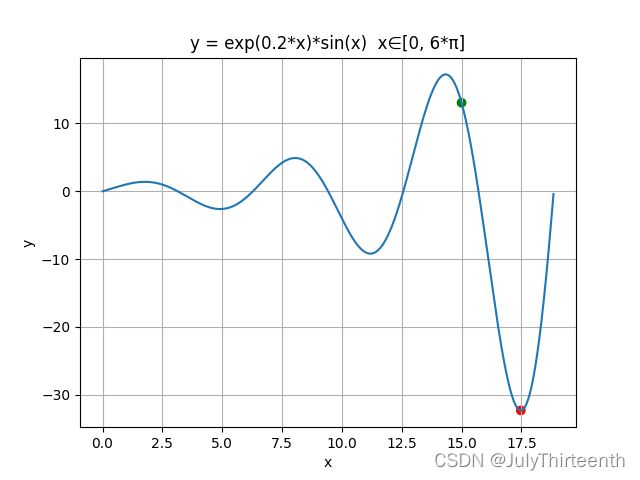
        在这里，我们需要注意：NLP问题的求解对初始解是敏感的。不同的初始解求解得到的局部最优解往往不同，高质量的初始解往往使我们求解NLP问题更加迅速且所得解的质量较高。如下面两幅图所示（初始解分别为）：

        通过以上介绍，我们可以得到对最优控制问题中的局部最优解和全局最优解的直观认识。不难发现，局部最优和全局最优都是最优解，只是在不同初始解的情况下求得的最优解不同。所以在求解最优控制问题时得到一个高质量初始解往往很关键！

 Appendix：

上述问题求解与可视化代码

import casadi as ca
import matplotlib.pyplot as plt
import numpy as np


def plot(init=None, sol=None):
    # Data for plotting
    x = np.arange(0.0, 6 * np.pi, 0.01)
    y = np.exp(0.2 * x) * np.sin(x)
    fig, ax = plt.subplots()
    ax.plot(x, y)
    ax.set(xlabel='x', ylabel='y',
           title='y = exp(0.2*x)*sin(x)  x∈[0, 6*π]')
    ax.grid()

    if init is None or sol is None:
        fig.savefig("1.png")
        plt.show()
    else:
        plt.scatter([init[0], sol[0]], [init[1], sol[1]], c=["green", "red"])
        fig.savefig("2.png")
        plt.show()


def main():
    plot()
    var = ca.SX.sym('x')
    obj = ca.exp(0.2 * var) * ca.sin(var)
    # obj = var ** 2 - 6 * var + 13
    g = []
    p = []
    nlp_prob = {'x': var, 'f': obj, 'g': g, 'p': p}
    opt_sett = {'ipopt.max_iter': 1000, 'ipopt.print_level': 3, 'print_time': 0, 'ipopt.acceptable_tol': 1e-8,
                'ipopt.acceptable_obj_change_tol': 1e-6}
    solver = ca.nlpsol('solver', 'ipopt', nlp_prob, opt_sett)
    init_sol = 15
    param = []
    lbx = 0
    ubx = 6 * ca.pi
    lbg = -ca.inf
    ubg = ca.inf
    sol = solver(x0=init_sol, p=param, lbx=lbx, ubx=ubx, lbg=lbg, ubg=ubg)
    x_sol = sol['x']
    f_sol = sol['f']
    print('x_sol: {}; f_sol: {}.'.format(x_sol, f_sol))
    plot([init_sol, np.exp(0.2 * init_sol) * np.sin(init_sol)], [x_sol, f_sol])


if __name__ == '__main__':
    main()