深度学习 | 一文掌握CNN卷积神经网络（4.3）

最近在恶补深度学习基础知识，以下为根据公众号“ 阿力阿哩哩”的《一文掌握CNN卷积神经网络》而总结的内容。可以结合作者在哔哩大学的视频。

本篇主要写cnn卷积神经网络，我写过一个博客，详细介绍了卷积，可以去看这篇更详细：
OpenCV笔记021————Image Convolution（卷积看这里）

4.3 CNN卷积神经网络

我们在4.2节讲到了神经网络已经逐步成为人类智能生活的璀璨明珠，并介绍了全连接神经网络的整个训练过程（深度学习开端-全连接神经网络），整个流程紧凑而又科学，似乎全连接神经网络已经能解决很多问题了，但细心的读者会发现笔者并没有提及全连接神经网络的缺点。因此，这一节笔者正好通过全连接神经网络的缺点来开展CNN卷积神经网络（Convolutional Neural Network）的教学。

4.3.1 全连接神经网络的缺点

为了讲清全连接神经网络的局限性，笔者还是拿出上一节最简单的全连接网络结构图来讲解，如图4.3所示，相信大家对这个图也不陌生了。设想一下，我们为了求解损失Loss 列出了关于w，b 的方程，并通过梯度下降的方法去求解最佳的（w , b），从而得到最小的损失Loss。换言之，4.2节的内容简单来讲就是站在山上找最陡峭的地方（梯度），不断地往下走，一直走到山谷，这时候我们所在坐标（w , b）就是Loss方程的最优解。

为此，针对图 4.3的这个网络结构，我们要对隐藏层和输出层求4个偏导，又因为隐藏层的输出作为输出层的输入，这时我们就要用到求偏导的链式法则，公式如下：

由公式（4.14）~（4.19），我们可以看出，两个神经元，为了求出隐藏层和输出层最佳的（w , b），我们就要求四个偏导，期间还得为链式求导付出3次连乘的代价。

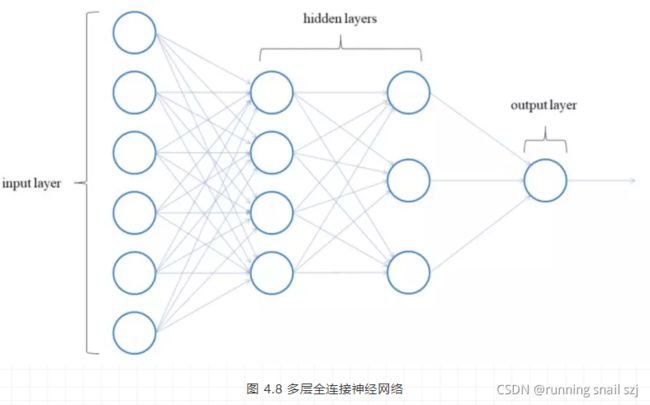
现在，重点来了，如图 4.8所示，倘若我们的网络层次越深，偏导连乘也就越多，付出的计算代价也就越大。

紧接着，一个网络层不单止一个神经元，它可能会有多个神经元，那么多个神经元的输出作为下一级神经元的输入时，就会形成多个复杂的嵌套关系。

我们知道全连接神经网络层级之间都是全连接的，所以网络结构越复杂，那要求的（w , b）就会非常多，整个网络就会收敛得非常慢，这是我们所不希望看到的。这就是全连接神经网络的局限性，特别是针对图像这些冗余信息特别多的输入，如果用全连接神经网络去训练，简直就是一场计算灾难。那么既然问题出现了，就会有人提出解决方法。这时候CNN卷积神经网络便应运而生了。

4.3.2 CNN卷积神经网络原理

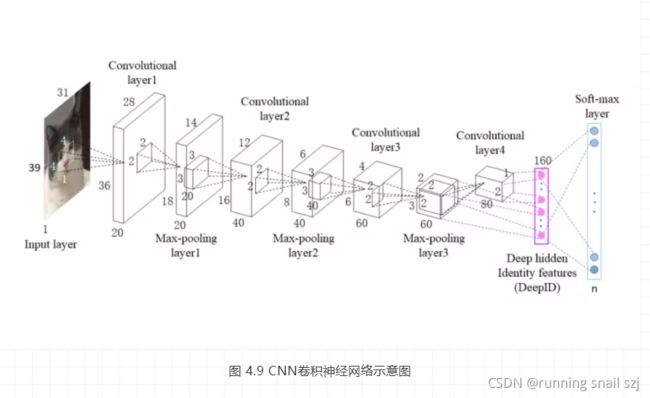
说了这么多，笔者这就给大家附上一张CNN网络结构图，如图 4.9所示，让大家都有个直观的了解。大家可以看到一个经典的CNN网络结构一般包含输入层（Input layer）、卷积层（convolutional layer）、池化层（pooling layer）和输出层（全连接层＋softmax layer）。虽说目前除了输入层，咱啥也不认识，不过，不要慌，接下来就是剖析CNN的精彩时刻。

4.3.3 卷积神经网络与全连接神经网络的区别

• 总有至少1个的卷积层，用以提取特征。
• 卷积层级之间的神经元是局部连接和权值共享，这样的设计大大减少了（w , b）的数量，加快了训练。

以上便是卷积神经网络的特点，为了让大家更清晰地了解这个网络结构的特点，笔者接下来将分别对它的两个特性和特有的网络层次进行详细讲解。

4.3.4 卷积层（Convolutional Layer）

前面我们提到，图像拥有很多冗余的信息，而且往往作为输入信息，它的矩阵又非常大，利用全连接神经网络去训练的话，计算量非常大，前人为此提出了CNN，它的亮点之一就是拥有卷积层。

大家可以想象一下，如果信息过于冗余，那么我们能否去除冗余取出精华部分呢？对，卷积层就是干这个的，通俗易懂来说就是压缩提纯。

那卷积层又是如何工作的呢？大家可以看下图 4.9的CNN网络结构图。卷积层里面有个小框框，那个就是卷积核（Convolutional Kernel），压缩提纯的工作主要通过它来实现的。

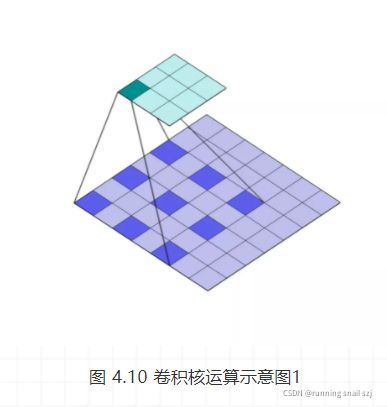
现在，笔者再附上一张图，如图 4.10，让大家明白卷积核是怎么工作的，我们可以把蓝色矩阵看做卷积层的上一层，绿色矩阵看做卷积层，在蓝色矩阵上蠕动的便是卷积核，卷积核通过与他所覆盖蓝色矩阵的一部分进行卷积运算，然后把结果映射到绿色矩阵中。

那么接下来我们要了解卷积核是如何将结果映射到卷积层的。如图 4.11所示。

现在大家也看到了，卷积核在滑动过程中做的卷积运算就是卷积核w 与其所覆盖的区域的数进行点积，最后将结果映射到卷积层。具体的运算公式如式（4.20）所示。

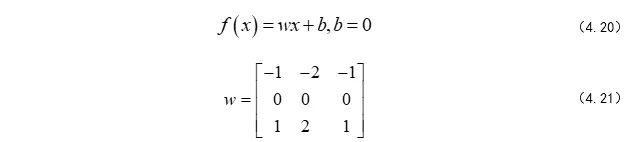
这样看来，我们将9个点的信息量，压缩成了1个点，也就是有损压缩，这个过程我们也可以认为是特征提取。

公式中(w , b）和之前全连接神经网络并没有区别，就是权值w 和偏置b ，它们在初始化之后，随着整个训练过程一轮又一轮的迭代逐渐趋向于最优。

在卷积核 之后一般会加一个Relu的激励函数，就跟4.2节介绍的全连接神经网络的神经元计算组合公式（4.1）和（4.2）一样，只不过这里换成了Relu激励函数，而全连接神经网络用的是sigmod激励函数。这么做的目的都是让训练结果更优。

好了，讲到这，大家应该大致明白了卷积层的工作方式，就是个压缩提纯的过程，而且每个卷积层不单止一个卷积核，它是可以多个的，大家又可以看一下图 4.9的CNN网络的卷积层，大家会看到输出的特征图在“变胖”，因为特征图的上一级经过多个卷积核压缩提纯，每个卷积核对应一层，多层叠加当然会“变胖”。

4.3.5 局部连接和权值共享
笔者在全连接神经网络的局限性中提它的网络层与层之间是全连接的，这就导致了整个训练过程要更新多对（w , b），为此CNN特定引入了局部连接和权值共享的两个特性，来减少训练的计算量。

笔者先给大家介绍一下这么做的科学性在哪？图像或者语言亦或者文本都是冗余信息特别多的东西，倘若我们依照全连接神经网络那般全连接，也就是将所有信息的权值都考虑进了训练过程。

讲到这，大家应该明白这么设计的用途了吧，没错，就是适当得放弃一些连接（局部连接），不仅可以避免网络将冗余信息都学习进来，同时也和权值共享特性一样减少训练的参数，加快整个网络的收敛。

局部连接与权值共享如图 4.12和图 4.13所示。

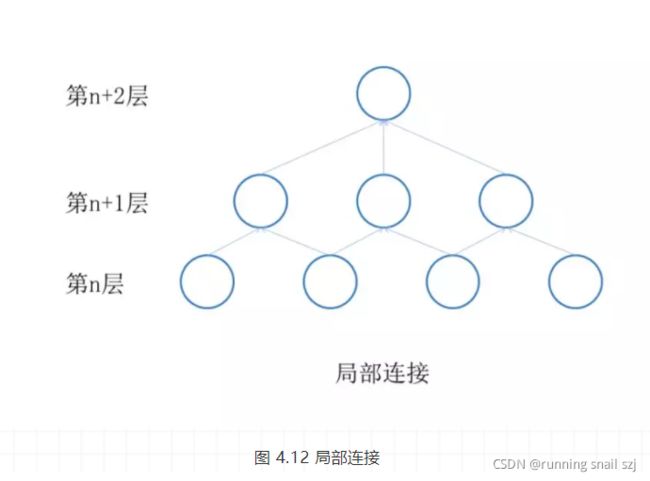
大家可以重点看权值共享这张图，它同时也采用了局部连接，总共就有3*4=12个权值，再加上权值共享，我们就只用求3个权值了，大大减少了我们的计算量。

4.3.6 池化层（Pooling Layer）

一般来说，卷积层后面都会加一个池化层，这时候大家又可以往上看看图 4.9的CNN网络结构了，并且可以将它理解为对卷积层进一步特征抽样，池化层主要分为两种，这时候笔者认为前面说了这么多，现在给大家上一张图，大家应该就明白池化层是何用处。池化层运算如图 4.14所示。

4.3.7 训练

好了，讲到这，我们终于把整个CNN架构特有的层次结构和属性都过了一遍，这时候大家应该大致明白整个CNN架构就是一个不断压缩提纯的过程，目的不单止是为了加快训练速度，同时也是为了放弃冗余信息，避免将没必要的特征都学习进来，保证训练模型的泛化性。

CNN整个训练过程和全连接神经网络差不多，甚至是笔者之后介绍的RNN、LSTM模型，他们的训练过程也和全连接神经网络差不多，唯一不同的就是损失Loss 函数的定义，之后就是不断训练，找出最优的（w , b），完成建模，所以大家搞懂了全连接神经网络的训练过程，就基本吃遍了整个深度学习最重要的数学核心知识了。

这时候，细心的读者们会发现CNN网络结构的输出层也就是softmax层没介绍，是的，笔者现在就开始介绍。CNN损失函数之所以不同也是因为它，这层是CNN的分类层，如图 4.15所示。

softmax层的每一个节点的激励函数

上面的公式，我们可以理解为每个节点输出一个概率，所有节点的概率加和等于1，这也是CNN选择softmax层进行分类的原因所在，可以将一张待分类的图片放进模型，softmax输出的概率中，最大概率所对应的标签便是这张待分类图的标签。

这时候，笔者给大家举个例子就明白了。现在我们的softmax层有3个神经元，也就是说我们可以训练一个分三类的分类器，现在假设我们有一组带标签的训练样本，他们的标签可以如此标记，对应节点标记1，其他标记0。其实就是onehot编码，如图 4.16所示。

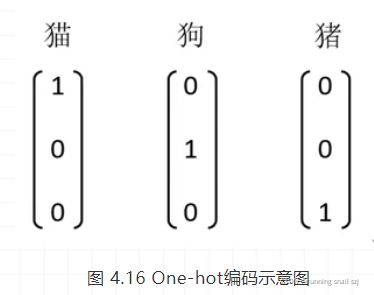
训练的时候将训练样本图片放入输入层，标签向量放入输出层，最终训练出一个模型。

此时，笔者将一张待分类的图片放入我们的模型中，如果最后softmax层输出的结果是结果（4.25）。

这时，大家就明白了上诉公式的含义了，0.85对应着最大概率，说明这张图片是猫。接着所有概率加起来等于1，这样是不是好理解很多啦。好了，讲了这么久，我们还是没有把softmax的损失函数给写出来，它有点特殊，叫交叉熵，如式（4.26）~（4.27）所示。

虽说它长得奇奇怪怪的，但是整体的训练过程和全连接神经网络的思路是一样，都是通过梯度下降法找出最优的（w , b），使Loss 最小，最终完成建模。

4.3.8 CNN卷积神经网络的超参数设置

接下来介绍的内容就比较愉快了，主要是介绍训练CNN网络之前有些参数需要大家手动去设置，行话称之为超参数设置(hyperparameters setting)。

1. 卷积核初始化

卷积核的权值w和偏置b一开始是需要我们人工去初始化的，这里初始化的方法有很多，Tensorflow或者Keras在我们构建卷积层的时候自行给我们初始化了，但是哪天大家心血来潮想自己初始化也是可以的，我们的权值初始化可以根据高斯分布去设置，这样得到的初始化权值更加符合自然规律，毕竟咱们的计算机也是自然界的一部分。

2. Padding

Padding是指对输入图像用多少个像素去填充，如图 4.17所示。

这么做的目的也非常的简单，就是为了保持边界信息，倘若不填充，边界信息被卷积核扫描的次数远比不是中间信息的扫描次数，这样就降低了边界信息的参考价值了。

其次还有另外一个目的是，有可能输入图片的尺寸参差不齐，通过Padding来使所有的输入图像尺寸一致，避免训练过程中没必要的错误。

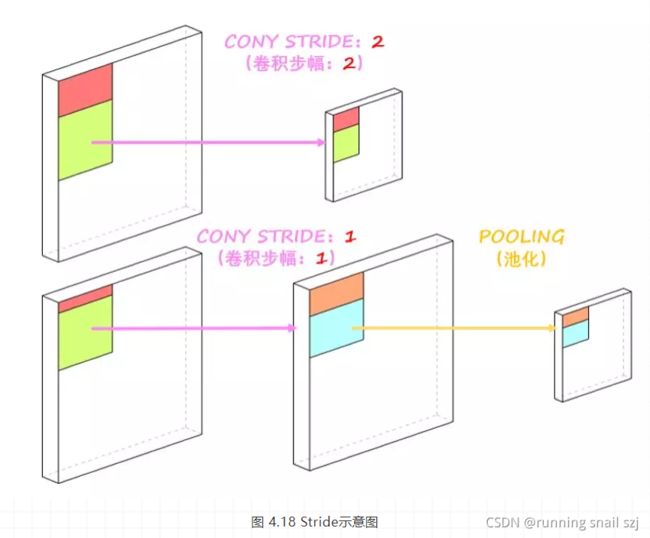
3. Stride步幅

就是卷积核工作的时候，每次滑动的格子数，默认是1，但是也可以自行设置，步幅越大，扫描次数越少，得到的特征也就越“粗糙”，至于如何设置，业界并没有很好的判断方法，也就是说，一切全靠大家自己去试，怎么优秀怎么来。如图 4.18所示。

4.3.9 CNN卷积神经网络小结

上面讲了这么多，其实放在TensorFlow或者Keras里面就是几行代码的事，但是笔者还是倾向于让大家理解整个CNN到底是怎么训练的，它的优点又在哪，这样大家也不至于只知道CNN能用来干嘛，也知道了CNN为什么能这么做，这样对大家以后自己组建一个厉害的网络是很有指导意义的。