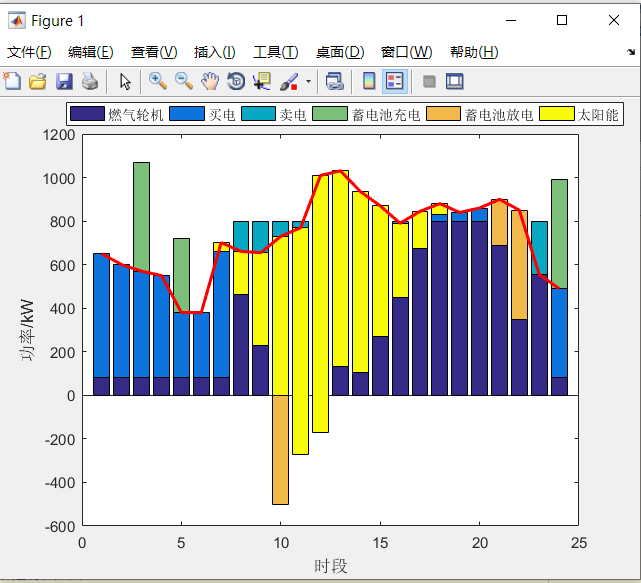
微电网两阶段鲁棒优化经济调度方法(完美复现)
针对微电网内可再生能源和负荷的不确定性,建立了 min-max-min 结构的两阶段鲁棒优化模型,可得到最恶劣场 景下运行成本最低的调度方案。模型中考虑了储能、需求侧 负荷及可控分布式电源等的运行约束和协调控制,并引入了 不确定性调节参数,可灵活调整调度方案的保守性。基于列 约束生成算法和强对偶理论,可将原问题分解为具有混合整 数线性特征的主问题和子问题进行交替求解,从而得到原问 题的最优解。最终通过仿真分析验证了所建模型和求解算法 的有效性,同时给出了分时电价机制下微电网对储能进行调 度的边界条件,可为微电网投资商规划储能及配电网运营商 设计激励机制提供参考。
2、部分代码
function [BBB,UB] = SP(X)
%% 1.参数设置
%燃气轮机参数设置
pg_max=800; %燃气轮机最大功率限制
pg_min=80; %燃气轮机最小功率限制
a=0.67; %燃气轮机成本系数a,b设置
b=0;
%蓄电池参数设置
ps_max=500; %储能允许最大充放电给功率
Es_max=1800; %蓄电池调度过程中允许的最大剩余容量
Es_min=400; %蓄电池调度过程中允许的最小剩余容量
Es_0=1000; %调度过程中初始容量
Ks=0.38; %折算后充放电成本
yita=0.95; %充放电效率
%需求响应负荷参数设置
K_DR=0.32; %需求响应负荷单位调度成本
D_DR=2940; %需求响应总用电需求
D_DR_min=50;
D_DR_max=250;
%配电网交互功率参数设置
pm_max=1500; %微电网与配电网交互功率最大值
%配电网日前交易电价,为24*1向量
price = [0.48;0.48;0.48;0.48;0.48;0.48;0.48;0.9;1.35;1.35;1.35;0.9;0.9;0.9;0.9;0.9;0.9;0.9;1.35;1.35;1.35;1.35;1.35;0.48];
%光伏日前预测,为24*1向量
p_pv_forecast_0 = [0; 0; 0; 0; 0; 0; 40; 200; 500; 860; 1040; 1180; 900; 830; 600; 400; 200; 50; 0; 0; 0; 0; 0; 0];
%p_pv_forecast=[0; 0; 0; 0; 0; 0; 40; 200; 425; 731; 884; 1180; 900; 830; 600; 510; 340; 50; 0; 0; 0; 0; 0; 0]; %初始最坏数据
%负荷日前预测,为24*1向量
p_l_forecast_0=[400; 350; 320; 300; 300; 310; 410; 510; 550; 680; 720; 810; 810; 760; 700; 660; 705; 730; 790; 810; 850; 800; 505; 410];
%p_l_forecast=[400; 350; 320; 300; 300; 310; 451; 561; 605; 748; 720; 810; 891; 836; 770; 726; 775.5; 730; 790; 810; 850; 800; 505; 410]; %初始最坏数据
%
C=[];
c=[a*ones(1,24) Ks*yita*ones(1,24) (Ks/yita)*ones(1,24) zeros(1,24) K_DR*ones(1,48) price' -price' zeros(1,48)];
%% 2.变量设置
%对偶变量设置
miu=sdpvar(192,1); %(h-Fx)'为1*192矩阵,miu必须为192行;子问题约束中G'为240*192矩阵,右侧c为240*1向量,因此miu必须为1列。所以miu为192*1
pai=sdpvar(48,1); %u'为1*48矩阵,pai必须为48行;子问题约束中I'为240*48矩阵,右侧c为240*1向量,因此pai必须为1列。所以pai为192*1
%二元变量B设置
B=binvar(48,1); %B为子问题初始二元变量,取到1即为最坏情况
%% 3.1 设子问题第一行约束
%其中,D为192*240矩阵,d为192*1矩阵
D=[eye(24) zeros(24,216);
-eye(24) zeros(24,216);
zeros(24,24) yita.*tril(ones(24,24),0) -1/yita.*tril(ones(24,24),0) zeros(24,168);
zeros(24,24) -yita.*tril(ones(24,24),0) 1/yita.*tril(ones(24,24),0) zeros(24,168);
zeros(24,72) eye(24) zeros(24,144);
zeros(24,72) -eye(24) zeros(24,144);
zeros(24,96) eye(24) zeros(24,120);
zeros(24,120) eye(24) zeros(24,96);];
d=[pg_min.*ones(24,1);
-pg_max.*ones(24,1);
(Es_min-Es_0).*ones(24,1);
-(Es_max-Es_0).*ones(24,1);
D_DR_min.*ones(24,1);
-D_DR_max.*ones(24,1);
zeros(48,1)];
%其中,K为50*240矩阵,s为50*1矩阵
K=[zeros(1,24) yita.*ones(1,24) -1/yita.*ones(1,24) zeros(1,168);
zeros(1,72) ones(1,24) zeros(1,144);
zeros(24,72) eye(24) eye(24) -eye(24) zeros(24,96);
eye(24) -eye(24) eye(24) -eye(24) zeros(24,48) eye(24) -eye(24) eye(24) -eye(24)];
s=[0;
2940; %总的需求响应
80;70;60;50;70;70;90;100;120;150;160;200;140;100;100;130;140;150;190;200;200;190;100;80; %每个调度时刻的期望需求响应
zeros(24,1)];
%其中,G为192*240矩阵,h为192*1向量,F为192*48矩阵
G=[zeros(24,48) eye(24) zeros(24,168);
zeros(24,48) -eye(24) zeros(24,168);
zeros(24) eye(24) zeros(24,192);
zeros(24) -eye(24) zeros(24,192);
zeros(24,144) eye(24) zeros(24,72);
zeros(24,144) -eye(24) zeros(24,72);
zeros(24,168) eye(24) zeros(24,48);
zeros(24,168) -eye(24) zeros(24,48)];
h=[zeros(72,1);
-ps_max.*ones(24,1);
zeros(72,1);
-pm_max.*ones(24,1)];
F=[zeros(24,48);
ps_max.*eye(24) zeros(24,24);
zeros(24,48);
-ps_max.*eye(24) zeros(24,24);
zeros(24,48);
zeros(24,24) pm_max*eye(24);
zeros(24,48);
zeros(24,24) -pm_max*eye(24);];
%I为48*240矩阵,u为48*1向量
I=[zeros(24,192) eye(24) zeros(24);
zeros(24,216) eye(24)];
u0=[p_pv_forecast_0;p_l_forecast_0];
C = [C, D'*gamma+K'*lamda+G'*miu+I'*pai<=c']; %子问题第一行约束
%% 3.2 设立子问题第二、三行约束
delta_u=[0; 0; 0; 0; 0; 0; 6; 30; 75; 129; 156; 177; 135; 124.5; 90; 60; 30; 7.5; 0; 0; 0; 0; 0; 0;
40; 35; 32; 30; 30; 31; 41; 51; 55; 68; 72; 81; 81; 76; 70; 66; 70.5; 73; 79; 81; 85; 80; 50.5; 41];
BB=binvar(48,1); %引入的辅助变量B’,记为BB
C = [C, gamma>=0];
C = [C, miu>=0];
%C = [C, lamda>=0];
%C = [C, pai>=0];
C = [C, BB>=0];
C = [C, 0<=BB,BB<=1000000*B];
%C = [C, BB>=pai-10*(ones(48,1)-B)];
C = [C, pai-1000000*(1-B)<=BB,BB<=pai];
C = [C, sum(B(1:24,:))<=6];
C = [C, sum(B(25:48,:))<=12];
%for k=1:48
% C = [C, BB(k,1)>=0]; %子问题第二行约束前半部分
%C = [C, BB(k,1)<= 10000*B(k,1)]; %子问题第二行约束后半部分
%C = [C, BB(k,1)>= pai(k,1) - 10000* ( 1-B(k,1) ) ]; %子问题第三行约束前半部分
%C = [C, BB(k,1)<= pai(k,1)] ; %子问题第三行约束后半部分
%end
%L1=[ones(1,24) zeros(1,24)];
%L2=[zeros(1,24) ones(1,24)];
%C = [C, L1*B<=12];
%C = [C, L2*B<=12];
%% 4.设目标函数
Z= -(d'*gamma+s'*lamda+(h-F*X)'*miu+u0'*B+delta_u'*BB);
%% 5.求解
ops = sdpsettings('solver','cplex');
result = optimize(C,Z,ops);
BBB=value(B);
BBBB=value(BB);
GAMMA=value(gamma);
LAMDA=value(lamda);
MIU=value(miu);
PAI=value(pai);
UB=value(-Z);