基于改进蜂群算法和灰色模型的管道腐蚀预测 - 附代码
基于改进蜂群算法和灰色模型的管道腐蚀预测 - 附代码
文章目录
- 基于改进蜂群算法和灰色模型的管道腐蚀预测 - 附代码
-
- 1.灰色模型(GM( 1,1) )原理
- 2.GM(1,1)模型优化
-
- 2.1 原始数据序列预处理
- 2.2 背景值优化
- 4.管道腐蚀预测
- 3.参考文献
- 4.Matlab代码
摘要:为了解决缺少大量数据样本情况下油气管道剩余寿命预测问题,采用 GM( 1,1) 模型预测管道腐蚀趋势。考虑到 GM( 1,1) 模型自身存在的缺陷,采用指数变换预处理原始数据和动态生成系数重构背景值两种方法改进GM( 1,1) 模型的建模过程,并运用改进的蜂群算法( IABC) 求解全局最优动态生成系数,进而建立改进的蜂群算法优化的指数变换灰色模型( IABC-EGM( 1,1) ) ;
1.灰色模型(GM( 1,1) )原理
灰色预测 GM( 1,1) 模型利用原始序列累加生成新的序列,使原本混乱的数据呈现出规律性,即使
只有较少的数据,也能得到良好的预测结果,其一般包括累加生成、建模求解、累减还原 3 个步骤,具体如下:
1)累加生成。
设 X ( 0 ) = { x ( 0 ) ( 1 ) , x ( 0 ) ( 2 ) , . . . , x ( 0 ) ( n ) } X^{(0)}=\{x^{(0)}(1),x^{(0)}(2),...,x^{(0)}(n)\} X(0)={x(0)(1),x(0)(2),...,x(0)(n)}为原始非负数据序列;则 X ( 1 ) = { x ( 1 ) ( 1 ) , x ( 1 ) ( 2 ) , . . . , x ( 1 ) ( n ) } X^{(1)}=\{x^{(1)}(1),x^{(1)}(2),...,x^{(1)}(n)\} X(1)={x(1)(1),x(1)(2),...,x(1)(n)}为 X ( 0 ) X^{(0)} X(0) 的一阶累加生成序列,其中:
x ( 1 ) ( k ) = ∑ i = 1 k x ( 0 ) ( i ) (1) x^{(1)}(k)=\sum_{i=1}^kx^{(0)}(i)\tag{1} x(1)(k)=i=1∑kx(0)(i)(1)
式子中, k = 1 , 2 , . . . , n k=1,2,...,n k=1,2,...,n
则 Z ( 1 ) = { z ( 1 ) ( 2 ) , z ( 1 ) ( 3 ) , . . . , z ( 1 ) ( n ) } Z^{(1)}=\{z^{(1)}(2),z^{(1)}(3),...,z^{(1)}(n)\} Z(1)={z(1)(2),z(1)(3),...,z(1)(n)}为 X ( 1 ) X^{(1)} X(1)的紧邻均值生成序列,其中:
z ( 1 ) ( k ) = 1 2 [ x ( 1 ) ( k ) + x ( 1 ) ( k − 1 ) ] (2) z^{(1)}(k)=\frac{1}{2}[x^{(1)}(k)+x^{(1)}(k-1)]\tag{2} z(1)(k)=21[x(1)(k)+x(1)(k−1)](2)
式子中, k = 2 , 3 , . . . , n k=2,3,...,n k=2,3,...,n
2)建模求解
x ( 0 ) ( k ) + a z ( 1 ) ( k ) = b x^{(0)}(k)+az^{(1)}(k)=b x(0)(k)+az(1)(k)=b为 GM( 1,1)模型的灰微分方程,其白化微分方程为:
d x ( 1 ) ( t ) d t + a x ( 1 ) ( t ) = b (3) \frac{dx^{(1)}(t)}{dt}+ax^{(1)}(t)=b\tag{3} dtdx(1)(t)+ax(1)(t)=b(3)
式中, a a a 为发展系数, b b b 为灰色作用量,均为待解参数,可通过最小二乘法估计 a a a 和 b b b 的值。
( a , b ) T = ( B T B ) − 1 B T Y (4) (a,b)^T=(B^TB)^{-1}B^TY \tag{4} (a,b)T=(BTB)−1BTY(4)
式中, B = [ − z ( 1 ) ( 2 ) 1 − z ( 1 ) ( 3 ) 1 . . . . . . − z ( 1 ) ( n ) 1 ] B=\left[\begin{matrix} -z^{(1)}(2)&1\\ -z^{(1)}(3)&1\\ ...&...\\ -z^{(1)}(n)&1\\ \end{matrix}\right] B=⎣⎢⎢⎡−z(1)(2)−z(1)(3)...−z(1)(n)11...1⎦⎥⎥⎤, Y = [ x ( 0 ) ( 2 ) x ( 0 ) ( 3 ) . . . x ( 0 ) ( n ) ] Y=\left[\begin{matrix} x^{(0)}(2)\\ x^{(0)}(3)\\ ...\\ x^{(0)}(n)\\ \end{matrix}\right] Y=⎣⎢⎢⎡x(0)(2)x(0)(3)...x(0)(n)⎦⎥⎥⎤
则白化微分方程的解为:
x ( 1 ) ( t ) = b a + [ x ( 1 ) ( 1 ) − b a ] e − a ( t − 1 ) (5) x^{(1)}(t)=\frac{b}{a}+[x^{(1)}(1)-\frac{b}{a}]e^{-a(t-1)}\tag{5} x(1)(t)=ab+[x(1)(1)−ab]e−a(t−1)(5)
GM( 1,1) 模型的时间响应序列为:
x ( 1 ) ( k + 1 ) ∗ = b a + [ x ( 0 ) ( 1 ) − b a ] e − a k (6) x^{(1)}(k+1)^*=\frac{b}{a}+[x^{(0)}(1)-\frac{b}{a}]e^{-ak}\tag{6} x(1)(k+1)∗=ab+[x(0)(1)−ab]e−ak(6)
式子中, k = 1 , 2 , . . . , n − 1 k=1,2,...,n-1 k=1,2,...,n−1。
3)累减还原。原始数据序列还原值为
x ( 0 ) ( k + 1 ) ∗ = x ( 1 ) ( k + 1 ) ∗ − x ( 1 ) ( k ) ∗ (7) x^{(0)}(k+1)^*=x^{(1)}(k+1)^*-x^{(1)}(k)^*\tag{7} x(0)(k+1)∗=x(1)(k+1)∗−x(1)(k)∗(7)
2.GM(1,1)模型优化
2.1 原始数据序列预处理
当处理某些光滑度不足的数据序列时,灰色模型的精度会大大下降,常见方法是采用数据变换预
处理原始数据以提高其光滑度 。本文采用指数函数变换预处理原始数据,建立指数变换灰色模型
EGM( 1,1) ,具体过程如下。
对原始序列作指数变换
y ( 0 ) ( i ) = c x ( 0 ) ( k ) , i = k = 1 , 2 , . . , n (8) y^{(0)}(i)=c^{x^{(0)}(k)},i=k=1,2,..,n \tag{8} y(0)(i)=cx(0)(k),i=k=1,2,..,n(8)
式中, c c c 为底数。按照 GM( 1,1) 模型对新序列进行建模,得到新的响应序列为:
y ( 1 ) ( k + 1 ) ∗ = b a + [ y ( 0 ) ( 1 ) − b a ] e − a k (9) y^{(1)}(k+1)^* = \frac{b}{a}+[y^{(0)}(1)-\frac{b}{a}]e^{-ak}\tag{9} y(1)(k+1)∗=ab+[y(0)(1)−ab]e−ak(9)
新序列的还原值为
y ( 0 ) ( k + 1 ) ∗ = y ( 1 ) ( k + 1 ) ∗ − y ( 1 ) ( k ) ∗ (10) y^{(0)}(k+1)^*=y^{(1)}(k+1)^*-y^{(1)}(k)^*\tag{10} y(0)(k+1)∗=y(1)(k+1)∗−y(1)(k)∗(10)
由 y ( 0 ) ( i ) = c x ( 0 ) ( k ) y^{(0)}(i)=c^{x^{(0)}(k)} y(0)(i)=cx(0)(k)可得原始序列的还原值为:
x ( 0 ) ( k ) ∗ = l n ( y ( 0 ) ( k ) ∗ ) l n ( c ) (11) x^{(0)}(k)^*=\frac{ln(y^{(0)}(k)^*)}{ln(c)}\tag{11} x(0)(k)∗=ln(c)ln(y(0)(k)∗)(11)
2.2 背景值优化
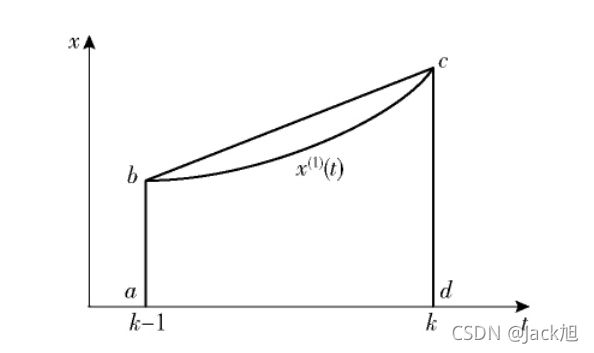
GM( 1,1) 模型的背景值构造公式是存在缺陷的,如图1 所示,真实背景值应该是x ( 1) ( t) 在[k -1,k]区间上的积分,而传统建模方法的背景值是采用梯形面积作为替代。当处理某些剧烈变化的数据时,传统背景值构造方法会带来较大误差,导致模型的精度下降。
基于此,本文采用动态生成系数 α( i) 替代固定值,通过动态调整各区间的生成系数,最大程度降低
背景值误差。新的背景值构造公式为
z ( 1 ) ( k ) = α ( i ) x ( 1 ) ( k ) + ( 1 − α ( i ) ) x ( 1 ) ( k − 1 ) (12) z^{(1)}(k) = \alpha(i)x^{(1)}(k)+(1-\alpha(i))x^{(1)}(k-1) \tag{12} z(1)(k)=α(i)x(1)(k)+(1−α(i))x(1)(k−1)(12)
式中, α ( i ) α(i) α(i) 为动态生成系数, 0 ≤ α ( i ) ≤ 1 , i = 1 , 2 , . . . , n − 1 , k = 2 , 3 , . . . , n 0\leq\alpha(i)\leq1,i=1,2,...,n-1,k=2,3,...,n 0≤α(i)≤1,i=1,2,...,n−1,k=2,3,...,n
由于求解动态生成系数的参数较多,一般的方法难以求解,而蜂群算法在求解非线性、多维的复杂
优化问题时有独特优势,可得到参数的全局最优解,所以采用蜂群算法求解灰色模型的动态生成系数
3.蜂群算法及其改进
具体原理参考参考文献即可
本文的目标函数为加权平方误差和,其公式为:
m i n ∑ k = 2 n ϕ ( k ) ( x ( 0 ) ( k ) ∗ − x ( 0 ) ( k ) ) 2 (13) min\,\sum_{k=2}^n \phi(k)(x^{(0)}(k)^*-x^{(0)}(k))^2 \tag{13} mink=2∑nϕ(k)(x(0)(k)∗−x(0)(k))2(13)
式中, x ( 0 ) ( k ) x^{(0)}(k) x(0)(k)为建模原始数据序列; x ( 0 ) ( k ) ∗ x^{(0)}(k)^* x(0)(k)∗为模型拟合值; ϕ ( k ) \phi(k) ϕ(k)为加权系数,其值为各平方误差与平方误差和的比值。通过加权系数修正各平方误差和,提高大误差的权重,降低小误差的权重,使总的误差分布更加均匀。
4.管道腐蚀预测
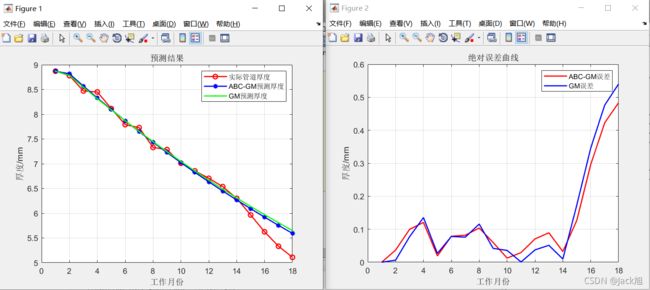
为了检验本文提出的预测模型的有效性,用常压蒸馏塔塔顶换热器入口分配管弯头测厚数据进行比较分析,壁厚测量的平均值见表 1。表中前 12 个工作月的数据作为灰色建模方法的原始序列,后 6 个工作月的数据作为预测序列,用于评估预测方法的准确性。
| 工作月数 | 壁厚/mm |
|---|---|
| 1 | 8.8700 |
| 2 | 8.7800 |
| 3 | 8.4700 |
| 4 | 8.4500 |
| 5 | 8.1150 |
| 6 | 7.7900 |
| 7 | 7.7300 |
| 8 | 7.3300 |
| 9 | 7.2850 |
| 10 | 7.0100 |
| 11 | 6.8550 |
| 12 | 6.7050 |
| 13 | 6.5375 |
| 14 | 6.3000 |
| 15 | 5.9650 |
| 16 | 5.6250 |
| 17 | 5.3325 |
| 18 | 5.1100 |
改进蜂群GM预测数据为:8.87 8.8169 8.5697 8.3294 8.0958 7.8688 7.6482 7.4337 7.2253 7.0227 6.8257 6.6343 6.4483 6.2675 6.0917 5.9209 5.7549 5.5935
**改进蜂群GM的MSE:**0.032463
基础GM预测数据为:8.87 8.7863 8.5472 8.3146 8.0883 7.8682 7.654 7.4457 7.2431 7.046 6.8542 6.6677 6.4862 6.3097 6.1379 5.9709 5.8084 5.6503
基础GM的MSE:0.040304
从结果来看改进算法结果明显优于原始GM算法。
3.参考文献
[1]秦谢勋,刘文彬,陈良超.基于改进蜂群算法和灰色模型的管道腐蚀预测[J].北京化工大学学报(自然科学版),2021,48(01):74-80.