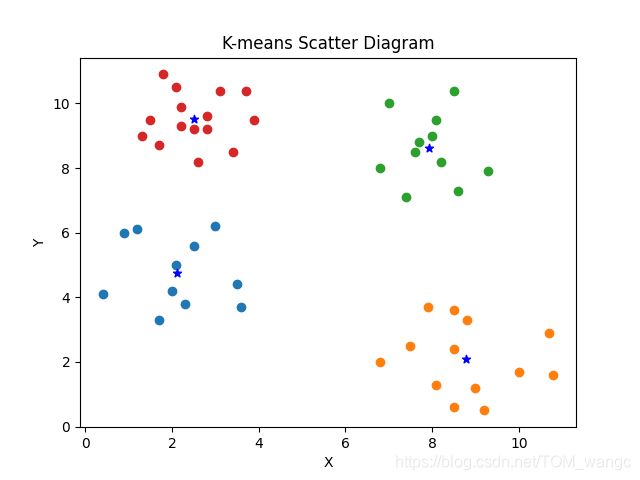
k-means算法实现,--python
k-means算法思想:
第一步,从文件中读取数据,点用元组表示,点集用列表表示。
第二步,初始化聚类中心。首先获取数据的长度,然后在range(0,length)这个区间上随机产生k个不同的值,以此为下标提取出数据点,将它们作为聚类初始中心,产生列表center。
第三步,分配数据点。将数据点分配到距离(欧式距离)最短的聚类中心中,产生列表assigment,并计算平均误差。
第四步,如果首次分配后有结果为空,则重新初始化聚类中心。
第五步,更新聚类中心,(计算每一簇中所有点的平均值),然后再次进行分配,并计算平均误差。
第六步,比较前后两次的平均误差是否相等,若不相等则进行循环,否则终止循环,进入下一步
最少进行两次聚类,对比误差,输出较小误差时的结果,避免平均误差过大。
流程图:
![]()
结论:
import random
from math import *
import matplotlib.pyplot as plt
#从文件种读取数据
def read_data():
data_points = []
with open('data.txt','r') as fp:
for line in fp:
if line =='\n':
continue
data_points.append(tuple(map(float,line.split(' '))))#去掉空格,并将data中数据的类型转为tuple
fp.close()
return data_points
#初始化聚类中心
def begin_cluster_center(data_points,k):
center=[]
length=len(data_points)#长度
rand_data = random.sample(range(0,length), k)#生成k个不同随机数
for i in range(k):#得出k个聚类中心(随机选出)
center.append(data_points[rand_data[i]])
return center
#计算最短距离(欧式距离)
def distance(a,b):
length=len(a)
sum = 0
for i in range(length):
sq = (a[i] - b[i]) ** 2
sum += sq
return sqrt(sum)
#分配样本
# 按照最短距离将所有样本分配到k个聚类中心中的某一个
def assign_points(data_points,center,k):
assignment=[]
for i in range(k):
assignment.append([])
for point in data_points:
min = 10000000
flag = -1
for i in range(k):
value=distance(point,center[i])#计算每个点到聚类中心的距离
if valueend_sum_E:
min_sum_E=end_sum_E
assignment, end_sum_E, end_center, count = k_means(data_points,k)
print_result(count, min_sum_E, k, assignment)#输出结果
plot(k, assignment,end_center)#画图
main() 数据集:
2.0 4.2
2.1 5.0
2.3 3.8
1.2 6.1
3.5 4.4
3.6 3.7
3.0 6.2
2.5 5.6
1.7 3.3
0.9 6.0
0.4 4.1
7.0 10.0
8.0 9.0
8.2 8.2
9.3 7.9
7.4 7.1
6.8 8.0
8.1 9.5
8.5 10.4
7.6 8.5
8.6 7.3
7.7 8.8
1.8 10.9
1.5 9.5
1.7 8.7
1.3 9.0
2.8 9.6
2.2 9.9
2.1 10.5
2.5 9.2
3.1 10.4
3.9 9.5
3.7 10.4
2.6 8.2
2.8 9.2
2.2 9.3
3.4 8.5
8.1 1.3
8.5 2.4
8.8 3.3
9.0 1.2
10.7 2.9
7.9 3.7
7.5 2.5
8.5 0.6
10.8 1.6
9.2 0.5
6.8 2.0
8.5 3.6
10.0 1.7