数字图像处理习题（二）

数字图像处理习题（二）

---

一、编程题

1. 图像的频域处理

1.1 完成清华大学教材例4.3,并做频谱分析

• 编程思路：

  （1）使用fft2()函数，将灰度图像通过快速傅里叶变换算法返回矩阵的二维傅里叶变换。

  （2）使用abs()函数取复数的幅值。对于复数x=a+b*i，有abs(x)=sqrt(a2+b2)。得到原频谱图。

  ​ 为了便于观察，需要把傅里叶规格化到[0 100]。

  （3）使用fftshift()函数将规格化平铺图移位，低频移到频谱图中心。

  （4）使用subplot(),imshow(),title();将原图，原频谱图，移位频谱图同时显示，方便观察实验结果。

• 源代码：

  Homework1_1

  %例4.3
  close all; 
  clear; 
  clc;
  Image = imread('img.jpg');
  grayI = rgb2gray(Image);
  DFTI1 = fft2(grayI);                         %计算离散傅里叶变换
  ADFTI1 = abs(DFTI1);			             %计算傅里叶谱
  top = max(ADFTI1(:));
  bottom = min(ADFTI1(:));
  ADFTI1 = (ADFTI1-bottom)/(top-bottom)*100;   %把傅里叶规格化到[0 100]，便于观察
  ADFTI2 = fftshift(ADFTI1);				     %将规格化频谱图移位，低频移到频谱图中心
  subplot(1,3,1),imshow(Image),title('原图');
  subplot(1,3,2),imshow(ADFTI1),title('原频谱图');
  subplot(1,3,3),imshow(ADFTI2),title('移位频谱图');
  

• 结果：

• 分析：

  （1）图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度。

  （2）FFT是离散傅立叶变换的快速算法，可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了。

  从物理效果看，傅立叶变换是将图像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域。也就意味着傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数，傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数。

  （3）变换之后的图像在原点平移之前四角是低频，最亮（见结果图片原频谱图）。平移之后中间部分是低频，最亮（见结果图片中移位频谱图），亮度大说明低频的能量大（幅角比较大）。

  （4）通过观察傅立叶变换后的频谱图，可以看出图像的能量分布。

  • 如果频谱图中暗的点数更多，那么实际图像是比较柔和的（因为各点与邻域差异都不大，梯度相对较小）。
  • 如果频谱图中亮的点数多，那么实际图像是尖锐的，边界分明且边界两边像素差异较大的。
  • 对频谱移频到原点以后，可以看出图像的频率分布是以原点为圆心，对称分布的。将频谱移频到圆心除了可以清晰地看出图像频率分布以外，还有一个好处，它可以分离出有周期性规律的干扰信号，比如正弦干扰，一副带有正弦干扰，移频到原点的频谱图上可以看出除了中心以外还存在以某一点为中心，对称分布的亮点集合，这个集合就是干扰噪音产生的，这时可以很直观的通过在该位置放置带阻滤波器消除干扰。

1.2 利用傅里叶变换实现频域低通滤波(巴特沃斯、指数、梯形三种)，并进行比较分析。

1.2.1 巴特沃斯

• 编程思路：

  （1）读取原始图像，对图像进行灰度化处理。

  （2）用imnoise(Image,'gaussian')添加高斯噪声

  （3）通过fftshift(fft2(double(Image)))计算傅里叶谱，并傅里叶变换的结果进行平移，得到移位频谱图。

  （4）对图像进行巴特沃斯低通滤波处理。

  • d0表示截止频率。
  • n表示的是巴特沃斯滤波器的阶数，控制曲线的衰减速度。
  • 随着阶数n的增加，振铃效应会越来越明显。指数、梯形低通滤波器同理，根据函数，给定参数。

  （5）用real(ifft2(ifftshift(g)))对滤波后的频谱进行反傅里叶变换，得到滤波后图像。

• 源代码：

  Homework1_2_1.c

  %利用傅里叶变换实现频域巴特沃斯低通滤波
  close all;
  clear;
  clc;
  Image=rgb2gray(imread('img.jpg'));         %读取原图转变为灰度化图像
  Image=imnoise(Image,'gaussian');           %添加高斯噪声
  subplot(1,5,1),imshow(Image),title('原图'); %添加噪声后的原图
  FImage=fftshift(fft2(double(Image)));      %傅里叶变换及平铺搬移
  [N,M]=size(FImage);                        %获得该图像的行列数
  g=zeros(N,M);
  r1=floor(M/2);
  r2=floor(N/2);
  d0=30;
  n=[1 2 3 4];
  for i=1:4                                  %四阶
      for x=1:M                              %逐像素遍历
          for y=1:N
              d=sqrt((x-r1)^2+(y-r2)^2);
              h=1/(1+(d/d0)^(2*n(i)));
              g(y,x)=h*FImage(y,x);
          end
      end
      g=real(ifft2(ifftshift(g)));
      subplot(1,5,i+1),imshow(uint8(g)),title(['Butterworth低通滤波n=',num2str(n(i))]);
  end
  

• 结果：

1.2.2 指数

• 编程思路：

  （1）读取原始图像，对图像进行灰度化处理。

  （2）用imnoise(Image,'gaussian')添加高斯噪声

  （3）通过fftshift(fft2(double(Image)))计算傅里叶谱，并傅里叶变换的结果进行平移，得到移位频谱图。

  （4）对图像进行指数低通滤波处理。

  （5）对滤波后的频谱进行反傅里叶变换，得到滤波后图像。

• 源代码：

  Homework1_2_2.c

  %利用傅里叶变换实现频域指数低通滤波
  close all;
  clear;
  clc;
  Image=rgb2gray(imread('img.jpg'));       %读取原图转变为灰度化图像
  Image=imnoise(Image,'gaussian');         %添加高斯噪声
  subplot(1,3,1),imshow(Image),title('原图');%添加噪声后的原图
  FImage=fftshift(fft2(double(Image)));    %傅里叶变换及平铺搬移
  [N,M]=size(FImage);
  g=zeros(N,M);
  r1=floor(M/2);
  r2=floor(N/2);
  d0=[20 40];
  n=2;
  for i=1:2
      for x=1:M
          for y=1:N
              d=sqrt((x-r1)^2+(y-r2)^2);
              h=exp(-0.5*(d/d0(i))^n);
              g(y,x)=h*FImage(y,x);
          end
      end
      g=real(ifft2(ifftshift(g)));
      subplot(1,3,i+1),
      imshow(uint8(g)),
      title(['指数低通滤波D0=',num2str(d0(i))]);
  end
  

• 结果：

1.2.3 梯形

• 编程思路：

  （1）读取原始图像，对图像进行灰度化处理。

  （2）用imnoise(Image,'gaussian')添加高斯噪声

  （3）通过fftshift(fft2(double(Image)))计算傅里叶谱，并傅里叶变换的结果进行平移，得到移位频谱图。

  （4）对图像进行指数低通滤波处理。

  （5）对滤波后的频谱进行反傅里叶变换，得到滤波后图像。

• 源代码：

  Homework1_2_3.c

  %利用傅里叶变换实现频域梯形低通滤波
  close all;
  clear;
  clc;
  Image=rgb2gray(imread('img.jpg'));         %读取原图转变为灰度化图像
  Image=imnoise(Image,'gaussian');           %添加高斯噪声
  subplot(1,3,1),imshow(Image),title('原图');%添加噪声后的原图
  FImage=fftshift(fft2(double(Image)));      %傅里叶变换及平铺搬移
  [N,M]=size(FImage);
  g=zeros(N,M);
  r1=floor(M/2);r2=floor(N/2);
  d0=[5 30];d1=[45 70];
  for i=1:2
      for x=1:M
          for y=1:N
              d=sqrt((x-r1)^2+(y-r2)^2);
              if d>d1(i)
                  h=0;
              else
                  if d>d0(i)
                      h=(d-d1(i))/(d0(i)-d1(i));
                  else
                      h=1;
                  end
              end
              g(y,x)=h*FImage(y,x);
          end
      end
      g=real(ifft2(ifftshift(g)));
      subplot(1,3,i+1),
      imshow(uint8(g)),
      title(['梯度低通滤波D0 = ',num2str(d0(i)),',D1 = ',num2str(d1(i))]);
  end
  

• 结果：

• 分析：

  （1）随着域的不同，对同一个事物的了解角度也随之改变，因此在时域某些不好处理的地方，在频域就可以较为简单的处理。同时，可以从频域里发现一些原先不易察觉的特征。

  （2）低通滤波就是保留图像中的低频成分，过滤高频成分。想要低通过滤器，就是要将高频区域的信号全部拉黑，而低频区域全部保留。低通滤波器是指通过低频的滤波器，衰减高频而通过低频，常用于模糊图像。低频滤波器与高通滤波器相反，当一个像素与周围像素的插值小于一个特定值时，平滑该像素的亮度，常用于去噪和模糊化处理。

  （3）不同的滤波方法在处理含有不同噪声的图像有不同的效果。更改参数，会产生微小变换。

  （4）对于各参数的分析

  • d0表示截止频率。
  • n表示的是滤波器的阶数，控制曲线的衰减速度。由于n的影响图像平滑程度，导致不同滤波器产生的振铃效应不同，更改n，会产生微小变换。
  • 随着阶数n的增加，振铃效应会越来越明显。

  （5）三种方法的对比

  • 低通滤波器滤除了高频成分，所以使得图像模糊。由于理想低通滤波器的过度特性过于急峻，会产生了振铃现象。
  • 巴特沃斯低通滤波对噪声的平滑效果不如理想低通滤波，采用该滤波器在抑制噪声的同时，图像边缘的模糊程度大大减小，振铃效果不明显。
  • 指数低通滤波没有振铃现象。
  • 梯形低通滤波与指数低通滤波器相比较，滤波输出图像有一定的模糊和振铃效应。

2. 图像的几何变换

2.1 教材-例3.1

【例3.1】基于 MATLAB编程,采用反向映射法实现图像平移,分别沿x轴、y轴平移20个像素。

• 编程思路：

  （1）以原图像的尺寸创建一个新图像并将其初始化。

  （2）将新图像的每个点赋值。

  ​ 循环扫描新图像（平移后的图像）的每一个点，该点的取值为该点的坐标减去平移量所在坐标的值。

  ​ 即为：oldx=x-deltax; oldy=y-deltay;

  ​ NewImage(y,x,:)=Image(oldy,oldx,:);

• 源代码：

  Homework_2_1.m

  %【例3.1】基于 MATLAB编程,采用反向映射法实现图像平移,分别沿x轴、y轴平移20个像素。
  close all;
  clear;
  clc;
  Image=im2double(imread('img.jpg'));               %读取图像并转化为double型
  [h,w,c]=size(Image);                              %获取图像尺寸
  NewImage=ones(h,w,c);                             %新图像初始化 
  deltax=20;deltay=20;                              %指定平移量
  for x=1:w
      for y=1:h                                     %循环扫描新图像中的点
          oldx=x-deltax;
          oldy=y-deltay;                            %确定新图像中的点在原图中的对应点
          if oldx>0&&oldx<w&&oldy>0&&oldy<h         %判断对应点是否在图像内
              NewImage(y,x,:)=Image(oldy,oldx,:);   %赋值
          end
      end
  end
  subplot(1,2,1),imshow(Image),title('原图');        %原图
  subplot(1,2,2),imshow(NewImage),title('平移后的图');%平移后的图 
  

• 结果：

• 分析：

  （1）对原图像的中的每一个像素点进行该变换（仅仅是位置变换），得到新的坐标，然后在新坐标下显示原图像。

  ​ 循环扫描新图像（平移后的图像）的每一个点，该点的取值为该点的坐标减去平移量所在坐标的值。

  ​ 即为：oldx=x-deltax; oldy=y-deltay;

  ​ NewImage(y,x,:)=Image(oldy,oldx,:);

  ​ 由结果可看到图像已经分别沿x轴、y轴平移。

2.2 教材-例3.6

【例3.6】基于 MATLAB编程,实现图像放大,比例为kx=1.5,ky=1.5，分别采用最邻近插值和双线性插值方法生成放大后的图像。

• 编程思路：

  （1）用Image=im2double(imread('img.jpg')); 读取图像。

  （2）使用imresize()函数进行放大。

  （3）将放大的图像显示出来，为了便于观察特别显示其坐标值，能够表明图片已经放大。

• 源代码：

  Homework_2_2.m

  %【例3.6】基于 MATLAB编程,实现图像放大,比例为kx=1.5,ky=1.5，分别采用最邻近插值和双线性插值方法生成放大后的图像。
  close all;
  clear;
  clc;
  Image=im2double(imread('img.jpg'));                      %读取图像并转化为double型
  NewImagel = imresize(Image,1.5,'nearest');               %比例为1.5最临近插值方法放大
  NewImage2 = imresize(Image,1.5,'bilinear');              %比例为1.5双线性插值方法放大
  subplot(1,3,1),imshow(Image),title('原图'),axis on;              %原图
  subplot(1,3,2),imshow(NewImagel),title('最临近插值方法'),axis on;%最临近插值方法放大图
  subplot(1,3,3),imshow(NewImage2),title('双线性插值方法'),axis on;%双线性插值方法放大图
  

• 结果：
  

• 分析：

  （1）使用imresize()函数，第一个参数为所处理的图片，第二个是放大的比例，第三个选择方式。

  • `imresize(Image,1.5,‘nearest’)代表比例为1.5最临近插值方法放大
  • imresize(Image,1.5,'bilinear')代表比例为1.5双线性插值方法放大

  （2）因为一起显示的原因看着好像长宽相同，但是通过坐标轴可以看到长款均已是原图的1.5倍。

  （3）因将截图放入文档，图片有些许缩小，在实验时放大图片可以看到最邻近插值图像中有明显的锯齿状，而双线性内插结果图中比较光滑，也带一点模糊的感觉。仔细观察结果图片可以看出。

2.3 教材-例3.7

• 编程思路：

  （1）使用maketform()函数和imtransform()进行操作。

  （2）采用最邻近插值和双线性插值方法生成比例为dx=0.5,dy=0.5,错切后的图像。

• 源代码：

  Homework_2_3.m

  %【例3.7】基于 MATLAB编程,实现图像错切,比例为dx=0.5,dy=0.5,分别采用最邻近插值和双线性插值方法生成错切后的图像。
  close all;
  clear;
  clc;
  Image=im2double(imread('img.jpg'));                              %读取图像并转化为double型
  tform1=maketform('affine',[1 0 0; 0.5 1 0;0 0 1]);
  tform2=maketform('affine',[1 0.5 0;0 1 0 ;0 0 1]);
  NewImagel= imtransform(Image,tform1);
  NewImage2= imtransform(Image,tform2); 
  subplot(1,3,1),imshow(Image),title('原图');                       %原图
  subplot(1,3,2),imshow(NewImagel),title('最临近插值方法错切后的图像'); %最临近插值方法错切后的图像
  subplot(1,3,3),imshow(NewImage2),title('双线性插值方法错切后的图像'); %双线性插值方法错切后的图像
  

• 结果：

• 分析：

  （1）maketform()函数用于创建空间变换结构，变换类型为‘affine’，代表二维或 N 维仿射变换。

  （2）图像的错切变换是平面景物在投影平面上的非垂直投影。错切使图像中的图形产生扭变。这种扭变只在水平或垂直方向上产生时,分别称为水平方向上的错切和垂直方向上的错切。错切之后原图像的像素排列方向发生改变。导致图像发生了扭曲。得到的结果左图为水平错切，右图为垂直错切。

2.4 教程例3.9

• 编程思路：

  （1）读取前景图和背景图。

  （2）使用imabsdiff(a,b)函数计算a,b两个uint8数组的绝对差。

• 源代码：

%【例3.9】基于 MATLAB编程实现两幅图像相减。
close all;
clear;
clc;
Back = imread('hallback.jpg');                     %读取背景图
Foreground = imread('hallforeground.jpg');         %读取前景图
result1 = imabsdiff (Back,Foreground);             %两个uint8数组之间的绝对差
subplot(1,3,1), imshow(Back),title('背景图');       %显示背景图
subplot(1,3,2), imshow(Foreground),title('前景图'); %显示前景图
subplot(1,3,3), imshow(result1),title('图像相减');  %显示图像相减后的图

• 结果：

• 分析：

  （1）Z = imabsdiff(X,Y) %计算X和Y像素之差的绝对值

  （2）此运算可以显示两幅图像的差异，检测同一场景两幅图像之间的变化，去除不需要的背景，得到了樱桃小丸子的图像。

2.5 教程例3.12

• 编程思路：

  （1）读取背景图和蝴蝶图片。

  （2）定义要随机变换多少只，然后用for循环一次变化。

  （3）定义变换的方式，用randi(6, 1, 3)代表在缩小、旋转、三种镜像及错切六种几何变换中随机选择三种，然后依次进行变换。

  （4）将变化的后的蝴蝶与背景图进行叠加。

  （5）给出效果图。

• 源代码：

  %【例3.12】有一幅蝴蝶的图片和一幅风景图片,试基于 MATLAB编程,基于几何、代数和色彩通道运算,实现漫天蝴蝶飞舞的合成图像。
  close all;
  clear;
  clc;
  Image = imread('butterfly.png');
  Back = imread('背景图.jpg');
  subplot(131), imshow( Image), title('蝴蝶');
  subplot(132), imshow(Back),title('背景');
  [h,w,c] = size(Back);
  population = 20;                  %随机变化出20只蝴蝶
  num=3;                            %拟进行三种几何变换
  for k= 1: population
      type = randi(6, 1, num);      %在缩小、旋转、三种镜像及错切六种几何变换中随机选择三种
      NewImage = Image;
      for n = 1 : num
          switch type(n)
              case 1  %比例变换
                  scale = rand();
                  %缩小比例随机生成
                  NewImage = imresize( NewImage, scale,'bilinear');
                  %缩小变换,双线性插值
              case 2  %旋转变换
                  angle = round(rand()*100);
                  %逆时针旋转角度随机生成
                  NewImage = imrotate( NewImage, angle,'bilinear');
                  %为旋转变换,双线性插值
              case 3  %错切变换
                  shear = rand()/2; %错切系数0~0.5
                  tform1 = maketform('affine',[1 0 0; shear 1 0;0 0 1]);
                  tform2 = maketform('affine',[1 shear 0; 0 1 0;0 0 1]);
                  NewImage = imtransform(NewImage, tform1);
                  NewImage = imtransform(NewImage, tform2);
              case 4  %水平镜像
                  NewImage = flipdim( NewImage,2);
              case 5  %垂直镜像
                  NewImage = flipdim(NewImage,1);
              case 6  %对角镜像
                  NewImage = flipdim(NewImage,2);
                  NewImage = flipdim(NewImage,1);
          end
      end
      [newh,neww,newc] = size(NewImage);
      positionx = randi(w-2 * neww,1,1);
      positiony = randi(h-2 * newh,1,1);  %叠加位置
      temp = Back(positiony:positiony+newh-1,positionx:positionx+neww-1, : );
      colorchange = randi(3, 1, 2);
      if colorchange(1) ~= colorchange(2)
          color = NewImage (:,:, colorchange (1));
          NewImage (: ,: ,colorchange(1)) = NewImage (: ,: ,colorchange(2));
          NewImage(:,:, colorchange(2)) = color;
      end  %色彩通道交换
      C = NewImage(:,:,1)& NewImage(:,:,2)&NewImage(:,:,3);
      pos = find(c(:)==0);
      NewImage(pos) = temp(pos);
      NewImage(pos+newh*neww) = temp(pos+newh*neww);
      NewImage(pos+2*newh*neww) = temp(pos+2* newh*neww);
      %去除几何变换中产生的背景黑色点
      temp= NewImage;
      Back(positiony: positiony+newh- 1, positionx: positionx+neww-1,: )=temp; %叠加
  end
  subplot(133), imshow(Back), title('合成图');
  

• 结果：

• 分析：

  （1）基于几何、代数和色彩通道运算，前面都有涉及与解释。主要考虑整个逻辑的设计。

  （2）此代码还有优化的空间，虽然蝴蝶原图片背景底色为透明，但好像识别不出来，最终将其合并在一起时有突兀的黑色背景。应当进行优化。如将图片叠加起来是可以自己写一个函数，如果识别出该像素点为黑色可以不进行叠加。

3. 图像的边缘检测

3.1 比较拉普拉斯算子、LOG算子、Canny算子三种边缘检测算法

• 编程思路：

  （1）读取二通道灰度图片并将其转化为double型。im2double(rgb2gray(imread('img.jpg')))

  （2）分别用三种方放进行边缘检测

• 源代码：

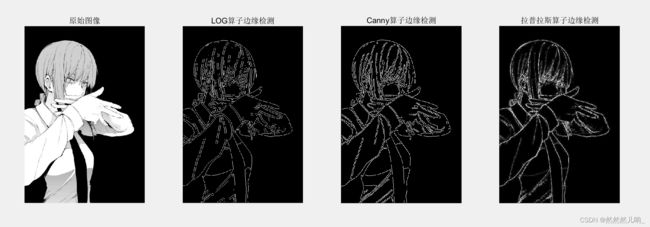
  % 3.1 比较拉普拉斯算子、LOG算子、Canny算子三种边缘检测算法
  close all; 
  clear; 
  clc;
  Image=im2double(rgb2gray(imread('img.jpg')));     %读取图像并转化为double型
  
  % LOG算子
  BW1= edge( Image,'log');                          %使用LOG算子进行边缘检测,得到二值边界图像
  H1= fspecial('log',7,1);                          %生成7X7的LOG模板,标准差为1
  R1= imfilter( Image, H1);                         %LOG算子滤波
  edgeImage1 = abs(R1) ;                            %生成LOG滤波图像
  sharpImage1 = Image + edgeImage1;                 %锐化图像
  
  % Canny算子
  BW2= edge( Image, 'canny');                       %使用Canny算子进行边缘检测,得到二值边界图像
  
  % 拉普拉斯算子
  [M,N]=size(Image);
  BW3=zeros(size(Image));
  for x=2:M-1
      for y=2:N-1
          BW3(x,y)=abs(Image(x+1,y)+Image(x-1,y)+Image(x,y+1)+Image(x,y-1)-4*Image(x,y));
      end
  end
  I=im2uint8(Image);
  BW3=im2uint8(BW3);
  % 显示结果
  subplot(1,4,1),imshow(Image), title('原始图像');
  subplot(1,4,2),imshow(BW1), title('LOG算子边缘检测');
  %subplot(1,8,3),imshow(edgeImage1), title('LOG滤波图像');
  %subplot(1,8,4),imshow(sharpImage1), title('LOG锐化图像');
  subplot(1,4,3), imshow(BW2), title('Canny算子边缘检测');
  subplot(1,4,4), imshow(BW3), title('拉普拉斯算子边缘检测');
  

• 结果

• 分析

  （1）在空域运算中来说，对图像的锐化就是计算微分。由于数字图像的离散信号，微分运算就变成计算差分或梯度。通过计算梯度，设置阈值，得到边缘图像。

  （2）算子分析

  • 拉普拉斯算子属于空间锐化滤波操作，是二阶微分线性算子。在图像边缘处理中，二阶微分的边缘定位能力更强，锐化效果更好，因此在进行图像边缘处理时，直接采用二阶微分算子而不使用一阶微分。
  • LoG算子，即高斯-拉普拉斯算子，是一个二阶导数算子。它的原理是先对图像进行高斯模糊，然后再求二阶导数，二阶导数等于0处对应的像素就是图像的边缘。
  • Canny 算子的原理是用高斯滤波器平滑图像，再用一阶偏导有限差分计算梯度幅值和方向，然后对梯度幅值进行非极大值抑制，最后用双阈值算法检测和连接边缘。

  （3）整体分析

  • LOG 和 Canny 算子检测出的边缘比较连贯，且具有较好的平滑性，边缘细节也更多。相比之下拉普拉斯算子检测出的边缘细节较少，边缘较模糊。从结果图上看，边缘提取效果 Canny > LOG > Laplace。

  （4）拓展：经过查资料得知还有Roberts 算子、Prewitt 算子和Sobel 算子。

  • Roberts 算子可以得到非常细的边缘，定位的精度很高，能够检测到的边缘较少，最大的优点是计算量小速度快，适用于边缘明显且噪声较少的图像分割。
  • Prewitt 算子和 Sobel 算子检测出的结果类似，相比之下 Sobel 检测的边缘更加突出。