Apollo EM Planner阅读笔记

论文地址：https://arxiv.org/abs/1807.08048
论文类型：Motion Planning

目录：

简介

EM Planner是Apollo面向L4的实时运动规划算法，该算法首先通过顶层多车道策略，选择出一条参考路径，再根据这条参考线，在Frenet坐标系下，进行车道级的路径和速度规划，规划主要通过Dynamic Programming和基于样条的Quadratic Programming实现。EM Planner充分考虑了无人车安全性、舒适性、可扩展性的需求，通过考虑交通规则、障碍物决策、轨迹光滑性等要求，可适应高速公路、低速城区场景的规划需求。通过Apollo仿真和在环测试，EM Planner算法体现了高度的可靠性，和低耗时性。

多车道EM Planner框架

整体框架

所有规划需要的信息在EM Planner的顶层汇集，然后参考线生成器会生成一些基于障碍物和交通规则的候选车道级参考线，这个过程主要是依赖于高精度地图和Routing模块给出的全局规划结果。以下是车道级的规划过程：

1. 首先会基于给定参考线生成Frenet坐标系，通过给定参考线将所有的自车信息和环境信息转换到参考线下的Frenet坐标系。
2. 接下来所有的车道级信息将会传递给车道级最优求解器，该求解器会求解最优路径和最优速度。在求解最优路径时，周围环境信息将会被投影到Frenet坐标系（E-step），然后基于投影的信息生成一条光滑路径（M-step）。
3. 同样的，在求解最优速度时，一旦生成了一条最优路径，障碍物就会被投影到ST图中（E-step），然后最优速度求解器会生成一条光滑的速度规划（M-step）。结合路径和速度规划结果，就生成了一条给定车道的光滑轨迹。
4. 最后一步会将所有的车道级轨迹传递给参考线轨迹决策器，基于当前车辆状态、相关约束和每条轨迹的代价，轨迹决策器会决定一条最优的轨迹。

多车道策略

利用搜索算法【2】【3】结合代价估算形成变道策略是一种比较常见的处理变道问题的方法，但是这种方法存在计算量大、难以适用交规以及前后决策可能缺少连贯性等特点。Apollo的解决办法是将多车道策略划分为两种类型：无法通行的被动变道，和能够通行的主动变道。被动变道一般由道路阻挡造成的，通过全局规划模块重新生成全局路径解决；主动变道是考虑动态障碍物而做出的决策。Apollo通过同步生成多条候选车道的方法解决主动变道问题，在Frenet坐标系下，投影障碍物、考虑交规后生成多条车道级的候选路径，最后传递到变道决策器中选择出一条最优的车道决策

路径-速度迭代算法

在Frenet坐标下的轨迹规划实际上带约束的3D最优求解问题。该问题一般有两种求解方法：直接3D最优化求解和路径-速度解耦求解。直接方法【4】【5】试图在SLT坐标系下使用轨迹采样或Lattice搜索,这些方法都受到搜索复杂度的限制，因此搜索结果是次优的。而路径-速度解耦规划会分别求解路径和速度的最优解。速度的生成将会在生产的路径上进行【6】。虽然结果可能也不是最优的，但会在速度和路径分别求解时更加灵活。
EM Planner迭代地进行路径和速度最优求解，通过估计和来向、低速障碍物的交互，上一帧的速度规划将有助于下一帧的路径规划。然后将路径规划结果再交给速度最优求解器来推算出一个最优的速度结果。

决策和交通规则约束

交通规则是硬约束，而与障碍物的交互是软约束。一些决策方法直接考虑的是数值上的最优解【7】，也有像【5】一样同时进行规划和决策。而Apollo EM Planner的决策是优先于规划的，决策模块将会为规划带来更明确的意图，减少最优求解的搜索空间。决策部分的第一步是将车辆的运动意图用一根粗略、灵活的轨迹来描述。这条轨迹也可以用来估计与障碍物之间的交互，并且当情景更加复杂时，这种基于轨迹的决策方法也是灵活的。第二步是基于决策生成的轨迹来构造一个凸空间，用来做基于样条光滑的轨迹生成，主要是通过二次规划来达到迭代生产路径、速度解的目的。

车道级EM PLanner框架

整体框架

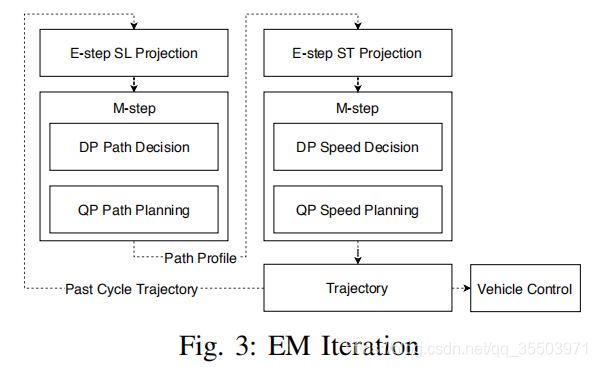
框架包括了一帧规划中的两个E-step和两个M-step，轨迹信息将会在前后两帧中传递，以下是整个车道级规划的流程：

1. 在第一个E-step中，障碍物会被投影到车道Frenet坐标系，障碍物包括了静态障碍物和动态障碍物。静态障碍物会直接从笛卡尔坐标系转换到Frenet坐标系，而动态的信息则以其运动轨迹来描述。通过上一帧的预测信息，和自车的运动信息，可以估算自车和动态障碍物在每个时间点的交互情况，轨迹重叠的部分会被映射到Frenet坐标系中。初次之外，在最优路径求解过程中，动态障碍物的出现会最终导致自车做出避让的决策。因此，出于安全的考虑，SL投影只考虑低速和来向障碍物，而对于高速的动态障碍物，EM Planner的平行变道策略会考虑这种情景。
2. 在第二个E-step，所有的障碍物都会在ST中与生成的速度信息进行估计，如果对应的ST中重叠部分，那么对应区域将会在ST中进行重新生成。
3. 在两次M-step过程中，通过Dynamic Programming和Quadratic Programming生成路径和速度规划。然而在进行投影的SL和ST坐标内求解时非凸的，因此，为了解决这个问题，首先使用Dynamic Programming获得一个粗略的解，同时这个解也能够提供诸如避让、减速、超车的决策。通过这个粗略的解，可以构建一个凸的通道，然后使用基于Quadratic Programming的样条最优求解。

接下来的部分将会详细介绍框架中的步骤。

SL和ST投影（E-step）

SL投影

SL投影是基于类似于【3】中的G2光滑参考线（曲率导数连续）。给定一个时刻，如果自车与预测的障碍物轨迹有重叠区域，那么这个重叠区域将会在SL坐标系被标注为与动态障碍物的估计交互区域。这个区域可以理解为自车和动态障碍物的包围盒的重叠区域。图4展示了这一种案例，红色代表动态障碍物的预测轨迹，用离散点来表示；蓝色表示自车的状态。

ST投影

ST投影用于帮助我们估计自车的速度规划。当生成了一条光滑的路径以后，与自车有交互的动态障碍物和静态障碍物都会被投影到路径上，同理，这种交互也定义为包围盒的重叠。如图5，这是一个ST图投影案例。

红色区域表示在2s处距离自车40m远切入规划路径的动态障碍物ST信息，绿色表示在自车后的动态障碍物ST信息，M-step将会在剩下的区域找到可行光滑最优解。

DP路径（M-step）

M-step求解Frenet坐标系下的最优路径规划，实际上在一个非凸的区间（从左和从右避让是两个局部最优情景）就是找到一个最优的$l=f(s)$方程。主要包括两步：基于Dynamic Programming的路径决策和基于样条的路径规划。

基于Dynamic Programming的路径步骤提供一条粗略的路径信息，其可以带来可行通道和绕障决策，如图6所示，这一步包括Lattice采样、代价函数、Dynamic Programming搜索。

Lattice采样基于Frenet坐标系，多行的点在撒在自车前。如图7所示，行与行之间的点使用五次方多项式连接，而行与行之间的间隔取决于自车速度、道路结构、是否换道等等。出于安全考虑，路径总长可以达到200m或者覆盖8s的行驶长度。

每段Lattice路径的代价通过光滑程度、障碍物避让、车道代价来评价：

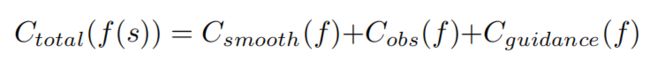
而光滑程度又通过以下方程来衡量，一阶导表示朝向偏差，二阶导表示曲率，三阶导表示曲率导数：

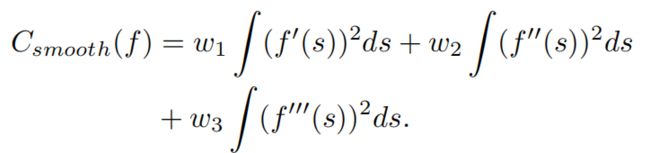
障碍物的代价由以下方程给出，方程中的d由自车bounding box到障碍物bounding box的距离表示。

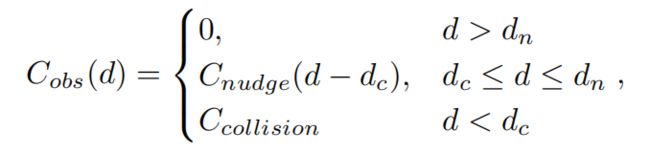
车道代价由以下方程给出，主要是考虑在道路上与否以及与参考线之间的差异，一般是与车道中心线的差异：

样条QP路径（M-step）

基于样条的路径可以理解为是Dynamic Programming更精细的版本。通过DP采样出的路径生成一条可通行通道，然后在通道中利用基于Quadratic Programming的样条曲线生产光滑路径。具体实例如图8所示，步骤流程可由图9所示：

QP的目标函数为：

其中$g(s)$为DP规划的路径，$f(s)$的一阶导表示朝向、二阶导表示曲率、三阶导表示曲率的导数。该函数描述了避让障碍物和曲线光滑性之间的权衡。

QP的约束包括边界约束和动力学可行性。这些约束都会施加在每个s处，通过限制l来将车辆限制在车道内。由于EM Planner使用的是自行车模型，因此这样对l的限制也是不够的。如图10所示，为了使得边界约束变凸并且线性，在自车的前后两端各增加了一个半圆。前轮到后轮中心的距离用$l_f$表示，车宽用w表示，因此车的左前角的横向位置可以用以下方程给出：

通过线性化可以变为：

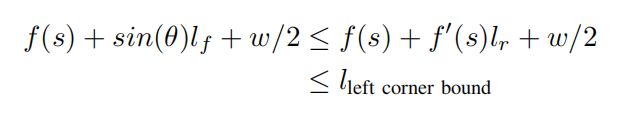
同理，其余三个角的位置都可以被线性化，显然因为$\theta$足够小，小于pi/12，因此可以这样线性化。

$f(s)$的二阶导和三阶导与动力学可行性相关，除了边界条件以外，生成的路径还应该和自车的初始条件相匹配。因为所有的约束都是线性的，所以使用Quadratic Programming求解非常迅速。

具体的光滑样条曲线和QP问题可以在附录中查阅。

DP速度求解（M-step）

M-step的速度规划是在ST图中求解最优速度规划，即求解出最优函数$S(t)$。与求解最优路径相似，在ST图中求解最优速度规划也是非凸的最优化问题。同样也采用Dynamic Programming配合样条曲线Quadratic Programming来找到光滑速度规划。图12是速度求解的pipeline：

DP速度求解包括代价函数、ST栅格图以及Dynamic Programming搜索。生成的结果包括分段线性的速度规划、可通行通道以及障碍物速度决策。如图11所示，该结果在QP中用来作为参考速度规划，通过该参考速度生成凸的区域。

在栅格图中，使用有限差分法来估计速度、加速度和jerk：

从DP生成的速度中选择出最优的一条的方法是最小化以下的代价函数：

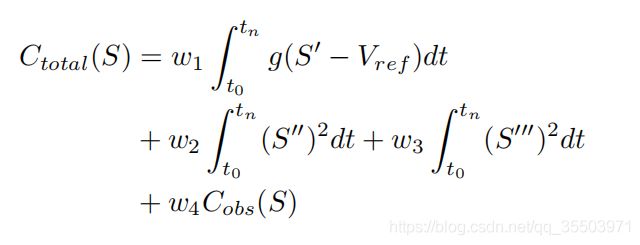
第一项是速度误差，g用来惩罚与$V_{r}ef$的不同的误差。第二项、第三项用来描述曲线的光滑程度。最后一项用来描述障碍物代价，以到障碍物的距离来衡量。

DP搜索空间也收到车辆动力学约束，并且也有单调性约束，因为不希望车辆倒退。一些对于动力学约束的必要简化也用来加速算法。

QP速度求解（M-step）

因为分段线性的速度规划不能满足动力学的要求，所以需要使用Quadratic Programming来填补动力学空缺。图13是样条曲线QP速度求解的pipeline：

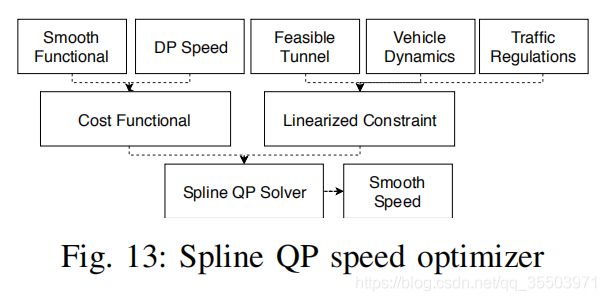
QP速度求解包括三部分：代价函数、线性约束以及样条曲线QP求解器。
除了初始条件约束以外，主要有以下的边界约束：

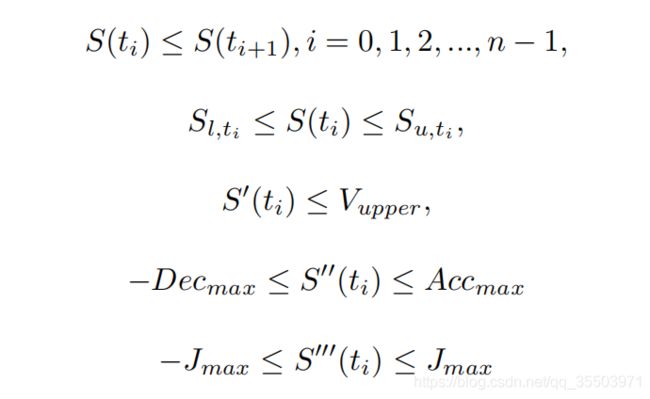
第一个约束是单调性约束；第二、第三、第四约束主要是交通规则和车辆动力学约束。通过约束、cost函数计算以后，spline QP speed会生成一条如图14中的光滑可行的速度规划。

结合路径规划，EM Planner最终会生成一条光滑轨迹。

解QP问题的说明

为了安全考虑，路径和速度大概在100个不同的位置或时间点，那么约束就有超过600个。对于速度、路径求解，分段五次多项式已经足够，因此样条曲线大概有3-5个多项式，大概就有30个参数。因此Quadratic Programming就变成了相对小的目标函数，和相对大的约束。QP能比较好的解决这个问题，并且使用了上一帧的解作为热启动，加速求解过程。实践中，QP问题解的平均时间3ms。

DP和QP非凸问题的说明

在非凸问题上，DP和QP都有他们单独的限制。DP和QP的组合，能够很好吸收两者优点，并求得一个理性解。

• DP:DP的优劣受到撒点分辨率和时间分辨率的影响，通常在运行时间限制的情况下，一般只会得出一个粗糙解而非最优解，比如会从障碍物左侧绕开，但并不是按照最完美的路径绕开。
• QP:QP需要在凸空间求解，因此必须借助DP的解来形成凸空间。随机的或者基于规则的决策，通常会给QP带来非凸的空间，因此解QP问题会失败或者陷入局部最优。
• DP+QP:（1）通过DP寻求粗糙解；（2）DP解能够生成凸空间；（3）QP在DP解形成的凸空间内，很大可能能够获得全局最优解。

案例分析

图15展示了EM Planner在规划周期内，帧与帧之间完成最优轨迹规划的过程。

假设自车以10m/s的速度行进，一动态障碍物沿着相反方向朝着我们以同样10m/s的速度驶来，EM Planner按以下步骤迭代生成速度和路径规划：

1. 历史规划（图15-a）：在动态障碍物出现之前，自车以恒定速度10m/s向前行驶。
2. 路径规划迭代1（图15-b）：基于当前车速和动态障碍物的车速，两者将会在S=40m处相遇，因此，最好的方法是在S=40m处绕开障碍物。
3. 速度规划迭代1（图15-c）：基于路径规划结果，即从右侧避开障碍物，自车将调整其速度规划，在避开障碍物之前减速到5m/s。
4. 路径规划迭代2（图15-d）：由于产生了新的速度规划，自车将不再会与动态障碍物在S=40m处避开，而会在一个新的位置S=30m处避开障碍物。因此，路径规划结果也将会随速度规划改变而重新更新。
5. 速度规划迭代2（图15-e）：由于路径规划已经更新，新的绕障位置在S=30m处，因此在S=40处减速也就没有必要了，新的速度规划使得自车可以在S=40m处加速而在S=30m处形成一个光滑的绕障。

经过迭代之后，最终车辆将在S=30m处减速绕障，并且绕障结束之后会加速，这样一个过程和人类驾驶员的表现很相似。
但值得注意的是，并不是每次规划都必须采取如上四步骤，根据场景不同可能会产生更多或更少的步骤。一般而言，场景越复杂，所需要的步骤就越多。

总结

EM Planner是一种基于弱决策的算法，相比于强决策算法，EM Planner在复杂场景、多障碍物情况下表现更好。强决策依赖于提前制定出的决策行为，并且有难以理解和预测与障碍物交互的缺陷、难以满足大量障碍物阻挡生成基于规则的最佳轨迹的缺陷。
EM Planner通过将三维规划问题转化为两个二维规划问题，显著地降低了运算复杂度，因此会带来运行时间的压缩和整个系统的可交互性。