图解 Pytorch 中 nn.Conv2d 的 groups 参数

普通卷积复习

首先我们先来简单复习一下普通的卷积行为。

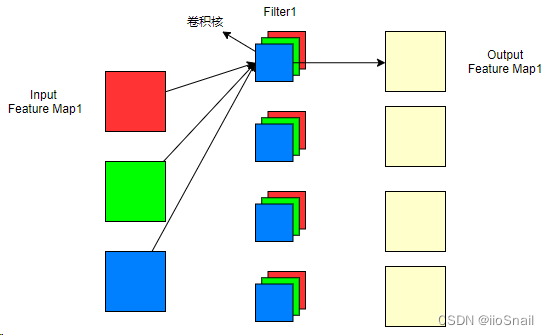
从上图可以看到，输入特征图为3，经过4个filter卷积后生成了4个输出特征图。对于普通的卷积操作，我们可以得到几个重要的结论：

1. 输入通道数 = 每个filter的卷积核的个数。（注意区分卷积核和Filter，它们俩的关系是：多个卷积核组成一个Filter）
2. Filter的个数 = 输出通道数

此时，我们的参数量为：

$$\text{参数量}=输入通道数\times 输出通道数\times 卷积核大小=卷积核个数\times \text{Filter数 }\times 卷积核大小$$

这里忽略了偏置

Groups是如何改变卷积方式的

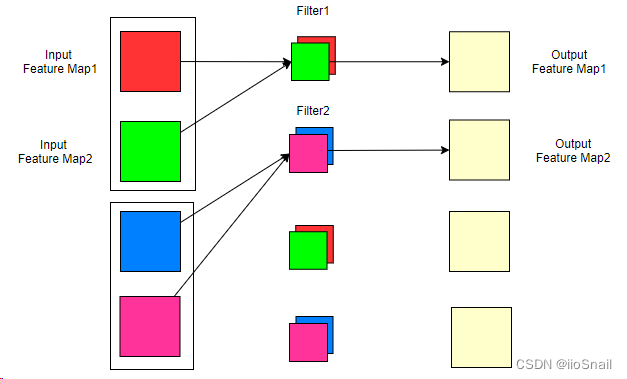
那现在我们不想按照上面的方式，我想让一个Filter只负责一部分输入通道，例如：

上图中，我们将输入通道分成了2组（也就是groups=2），每一组对应一个Filter，这样我们的参数量就下降了1倍。此时，我们还是有4个Filter（因为有4个输出通道），但每个Filter只有2个卷积核，所以一个Filter只对2个输入通道进行卷积。

为了巩固，我们再举个例子：

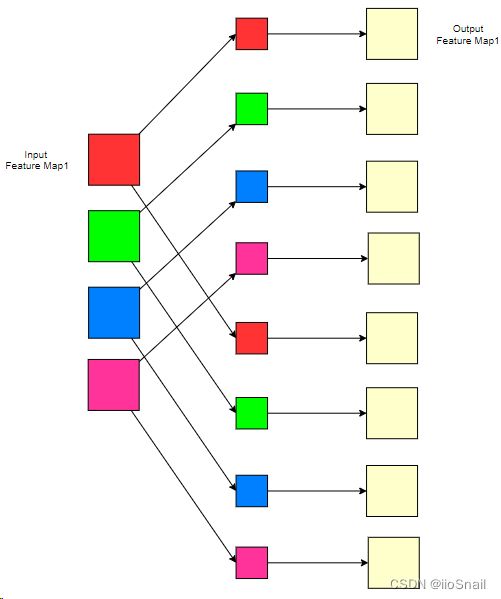
在该例子中，我们的输入通道为4，输出通道为8。这次我们将4个输入通道分成了4组，也就是groups=4，此时我们的每个Filter的卷积核数量就是1。

从上面两个例子，大家应该很清楚group的作用了，这里进行一个总结：

1. Groups做的事情：将输入通道进行分组，groups的值就是具体分的组数。所以，in_channel ÷ groups 一定要是整数，要不然就没法分组了。每个Filter负责处理一组输入通道，所以Filter的卷积核数量也会随之改变，即每个Filter的卷积核数 = in_channel ÷ groups
2. Groups的作用：减少计算量和参数量。
3. Groups其他注意事项：输出通道 ÷ groups 也一定要是整数，要不然就会有几组没有Filter与之对应了。

综上，如果加入了groups，则卷积参数量的计算公式为：

$$\text{参数量}=\frac{\text{输入通道数}}{groups}\times 输出通道数\times 卷积核大小$$

这里同样忽略了偏置

实验验证

我们现在就来做一组实验，验证上面的说法。 这里我准备一个1x1的图片，卷积核大小也为1x1，输入通道数为4， 输出通道数为8，groups设为2。用图像表示则为：

实验开始：

首先，我们先导包和准备一个打印参数数量的辅助函数：

import torch.nn as nn
import torch

def get_parameter_number(net):
    total_num = sum(p.numel() for p in net.parameters())
    return {'Total': total_num}

接下来定义卷积模型，并打印参数量：

model = nn.Conv2d(4, 8, 1, 1, groups=2, bias=False)
get_parameter_number(model)

{'Total': 16}

可以看到，参数量和预期的是一致的。8个Filter，每个Filter两个卷积核，所以一共16个参数。

接下来定义输入层，输入层是1x1的图片，值都为1：

inputs = torch.ones(1, 4, 1, 1)

然后修改卷积核的参数，改为图片上的[1,2,3,4…,16]：

for param in model.parameters():
    print(param.size())
    param.data = torch.FloatTensor([list(range(1, 17))]).view(8,2,1,1)

torch.Size([8, 2, 1, 1])

通过参数的shape也可以看出来，8个filter，每个filter2个卷积核。接下来进行前向传递：

model(inputs)

tensor([[[[ 3.]],
         [[ 7.]],
         [[11.]],
         [[15.]],
         [[19.]],
         [[23.]],
         [[27.]],
         [[31.]]]], grad_fn=)

完美，跟预想中的结果完全一致。

参考资料

https://pytorch.org/docs/stable/generated/torch.nn.Conv2d.html