玩链子游戏

一 游戏描述

有一条链子，上面有 n 颗钻石，钻石编号为 1～n 。可以对该链子执行两种操作：

① CUT a b c （区间切割操作）

切下从第 a 颗钻石到第 b 颗钻石的链子，把它插在剩余链子的第 c 颗钻石后面；比如 n 等于8，链子是 1, 2, 3, 4, 5, 6, 7, 8，对该链子执行 CUT 3 5 4，会切下 3, 4, 5 链子，剩下 1, 2, 6, 7, 8 链子，把 3, 4, 5 链子插入第 4 颗钻石之后，现在的链子是 1, 2, 6, 7,3, 4, 5, 8；

② FLIP a b （区间反转操作）

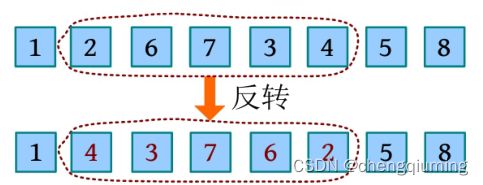
切下从第 a 颗钻石到第 b 颗钻石的链子，把链子倒过来放回原来的位置，比如在链子 1, 2,6, 7, 3, 4, 5, 8 上执行 FLIP 2 6，则得到的链子是1, 4, 3, 7, 6,2, 5, 8。那么执行 m 种操作后，链子的外观是怎样的呢？

二 输入

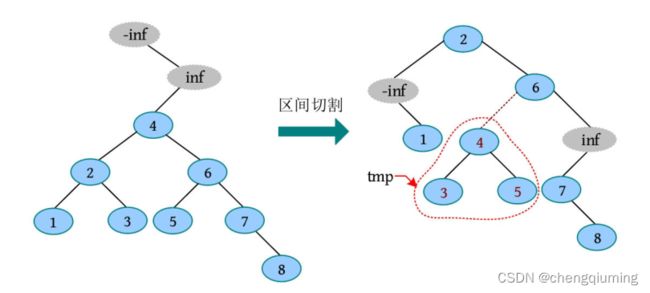
输入包括多个测试用例，在测试用例的第 1 行都输入两个数字 n 和 m（1≤n ，m≤3×10^5 ），分别表示链子的钻石总数和操作次数。接下来的 m 行，每行都输入 CUT a b c 或者 FLIP a b 。CUT a b c 表示切割操作，1≤a≤b≤n，0≤c≤n-(b-a +1)；FLIP a b 表示反转操作，1≤a

三 输出

对每个测试用例，都输出一行 n 个数字，第 i 个数字是链子上第 i 颗钻石的编号。

四 输入和输出样例

1 输入样例

8 2

CUT 3 5 4

FLIP 2 6

-1 -1

2 输出样例

1 4 3 7 6 2 5 8

五 分析

本游戏包括区间切割（CUT a b c ）、区间反转（FLIP a b）两种操作。这里以输入测试用例“8 2”进行分析，过程如下。

1 链子的初始状态如下

2 执行 CUT 3 5 4

切下从第 3 颗钻石到第 5 颗钻石的链子，把它插入剩余链子上第4颗钻石的后面。

3 执行 FLIP 2 6

切下从第 2 颗钻石到第 6 颗钻石的链子，把它倒过来放回原来的位置。

六 算法设计

1 创建伸展树，因为要进行区间操作，因此增加两个虚节点。

2 根据读入的信息，判断是执行区间切割操作还是区间反转操作。

3 按照中序遍历，输出伸展树。

七 图解

1 创建伸展树

数据序列为 1, 2, 3, 4, 5, 6, 7, 8，创建伸展树时在序列的首尾增加两个虚节点，该节点的值为无穷小 -inf，无穷大 inf（inf 是一个较大的数，如 0x3f3f3f3f）。由于在序列前面添加了一个虚节点，所以原来的位序增加 1，因此对 [l , r ]区间的操作变为对 [++l ,++r] 区间的操作。

2 区间切割

首先切割 [l , r] 区间，将 Al-1 旋转到根，然后将Ar +1 旋转到 Al -1 的下方，此时切割的 [l , r ] 区间是 Ar +1 的左子树，用 tmp 暂存。然后查找第 pos 个节点，可以将 Apos 旋转到根部，再将 Apos+1 旋转到 Apos 下方，将 tmp 挂接在 Apos+1 的左子树上即可，相当于将 [l,r ] 区间插入第 pos 个节点之后，如下图所示。

CUT 3 5 4：因为添加了虚节点，因此切割 [4, 6] 区间，将其插入剩余区间第 5 个节点的后面。将第 3个节点（数字2）旋转到根，然后将第 7 个节点（数字6）旋转到第 3 个节点的下方，此时切割的区间就是第 7 个节点的左子树，用 tmp 暂存。

然后将第 5 个节点旋转到根部，将第 6 个节点旋转到其下方，将 tmp 挂接在第 6 个节点的左子树上即可，此时序列为1, 2, 6, 7, 3, 4, 5,8，如下图所示。

3 区间反转

和区间切割类似，反转 [l , r] 区间时只需将 Al-1 旋转到根，然后将 Ar +1 旋转到 Al-1 的下方，此时需要反转的 [l , r ] 区间就是 Ar+1 的左子树，对该区间的根节点打上反转懒标记即可。

八 代码

package com.platform.modules.alg.alglib.hdu3487;

public class Hdu3487 {
    public String output = "";
    private int maxn = 300010;
    private int inf = 0x3f3f3f3f;
    int n, cnt, root; // 结点数，结点存储下标累计，树根
    String op;
    boolean flag;
    private node tr[] = new node[maxn];

    void Update(int x) {
        tr[x].size = 1;
        if (tr[x].son[0] > 0)
            tr[x].size += tr[tr[x].son[0]].size;
        if (tr[x].son[1] > 0)
            tr[x].size += tr[tr[x].son[1]].size;
    }

    public Hdu3487() {
        for (int i = 0; i < tr.length; i++) {
            tr[i] = new node();
        }
    }

    // 下传翻转标记
    void Pushdown(int x) {
        if (tr[x].rev == 1) {
            tr[x].rev ^= 1;
            int temp = tr[x].son[0];
            tr[x].son[0] = tr[x].son[1];
            tr[x].son[1] = temp;
            if (tr[x].son[0] > 0)
                tr[tr[x].son[0]].rev ^= 1;
            if (tr[x].son[1] > 0)
                tr[tr[x].son[1]].rev ^= 1;
        }
    }

    // 生成新结点
    int New(int father, int val) {
        tr[++cnt].fa = father;
        tr[cnt].val = val;
        tr[cnt].size = 1;
        tr[cnt].rev = 0;
        tr[cnt].son[0] = tr[cnt].son[1] = 0;
        return cnt;
    }

    // 旋转
    void Rotate(int x) {
        Pushdown(x);
        int y = tr[x].fa, z = tr[y].fa;
        ;
        int c = (tr[y].son[0] == x) ? 1 : 0;
        tr[y].son[1 - c] = tr[x].son[c];
        tr[tr[x].son[c]].fa = y;
        tr[x].fa = z;
        if (z > 0)
            tr[z].son[tr[z].son[1] == y ? 1 : 0] = x;
        tr[x].son[c] = y;
        tr[y].fa = x;
        Update(y);
        Update(x);
    }

    // 将 x 旋转为goal的儿子
    void Splay(int x, int goal) {
        while (tr[x].fa != goal) {
            int y = tr[x].fa, z = tr[y].fa;
            if (z != goal) {
                if (((tr[z].son[0] == y ? 1 : 0) ^ (tr[y].son[0] == x ? 1 : 0)) == 0) {
                    Rotate(y);
                } else {
                    Rotate(x);
                }
            }
            Rotate(x);
        }
        // 如果 goal 是 0，则更新根为 x
        if (goal == 0) root = x;
    }

    int Findk(int x, int k) {
        while (true) {
            Pushdown(x);
            int sn = tr[x].son[0] > 0 ? tr[tr[x].son[0]].size + 1 : 1;
            if (k == sn)
                return x;
            if (k > sn) {
                k -= sn;
                x = tr[x].son[1];
            } else
                x = tr[x].son[0];
        }
    }

    int Build(int l, int r, int t, int fa) {
        if (l > r)
            return t;
        int mid = l + r >> 1;
        t = New(fa, mid);
        tr[t].son[0] = Build(l, mid - 1, tr[t].son[0], t);
        tr[t].son[1] = Build(mid + 1, r, tr[t].son[1], t);
        Update(t);
        return t;
    }

    void Init() {
        cnt = root = 0;
        tr[0].son[0] = tr[0].son[1] = 0;
        root = New(0, -inf); // 创建虚结点1
        tr[root].son[1] = New(root, inf); // 创建虚结点2
        tr[root].size = 2;
        tr[tr[root].son[1]].son[0] = Build(1, n, tr[tr[root].son[1]].son[0], tr[root].son[1]);
        Update(tr[root].son[1]);
        Update(root);
    }

    // [l,r]区间切割,插入第c个之后
    void Cut(int l, int r, int c) {
        int x = Findk(root, l - 1);
        int y = Findk(root, r + 1);
        Splay(x, 0);
        Splay(y, x);
        int tmp = tr[y].son[0];
        tr[y].son[0] = 0; // 删除
        Update(y);
        Update(x);
        x = Findk(root, c);
        y = Findk(root, c + 1);
        Splay(x, 0);
        Splay(y, x);
        tr[y].son[0] = tmp;
        tr[tmp].fa = y;
        Update(y);
        Update(x);
    }

    // [l,r]区间翻转
    void Flip(int l, int r) {
        int x = Findk(root, l - 1), y = Findk(root, r + 1);
        Splay(x, 0);
        Splay(y, x);
        tr[tr[y].son[0]].rev ^= 1; // 加翻转标记
    }

    // 中序遍历测试
    void Print(int k) {
        Pushdown(k);
        if (tr[k].son[0] > 0)
            Print(tr[k].son[0]);
        if (tr[k].val != -inf && tr[k].val != inf) {
            if (flag) {
                output += tr[k].val;
                flag = false;
            } else
                output += " " + tr[k].val;
        }
        if (tr[k].son[1] > 0)
            Print(tr[k].son[1]);
    }

    public String cal(String input) {
        int m, a, b, c;
        String[] line = input.split("\n");
        String[] num = line[0].split(" ");
        n = Integer.parseInt(num[0]);
        m = Integer.parseInt(num[1]);

        Init();
        int count = 1;
        while (m-- > 0) {
            String[] command = line[count++].split(" ");
            op = command[0];


            if (op.charAt(0) == 'C') {
                a = Integer.parseInt(command[1]);
                b = Integer.parseInt(command[2]);
                c = Integer.parseInt(command[3]);
                Cut(++a, ++b, ++c);
            } else if (op.charAt(0) == 'F') {
                a = Integer.parseInt(command[1]);
                b = Integer.parseInt(command[2]);
                Flip(++a, ++b);
            }
        }
        flag = true;
        Print(root);
        return output;
    }
}

class node {
    int son[] = new int[2];// 左右孩子0,1
    int val, fa; //值，父亲
    int size, rev; //大小，翻转标记
}

九 测试