通俗易懂的机器学习——协方差、奇异值分解、PCA降维代码实现

原理剖析

在上一篇关于降维的博客中我们已经讨论了协方差以及奇异值分解法的原理以及公式推导，在这里不在赘述，可以查看通俗易懂的机器学习——维度的诅咒（深入浅出表述机器学习降维的数学概念与实践）进行回顾。

数据选用

对于数据选用我们使用鸢尾花数据集以及瑞士卷数据集进行代码的实现以及效果的展示

为什么要使用这两个数据集呢？因为鸢尾花是机器学习入门者最常用的数据集之一，相对于多数人来讲更为熟悉，并且他的数据是四维数据，满足需要降维的条件。但是由于我们无法通过画图的方式直观的观测四维数据的分布效果，所以在此我们引入了瑞士卷数据集

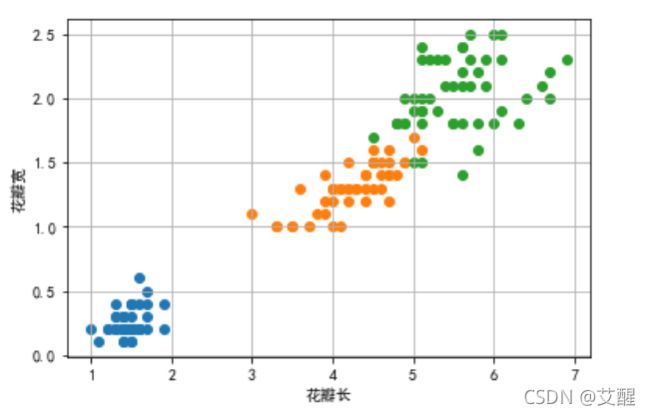
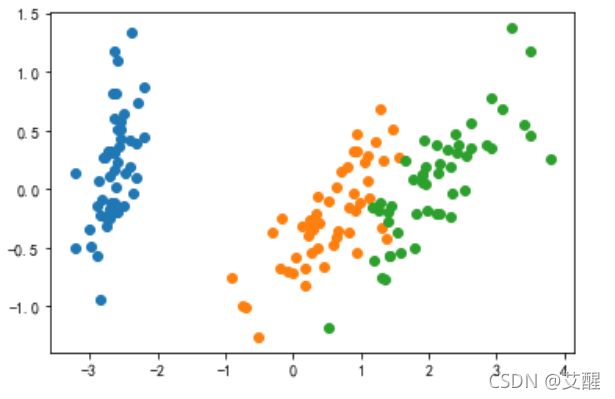
鸢尾花数据观测

既然鸢尾花数据无法通过画图的方式直观的观测数据，那为什么还有画图观察呢？首先从习惯上来讲我们首先应该观测数据集，其次我们可以选用其中一部分数据大致观测一下数据的分布情况

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from warnings import simplefilter
simplefilter(action='ignore', category=FutureWarning)

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus']=False  # 用来正常显示负号
iris = datasets.load_iris() #拿到莺尾花数据
X = iris.data[:,2:] #莺尾花的萼片长宽，花瓣长宽，这里只提取花瓣长宽数据
y = iris.target #莺尾花的类别

plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])
plt.xlabel('花瓣长')
plt.ylabel('花瓣宽')
plt.grid()

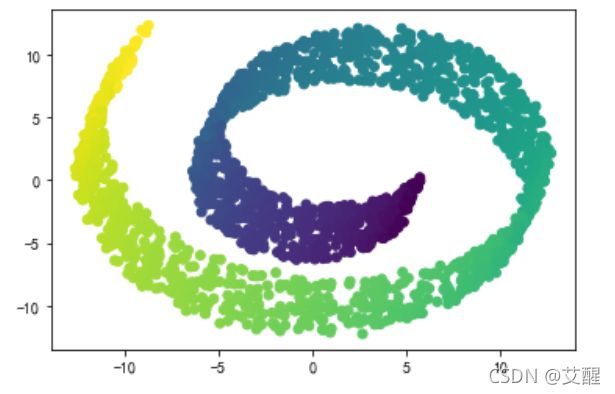
瑞士卷数据观测

from sklearn.datasets import make_swiss_roll
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

X, t = make_swiss_roll(n_samples=2000, noise=0.1)
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=t, cmap=plt.cm.Spectral,edgecolors='black')
plt.show()

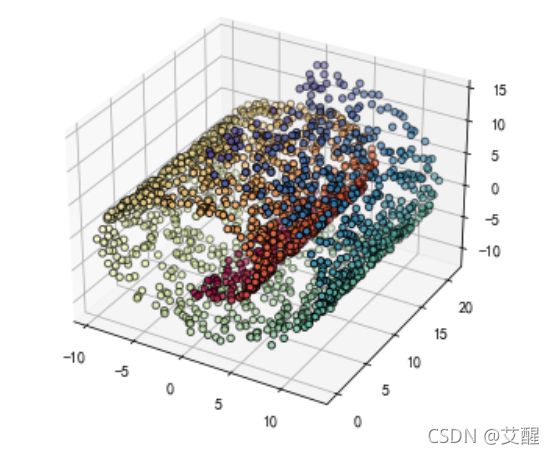
从图像中我们可以观测出对于瑞士卷的降维我们不能仅仅去掉一个坐标轴就可以完成的，而是应该在进行旋转之后再去掉一个坐标轴

代码实现

奇异值分解法

x1 = X.dot(X.T)
eig, featueVector = np.linalg.eig(x1)
x1 = x1.dot(featueVector[:,1:])
plt.scatter(x1[:,0], x1[:,1], c=t)
plt.show()

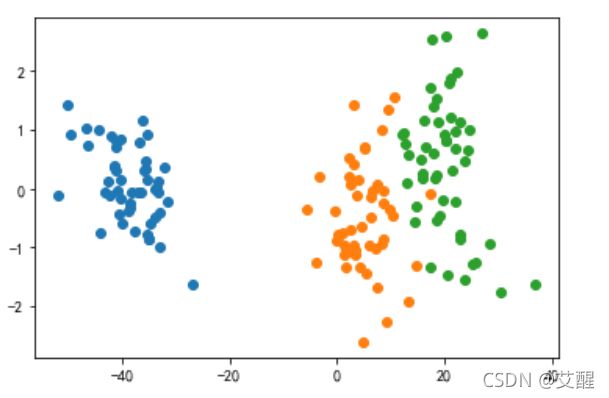
鸢尾花数据集降维后的效果

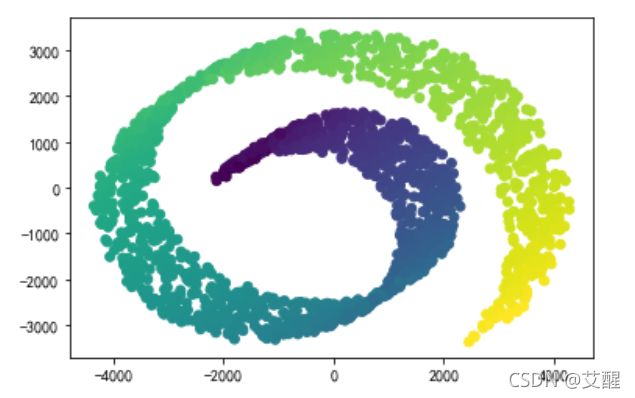
瑞士卷数据集降维后的效果

协方差法

import matplotlib.pyplot as plt
import numpy as np

X1cov=np.cov(X.T)
eig, featueVector = np.linalg.eig(X1cov)
X1new = X.dot(featueVector[:,:2])
xm = X1new.max()
plt.scatter(X1new[:,0], X1new[:,1], c=t)
plt.show()

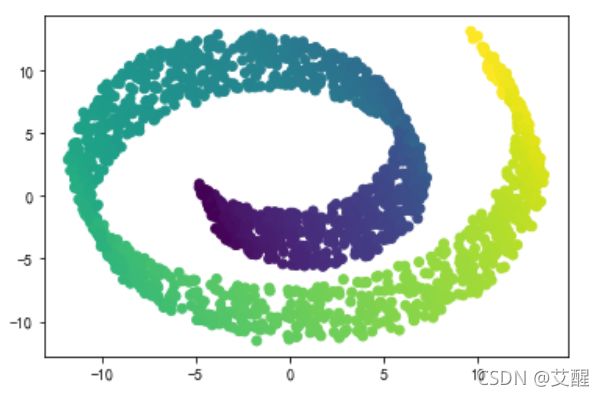
鸢尾花数据集降维后的效果

瑞士卷数据集降维后效果

sklearn中PCA方法

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
pca.fit(X)
X1new = pca.transform(X)
plt.scatter(X1new[:,0], X1new[:,1], c=t)
plt.show()

鸢尾花数据集降维后的效果

瑞士卷数据集降维后效果