机器学习笔记-神经网络的原理、数学、代码与手写数字识别
机器学习笔记-神经网络
作者:星河滚烫兮
文章目录
- 前言
- 一、神经网络的灵感
- 二、基本原理
-
- 1.神经网络最小单元——神经元
- 2.神经网络层结构
- 3.正向传播
- 4.反向传播
- 5.梯度下降
- 三、数学理论推导
-
- 1.正向传播公式推导
- 2.反向传播公式推导
-
- 1) 当前层为输出层
- 2) 当前层为隐藏层
- 3.梯度下降公式推导
- 4.公式整理
-
- 1) 正向传播
- 2) 反向传播
- 3) 梯度下降
- 四、模型建立
-
- 1.全连接层类
- 2.神经网络类
- 五、应用:手写数字识别
前言
对于特征数目较少的问题,我们大多可以通过线性回归模型、逻辑回归模型等传统机器学习算法解决,然而面对图片这一类的每一像素点为特征的复杂问题,逻辑回归已经不能够准确的解决,因为我们就算压缩图片为20*20,那么也将有400个特征,对于这400个特征的多项式组合数我们不可能人为去选择。由此有了神经网络,通过网络内部对特征复杂的组合最终得到强大的学习模型,只不过我们对其内部的运算理解不会像线性回归和逻辑回归那样简单透彻。理解了神经网络的基本原理,能够写出模型代码以解决实际问题,那么我们就真的走进了近年火热的深度学习的大门!
(本文所有代码与数据集均在Gitee上:https://gitee.com/xingheguntangxi/neural_network.git)
一、神经网络的灵感
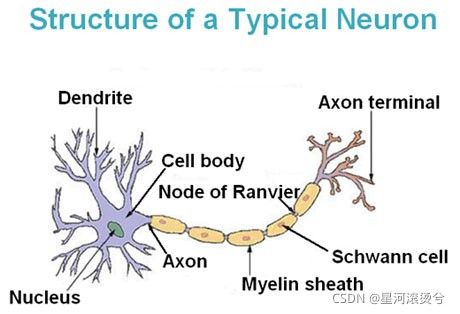
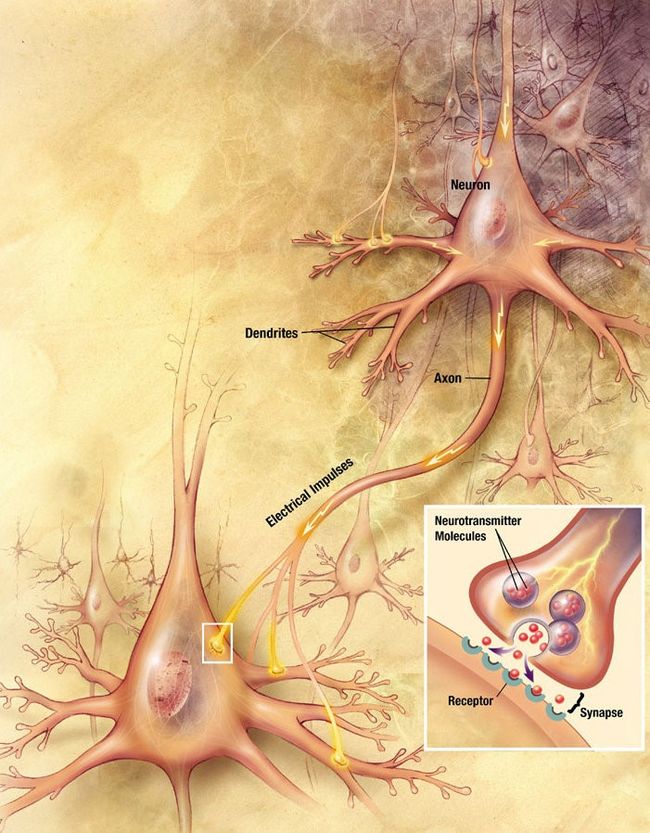
对于人类而言,包括肌肉控制、情感产生、学习思考都是由大脑完成,随着生物学的发展,科学家发现大脑又是由海量的神经元相互连接相互作用实现对身体的控制。如果将大脑看作一台电脑,那么神经元就是最小单元,它拥有接收信息、简单计算、传递信息等功能,只不过,人脑神经元是通过电信号与化学物质实现。我们想,是不是可以通过现代手段去模拟这样的人脑神经元呢?现在我们去模拟出来一个人工神经元。
首先,神经元内部要实现某种计算功能,我们不知道人脑神经元的计算是怎样的,或复杂或简单,我们姑且使人工神经元计算单一的具有某种特性的数学函数(比如sigmoid函数、Relu函数);其次,神经元要接收信息,我们给人工神经元加入输入通道;最后,神经元需要传递信息,对应的我们给人工神经元加入输出通道。至此,我们的人工神经元就可以模拟人脑神经元了,现在我们试想一下,如果我们将很多个人工神经元组合起来,说不定就能实现某种功能了呢?等等,那我们具体要怎样组合人工神经元呢?是简单的将众多神经元排成一列呢,还是画个圈圈呢,对于这个问题,我们同样是从生物本身寻找灵感。
科学家发现,大脑分为众多功能区,各区又是由某种层次结构组成。那我们的人工神经元是不是也可以像这样一层一层的排列呢,于是便有了现在的神经网络结构。为了实现不同的功能,各神经网络层的结构也不相同,本文只讲述最简单的全连接层,其它的众多结构大家日后可以深入学习。
在这里我也想谈一谈我个人的奇思异想。我们的大脑如此复杂,有上亿神经元组成不同的结构,实现不同的功能,而现在我们所拥有的大脑是经过了漫长的历史岁月进化演变而来,大脑的这些结构与功能都是经过了自然与时间的筛选。那我们的人工神经元要达到这样的程度,现有的理论还远远不够。我们的神经网络只能够处理某个单一的问题,而且神经网络的规模也与人脑相差甚远,虽然现代计算机的单一计算速度远远大于人脑。所以我有时在想,人脑神经元的计算速度比计算机低很多,生物智能的实现或许在于规模,在于进化的过程。或许可以从不同的方向研究(比如生物、医学、材料),真正的强人工智能,我们还有很长很长的一段路要走。当然,上面的也都是我个人的一些胡思乱想,当前的人工智能技术比如深度学习在各个领域都取得的辉煌的成就,所以强人工智能是遥远星空,而我们现在的AI技术让我们走的更加坚实,脚踏实地一步一步的迈向未来。
二、基本原理
1.神经网络最小单元——神经元
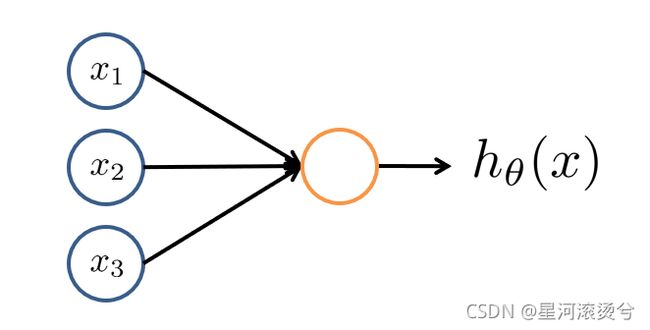
神经网络中的单个神经元,由其他神经元的输出,经过权重计算后作为当前神经元的输入,这里我们加入偏置项 x 0 = 1 x_0=1 x0=1(解释放在第三节理论推导)作为额外输入,当前神经元将输入根据权重加和得到加权输入 z = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 z=\theta_0x_0+\theta_1x_1+\theta_2x_2+\theta_3x_3 z=θ0x0+θ1x1+θ2x2+θ3x3,再将加权输入 z z z作为激活函数 g ( z ) g(z) g(z)的自变量,计算得到当前神经元的输出 y = g ( z ) y=g(z) y=g(z)。
这里的激活函数就是第一节中所说的计算单元函数,有sigmoid函数、Relu函数等。本文使用常用的sigmoid函数,原理与逻辑回归相同。
2.神经网络层结构

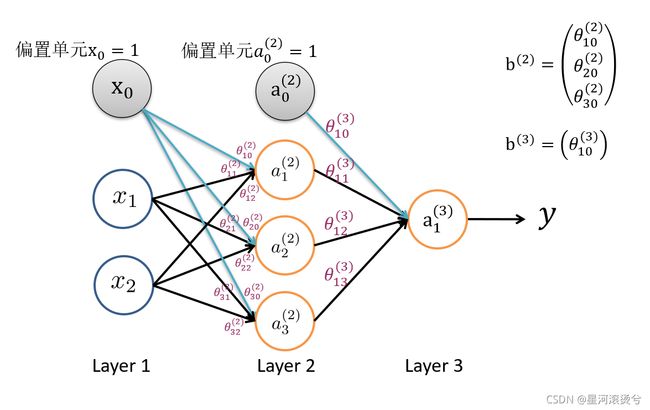
神经网络层就是神经元之间的相互作用。本文神经网络使用全连接层,顾名思义,就是相邻层的所有神经元全部连接。如上图,Layer1为输入层,Layer2为隐藏层,Layer3为输出层。对于Layer2,当前层神经元按照不同权重(重要程度)接收上一层神经元(额外添加一偏置单元 x 0 = 1 x_0=1 x0=1)的输出,将加权后的结果作为输入,当前层神经元经过激活函数计算得到输出 y = g ( z ) y=g(z) y=g(z)。如此一层一层的传递数据到输出层,得到最终神经网络模型的输出。
3.正向传播
输入层 -> 隐藏层 -> 隐藏层 -> 输出层
神经网络由输入层开始,一层一层的经过神经元激活函数的运算,最终经过最后一层即是输出层得到模型输出。正向传播会根据权重 W W W与偏置项系数 b b b更新神经网络各层的输入输出,但是参数不会发生任何变化,所以正向传播不是一个学习的过程,而是一个根据经验预测的过程。
4.反向传播
输入层 <- 隐藏层 <- 隐藏层 <- 输出层
神经网络由输出层开始,以一种长江后浪推前浪的方式,一层一层的经过梯度下降算法(或者其他高级优化算法),最终传播到输入层(不包含输入层)。反向传播会根据神经网络层的输入和输出更新该层的权重 W W W和偏置项系数 b b b,但是输入输出不会发生任何变化。反向传播就是一个学习、积累经验的过程。
5.梯度下降
大多数机器学习问题都可以用梯度下降来使函数收敛(或是局部收敛或是全局收敛),梯度下降的公式都一样, θ j = θ j − α ∂ J ( θ ) ∂ θ j \theta_j=\theta_j-\alpha\frac{\partial J(\theta)}{\partial\theta_j} θj=θj−α∂θj∂J(θ)。不熟悉的朋友可以参考线性回归和逻辑回归,本质上都一样的,只不过在神经网络中,因为具有多层多个参数矩阵,偏导项涉及到链式求导法则。
三、数学理论推导
| 变量 | 说明 |
|---|---|
| z z z | 当前层的加权输入列向量 |
| X X X | 当前层的输入列向量(包含偏置单元 x 0 x_0 x0) |
| x x x | 当前层的原始特征输入(上一层的输出) |
| a a a | 当前层的特征输出列向量(不包含偏置项) |
| y y y | 输出层的输出列向量 |
| θ \theta θ | 传递给当前层的参数矩阵(包含偏置项) |
| W W W | 传递给当前层的特征权重矩阵 |
| b b b | 传递给当前层的偏置项系数列向量 |
| l a b e l label label | 该样本对应标签 |
| l l l | 神经网络第 l l l层 |
| L L L | 神经网络共有 L L L层(输入、隐藏、输出) |
| g g g | 激活函数 |
| c o s t cost cost | 单样本输出层损失和 |
| k k k | 输出层第 k k k个神经元 |
| o u t p u t _ s i z e output\_size output_size | 输出层神经元个数 |
| δ \delta δ | 神经网络层误差项 |
| α \alpha α | 学习率 |
注:为了方便反向传播的推导计算,我们将特征输入与偏置单元分开,不将而这放入同一矩阵。
1.正向传播公式推导
我们以上图中的Layer2为例,推导向量化数学公式。对于当前层Layer2,有输入 x = ( x 1 x 2 ) x=\left(\begin{matrix}x_1\\x_2\\\end{matrix}\right) x=(x1x2),传递给当前层的特征权重矩阵 W = ( θ 11 θ 12 θ 21 θ 22 θ 31 θ 32 ) W=\left(\begin{matrix}\theta_{11}&\theta_{12}\\\theta_{21}&\theta_{22}\\\theta_{31}&\theta_{32}\\\end{matrix}\right) W=⎝⎛θ11θ21θ31θ12θ22θ32⎠⎞,偏置项系数 b = ( θ 10 θ 20 θ 30 ) b=\left(\begin{matrix}\theta_{10}\\\theta_{20}\\\theta_{30}\\\end{matrix}\right) b=⎝⎛θ10θ20θ30⎠⎞,参数矩阵 θ = ( θ 10 θ 11 θ 12 θ 20 θ 21 θ 22 θ 30 θ 31 θ 32 ) \theta=\left(\begin{matrix}\theta_{10}&\theta_{11}&\theta_{12}\\\theta_{20}&\theta_{21}&\theta_{22}\\\theta_{30}&\theta_{31}&\theta_{32}\\\end{matrix}\right) θ=⎝⎛θ10θ20θ30θ11θ21θ31θ12θ22θ32⎠⎞。
对当前层第 j j j个神经元,其加权输入为:
对当前层所有神经元,向量化处理后,其加权输入列向量为:
加权输入 z 3 × 1 z_{3\times1} z3×1经过 s i g m o i d sigmoid sigmoid函数对向量整体计算后得到当前层输出列向量:
至此,我们推导出经过正向传播获得的各层输入输出数学公式。
2.反向传播公式推导
反向传播计算梯度下降算法 θ j i = θ j i − α ∂ J ( θ ) ∂ θ j i \theta_{ji}=\theta_{ji}-\alpha\frac{\partial J\left(\theta\right)}{\partial\theta_{ji}} θji=θji−α∂θji∂J(θ)中的偏导项也就是梯度 g r a d i e n t = ∂ J ( θ ) ∂ θ j i gradient=\frac{\partial J\left(\theta\right)}{\partial\theta_{ji}} gradient=∂θji∂J(θ)。这里说明一下, θ j i \theta_{ji} θji指的是上一层第 i i i个神经元传递给当前层第 j j j个神经元的权重,可以对照上述矩阵。损失函数 J ( θ ) J(\theta) J(θ)有很多种,本文主要使用平方损失函数与交叉熵损失函数。这里我们的损失函数是单样本损失函数,而不是线性回归或逻辑回归中的计算整体平均代价,因为对整体计算量太大。损失函数如下:
对输出层的损失函数为:(k代表输出层第k个神经元)。
平方损失函数为:
交叉熵损失函数为:
因为神经网络是层层排列的,我们希望找到某种递推关系,这样反向传播计算效率会更高,所以我们在求 g r a d i e n t = ∂ c o s t ( l a b e l , y ) ∂ θ j i gradient=\frac{\partial cost(label,y)}{\partial\theta_{ji}} gradient=∂θji∂cost(label,y)时用到链式求导法则,推导需要一定的技巧。我们想要通过链式求导得到一个简单项,尽量降低复杂度。我们看正向传播推导中的 z j = θ j 0 x 0 + θ j 1 x 1 + θ j 2 x 2 z_j=\theta_{j0}x_0+\theta_{j1}x_1+\theta_{j2}x_2 zj=θj0x0+θj1x1+θj2x2,可以发现 z j z_j zj关于 θ j i \theta_{ji} θji的偏导 ∂ z j ∂ θ j i \frac{\partial z_j}{\partial\theta_{ji}} ∂θji∂zj就是 x i x_i xi,这一项是不是很简单很容易表示,所以我们对 g r a d i e n t = ∂ c o s t ( l a b e l , y ) ∂ θ j i gradient=\frac{\partial cost\left(label,y\right)}{\partial\theta_{ji}} gradient=∂θji∂cost(label,y)链式求导有:
向量化表示当前层参数 θ \theta θ梯度有:
如果将参数分为权重参数 W W W和偏置项参数 b b b有:
为了更方便的表示,我们设 δ j = ∂ c o s t ( l a b e l , y ) ∂ z j \delta_j=\frac{\partial cost\left(label,y\right)}{\partial z_j} δj=∂zj∂cost(label,y),表示当前层第 j j j个神经元的误差项。输出层与隐藏层的误差项不同,下面我们来分别推导。
1) 当前层为输出层
当当前层为输出层,有误差项 δ j ( L ) = ∂ c o s t ( l a b e l , y ) ∂ z j \delta_j^{(L)}=\frac{\partial cost\left(label,y\right)}{\partial z_j} δj(L)=∂zj∂cost(label,y),此时,求偏导使得 c o s t cost cost函数中的无关项被消除,仅剩 c o s t j ( l a b e l , y ) {cost}_j\left(label,y\right) costj(label,y), L L L代表最后一层第 L L L层。
因为 c o s t j ( l a b e l , y ) {cost}_j\left(label,y\right) costj(label,y)与输出层输出 y j y_j yj有关,而根据正向传播, y j = a j = g ( z j ) = 1 1 + e − z j y_j=a_j=g(z_j)=\frac{1}{1+e^{-z_j}} yj=aj=g(zj)=1+e−zj1, y j y_j yj又是 z j z_j zj的函数,所以有:
(9)式就是输出层通用的数学表达式,我们再利用向量整体运算将其转换为对当前层的向量表达式,其中, δ \delta δ, c o s t cost cost, y y y, g ( z ) g(z) g(z), z z z均是维度相同的列向量。:
在得到了输出层的通式之后,我们就可以根据自己选择的激活函数和损失函数,计算自己想要的输出层误差项公式。这里我们以 s i g m o i d sigmoid sigmoid激活函数加交叉熵损失函数为例,推导输出层误差项公式。
对于(10)式中的第一项有:
对于(10)式中的第二项有:
最终,将式(11)式(12)代入进式(10)即得到最终输出层误差项公式。
2) 当前层为隐藏层
当当前层为隐藏层时,有误差项 δ j ( l ) = ∂ c o s t ( l a b e l , y ) ∂ z j \delta_j^{(l)}=\frac{\partial cost\left(label,y\right)}{\partial z_j} δj(l)=∂zj∂cost(label,y),此时 c o s t cost cost为输出层所有神经元损失之和, l l l代表小于 L L L的第 l l l层隐藏层。
对于隐藏层误差项,设与所有与当前层第 j j j个神经元连接的后一层的神经元集合为 M M M, y k y_k yk与 z j z_j zj不是直接相关,而 z j z_j zj与所有后一层神经元相关,同时我们希望能够找到一种递推关系,更高效的实现反向传播,所以我们采用当前层的后一层的误差项实现递推关系,用全导数公式计算有:
对于上式第一项有:
对于上式第二项有:
代入有:
转换为当前层向量表达式为:
关于矩阵点乘的操作大家可以自己把参数矩阵和列向量画出来,更加清晰直观,也或者利用点乘条件判断。最后,我们将误差项代入上面的(6)(7)(8)式即可得到梯度表达式。
3.梯度下降公式推导
基本公式
将矩阵看作整体进行向量化运算有:
将权重与偏置项分开有:
这里我再说一下为什么要将权重与偏置项分开,而不是像之前线性回归和逻辑回归一样合并在一起。对于一般的对称结构来说,二者合并更加简洁,但是我们仔细观察神经网络的结构发现,正向传播与反向传播是不完全对称的,偏置项只做输入不做输出,偏置项不会影响反向传播的误差项,在(13)式就能看出,所以放在一起会增加一些步骤,本文的代码将权重 W W W与偏置项 b b b分开,大家也可以合并来试一试,应该会多一步对矩阵的选择(从 θ \theta θ中选择出 W W W)。
4.公式整理
| 变量 | 说明 |
|---|---|
| z z z | 当前层的加权输入列向量 |
| X X X | 当前层的输入列向量(包含偏置单元 x 0 x_0 x0) |
| x x x | 当前层的原始特征输入(上一层的输出) |
| a a a | 当前层的特征输出列向量(不包含偏置项) |
| y y y | 输出层的输出列向量 |
| θ \theta θ | 传递给当前层的参数矩阵(包含偏置项) |
| W W W | 传递给当前层的特征权重矩阵 |
| b b b | 传递给当前层的偏置项系数列向量 |
| l a b e l label label | 该样本对应标签 |
| l l l | 神经网络第 l l l层 |
| L L L | 神经网络共有 L L L层(输入、隐藏、输出) |
| g g g | 激活函数 |
| c o s t cost cost | 单样本输出层损失和 |
| k k k | 输出层第 k k k个神经元 |
| o u t p u t _ s i z e output\_size output_size | 输出层神经元个数 |
| δ \delta δ | 神经网络层误差项 |
| α \alpha α | 学习率 |
1) 正向传播
z 3 × 1 = W ⋅ x + b ( 1 ) z_{3\times1}=W\cdot x+b\ \ \ \ \ (1) z3×1=W⋅x+b (1)
a 3 × 1 = g ( z ) = 1 1 + e − z ( 2 ) a_{3\times1}=g(z)=\frac{1}{1+e^{-z}}\ \ \ \ \ (2) a3×1=g(z)=1+e−z1 (2)
2) 反向传播
c o s t ( l a b e l , y ) = ∑ k = 1 o u t p u t _ s i z e [ − l a b e l k ln y k − ( 1 − l a b e l k ) ln ( 1 − y k ) ] ( 4 ) cost(label,y)=\sum_{k=1}^{output\_size}[-{label_k}\ln{y_k}-(1-{label_k})\ln{(1-y_k)}]\ \ \ \ \ (4) cost(label,y)=k=1∑output_size[−labelklnyk−(1−labelk)ln(1−yk)] (4)
∂ c o s t ( l a b e l , y ) ∂ W ( l ) = ∂ c o s t ( l a b e l , y ) ∂ z ( l ) ⋅ x ( l ) T = δ ( l ) ⋅ x ( l ) T ( 7 ) \frac{\partial cost\left(label,y\right)}{\partial W^{(l)}}=\frac{\partial cost\left(label,y\right)}{\partial z^{(l)}}{\cdot}x^{{(l)}^T}=\delta^{(l)}{\cdot} x^{{(l)}^T}\ \ \ \ \ (7) ∂W(l)∂cost(label,y)=∂z(l)∂cost(label,y)⋅x(l)T=δ(l)⋅x(l)T (7)
∂ c o s t ( l a b e l , y ) ∂ b ( l ) = ∂ c o s t ( l a b e l , y ) ∂ z ( l ) = δ ( l ) ( 8 ) \frac{\partial cost\left(label,y\right)}{\partial b^{(l)}}=\frac{\partial cost\left(label,y\right)}{\partial z^{(l)}}=\delta^{(l)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8) ∂b(l)∂cost(label,y)=∂z(l)∂cost(label,y)=δ(l) (8)
输出层误差项:
δ ( L ) = ∂ c o s t ( l a b e l , y ) ∂ y × ∂ g ( z ( L ) ) ∂ z ( L ) ( 10 ) \delta^{(L)}=\frac{\partial cost\left(label,y\right)}{\partial y}\times\frac{\partial g(z^{(L)})}{\partial z^{(L)}}\ \ \ \ \ (10) δ(L)=∂y∂cost(label,y)×∂z(L)∂g(z(L)) (10)
∂ c o s t ( l a b e l , y ) ∂ y = − l a b e l y + 1 − l a b e l 1 − y o r ∂ c o s t ( l a b e l , y ) ∂ y = − ( l a b e l − y ) ( 11 ) \frac{\partial cost\left(label,y\right)}{\partial y}=-\frac{label}{y}+\frac{1-label}{1-y}\ \ or\ \ \frac{\partial cost\left(label,y\right)}{\partial y}=-(label-y)\ \ \ \ \ (11) ∂y∂cost(label,y)=−ylabel+1−y1−label or ∂y∂cost(label,y)=−(label−y) (11)
∂ g ( z ( L ) ) ∂ z ( L ) = [ 1 − g ( z ( L ) ) ] × g ( z ( L ) ) = ( 1 − y ) × y ( 12 ) \frac{\partial g(z^{(L)})}{\partial z^{(L)}}=[1-g(z^{(L)})]×g(z^{(L)})=(1-y)×y \ \ \ \ \ (12) ∂z(L)∂g(z(L))=[1−g(z(L))]×g(z(L))=(1−y)×y (12)
隐藏层误差项:
δ ( l ) = [ 1 − g ( z ( l ) ) ] g ( z ( l ) ) × W ( l + 1 ) T ⋅ δ ( l + 1 ) = ∂ g ( z ) ∂ z × W ( l + 1 ) T ⋅ δ ( l + 1 ) ( 13 ) \delta^{(l)}=[1-g(z^{(l)})]g(z^{(l)})\times W^{{(l+1)}^T}\cdot\delta^{(l+1)}=\frac{\partial g(z)}{\partial z}\times W^{{(l+1)}^T}\cdot\delta^{(l+1)}\ \ \ \ \ (13) δ(l)=[1−g(z(l))]g(z(l))×W(l+1)T⋅δ(l+1)=∂z∂g(z)×W(l+1)T⋅δ(l+1) (13)
3) 梯度下降
W ( l ) = W ( l ) − α δ ( l ) ⋅ x ( l ) T ( 15 ) W^{(l)}=W^{(l)}-\alpha\delta^{\left(l\right)}\cdot x^{\left(l\right)^T}\ \ \ \ \ (15) W(l)=W(l)−αδ(l)⋅x(l)T (15)
b ( l ) = b ( l ) − α δ ( l ) ( 16 ) b^{(l)}=b^{(l)}-\alpha\delta^{\left(l\right)}\ \ \ \ \ (16) b(l)=b(l)−αδ(l) (16)
在以上公式中, ∂ c o s t ( l a b e l , y ) ∂ y \frac{\partial cost\left(label,y\right)}{\partial y} ∂y∂cost(label,y)和 ∂ g ( z ( L ) ) ∂ z ( L ) \frac{\partial g(z^{(L)})}{\partial z^{(L)}} ∂z(L)∂g(z(L))根据损失函数和激活函数的选择而定。
四、模型建立
1.全连接层类
我们这里最小结构为单个样本的神经网络层,所以我们首先要定义全连接层实现类,选择激活函数与损失函数,在类中实现单样本当前层的正向传播、反向传播、梯度下降等基本操作。代码中有一个地方需要注意,反向传播的误差项分输出层和隐藏层,输出层的误差项我们单独计算,而隐藏层的误差项就根据后一层的误差项递推计算。所以我们的 F u l l C o n n e c t e d L a y e r . d e l t a FullConnectedLayer.delta FullConnectedLayer.delta计算的是当前层的上一层的误差项。代码如下:
激活函数与损失函数:
# 神经元激活函数选择
class sigmoid:
"""
sigmoid激活函数
"""
def forward(self, z):
"""
正向传播表达式
z:加权输入θ@X
"""
return 1.0 / (1.0 + np.exp(-z))
def backward(self, output):
"""
output:就是当前层的输出g(z)即是y
:return:返回该激活函数的偏导数dg(z)/dz
"""
return output * (1.0-output)
"""
损失函数选择
对于不同损失函数,仅仅代价函数J关于输出层加权输入z的偏导数dJ/dZ不同(输出层误差项不同),
而隐藏层的误差项均是由前一误差项递推而来,公式相同。
"""
class Square_J:
# 平方损失函数
def cost(self, label, output):
# 单项损失函数
return 0.5 * np.sum((label-output)**2)
def d_outlayer(self, label, output):
"""
求代价函数J关于输出层的输出[y=g(z)]的偏导数
:return: 偏导数值
"""
return -(label - output)
class CrossEntropy_J:
# 交叉熵损失函数(为避免0带给log与分数到来的数值问题,我们加入0的近似值1e-5)
def cost(self, label, output):
# 单项损失函数
return np.sum(-label*np.log(output+1e-5) - (1-label)*np.log(1-output+1e-5))
def d_outlayer(self, label, output):
"""
求代价函数J关于输出层的输出[y=g(z)]的偏导数
:return: 偏导数值
"""
return (-label/(output+1e-5)) + ((1-label)/(1-output+1e-5))
神经网络全连接层类:
class FullConnectedLayer:
"""
全连接层实现类:实例对象为神经网络的某一层,对该层进行正向传播、反向传播(计算误差项)、梯度下降等操作
"""
def __init__(self, input_size, output_size, activator):
"""
input_size: 当前层神经元输入列向量的维度(即上一层神经元个数)
output_size: 当前层神经元的输出列向量的维度(即当前层神经元个数)
activator: 选择不同激活函数
"""
self.input_size = input_size
self.output_size = output_size
self.activator = activator
self.W = np.random.uniform(-0.1, 0.1, (output_size, input_size)) # 初始化传递给当前层的权重参数
self.b = np.zeros((self.output_size, 1)) # 初始化传递给当前层的偏置项(当前层神经元个数的列向量)
self.input = [] # 当前层输入(上一层神经元输出)
self.output = [] # 当前层输出
self.delta = [] # 上一层层神经元的误差项δ(注意这里是上一层的误差项δ)
self.gradient_W = [] # 传递给当前层的权重梯度矩阵(即dJ/dW)
self.gradient_b = [] # 传递给当前层的偏置项梯度列向量(即dJ/db)
def forward(self, input):
"""
正向传播函数:更新属性:当前层的输入输出
input: 当前层神经元的输入(上一层神经元的输出)
"""
z = np.dot(self.W, input) + self.b # 计算加权输入:z=W@X+b <=> z=θ@X
self.input = input
self.output = self.activator.forward(z)
def backward(self, delta):
"""
反向传播函数:计算上一层的误差项(因为我们计算隐藏层误差项是通过递推,而输出层误差项我们在模型里单独计算)
delta: 后一层神经元的误差项向量
"""
self.delta = self.activator.backward(self.input) * (self.W.T @ delta) # 递推公式计算上一层的误差项δ
self.gradient_W = delta @ self.input.T # 更新传递给当前层权重梯度矩阵
self.gradient_b = delta # 更新传递给当前层偏置项梯度矩阵
def gradient_descent(self, rate):
"""
梯度下降函数:实现简单的梯度下降算法(高级优化算法有兴趣可以自行实现)
rate:学习率
"""
self.W = self.W - rate*self.gradient_W # 更新传递给当前层的权重矩阵
self.b -= rate * self.gradient_b # 更新传递给当前层的偏置项矩阵
2.神经网络类
然后,我们定义神经网络模型类,我们在这个类里面调用全连接层类,实现单样本所有层的正向传播、反向传播、梯度下降操作,并以此训练模型、预测、计算损失值、根据测试集计算准确率。除此之外,为了避免我们写的代码存在不易察觉的bug,我们内置梯度检查函数,梯度检查的基本原理就是根据 J − θ J-\theta J−θ函数各点的近似斜率与数学推导计算出的斜率(梯度)作比较,如果二者相差极小则认为模型计算梯度正确,否则就应该检查代码是否有bug。代码如下:
class Neural_Network:
"""
神经网络模型:实现训练、预测、计算损失、梯度检查等功能
"""
def __init__(self, layers_struct, J):
"""
layers_struct:神经网络层结构,每层神经元个数保存在数组中,例如[3, 5, 5, 4]
J:选择代价函数:1.平方损失函数;2.交叉熵损失函数
"""
self.rate = 0.033 # 学习率
self.EPOCH = 30 # 训练轮数
self.layers = [] # 保存该模型各全连接层对象
self.J = J # 模型选择的损失函数
# 根据输入的神经网络结构初始化各全连接层
for i in range(len(layers_struct)-1):
self.layers.append(FullConnectedLayer(layers_struct[i], layers_struct[i+1], sigmoid()))
def predict(self, sample):
"""
预测指定单个样本
sample: 单个样本
:return: 预测结果(layer.output)
"""
output = sample
# 进行正向传播
for layer in self.layers:
layer.forward(output)
output = layer.output
return output
def cal_gradient(self, label):
"""
计算模型各层梯度
label:当前样本的标签
"""
# 单独计算输出层误差项δ,然后从后到前递推计算隐藏层误差项δ
delta = (self.layers[-1].activator.backward(self.layers[-1].output) * self.J.d_outlayer(label, self.layers[-1].output))
for layer in self.layers[::-1]:
layer.backward(delta)
delta = layer.delta
def update_weight(self):
# 更新模型各层系数矩阵(W、b)
for layer in self.layers:
layer.gradient_descent(self.rate)
def cost(self, label, output):
# 计算单个样本的损失值
return self.J.cost(label, output)
def train_one_sample(self, sample, label):
"""
训练单个样本
sample:单样本属性
label:单样本标签
"""
self.predict(sample) # 正向传播更新各层输入输出
self.cal_gradient(label) # 反向传播更新各层参数的梯度
self.update_weight() # 梯度下降更新各层参数
def train(self, dataset, labels):
"""
训练模型
dataset:数据集特征(应当是三维数组,单个样本的特征用列向量表示)
labels: 数据集标签(应当是三维数组,单个样本的标签用列向量0/1表示类别,序号与数据集特征一一对应)
"""
for i in range(self.EPOCH):
cost = 0
print(f"正在进行第{i+1}轮训练:")
for j in range(len(dataset)):
self.train_one_sample(dataset[j], labels[j])
cost += self.cost(labels[j], self.predict(dataset[j]))
print(f"第{i+1}轮训练已完成,损失值J={cost/len(dataset)}") # 计算模型损失值
def check_gradient(self, sample, label):
"""
梯度检查函数J-W,注意检查完毕后要关闭该函数。梯度检查独立于模型训练之外,可以单独运行
sample:单个数据
label:数据标签
print:输出期望梯度与实际梯度的差值,观察梯度检查是否正确
"""
# 首先正向传播一遍获得各层输入输出,再反向传播计算各层梯度
self.predict(sample)
self.cal_gradient(label)
epsilon = 10e-4 # 设置极小项ε
# 逐一计算每一层每一个参数的梯度是否正确
for layer in self.layers:
for i in range(layer.W.shape[0]):
for j in range(layer.W.shape[1]):
layer.W[i, j] += epsilon
output = self.predict(sample) # 更新当前层的输出
J2 = self.cost(label, output) # 根据设置的w系数计算代价函数J(w+ε)
layer.W[i, j] -= 2 * epsilon
output = self.predict(sample) # 更新当前层的输出
J1 = self.cost(label, output) # 根据设置的w系数计算代价函数J(w-ε)
except_gradient = (J2-J1) / (2*epsilon) # 计算期望梯度
print(f"对W进行梯度检查有:except_gradient - actual_gradient = {except_gradient-layer.gradient_W[i, j]}")
def accuracy(self, test_X, test_y):
"""
计算测试集准确率
:param test_X: 测试数据集特征
:param test_y: 测试数据集标签
:return : 返回模型准确率
"""
n = 0
for i in range(len(test_X)):
predict = self.predict(test_X[i])
#print(f"第{i+1}组预测:\n{test_y[i]}\n --> \n{predict}")
if predict.argmax() == test_y[i].argmax():
n += 1
return n / len(test_X)
def save_model(self, filename):
"""
保存模型参数至txt文件中
:param filename: 文件路径
"""
with open(filename, 'a') as f:
f.truncate(0) # 每次重新保存模型时,删除历史数据
for layer in self.layers:
np.savetxt(f, np.c_[layer.W], fmt='%.6e', delimiter='\t') # 保存权重矩阵用6位科学计数法表示,用\t分隔
np.savetxt(f, np.c_[layer.b], fmt='%.6e', delimiter='\t') # 保存偏置项列向量用6位科学计数法表示,用\t分隔
def load_model(self, filename):
"""
从txt文件中读取加载模型参数
:param filename: 文件路径
"""
with open(filename, 'r') as f:
lines = f.readlines() # 将txt文件中的所有数据按行以字符串形式存入lines数组
for i in range(len(lines)):
lines[i] = lines[i].split('\t') # 按\t分隔参数
lines[i][-1] = lines[i][-1].replace('\n', '') # 去掉每行最后一个元素的换行符\n
for j in range(len(lines[i])):
lines[i][j] = np.float(lines[i][j]) # 将所有字符串类型的元素转换为与模型参数相同类型的np.float
last = 0
for layer in self.layers: # 加载各层神经元参数
layer.W = np.array(lines[last:last+layer.output_size]).reshape((layer.output_size, layer.input_size))
layer.b = np.array(lines[last+layer.output_size:last+layer.output_size*2]).reshape((layer.output_size, 1))
last = last + layer.output_size*2
最后,因为训练模型的时间很长,我们不想每次都重新训练,所以我们在神经网络模型中内置save_model与load_model函数,将训练好的模型参数保存在txt文档中,下次可以直接加载模型。
五、应用:手写数字识别
我使用了两个数据集,第一个是吴恩达老师的.mat数据集,大小为5000张20*20的手写数字图片,已进行列向量展开与归一化。第二个是MNIST数据集,大小为60000张28*28的手写数字图片,未进行处理。数据集读取方法我放在了/dataset/readme.txt文档中,最终模型准确率能达到约98.5%。
以下是数据预处理代码:
def load_data(path):
# 加载.mat数据集
data = sio.loadmat(path)
y = data.get('y') # (5000,1)
y = y.reshape(y.shape[0]) # make it back to column vector
X = data.get('X') # (5000,400)
return X, y
def data_process(X, y, normal=True):
"""
数据预处理:列向量展开,归一化,随机排列,标签向量化
:param X: 三维特征数据集
:param y: 一维标签数据集
:param normal: 是否进行归一化
:return: 三维特征数据集, 三维标签数据集
"""
# 列向量展开
X = X.reshape((X.shape[0], X.shape[1] * X.shape[2]))
# 归一化处理
if normal:
X = (X - np.min(X)) / (np.max(X) - np.min(X))
# 随机排列
whole = np.insert(X, 0, y, axis=1)
np.random.shuffle(whole)
y = whole[:, 0]
X = np.delete(whole, 0, axis=1)
# 标签向量化
y_matrix = []
for i in range(0, 10):
y_matrix.append((y == i).astype(int))
y_matrix = np.array(y_matrix).T
# 分割为列向量
new_X = np.array(X).reshape((len(X), len(X[0]), 1))
new_y = np.array(y_matrix).reshape((len(y_matrix), len(y_matrix[0]), 1))
return new_X, new_y
关于本项目的全部代码和数据集,我会放在Gitee上,https://gitee.com/xingheguntangxi/neural_network.git,大家自行下载。另外,我自己也写了十张手写数字0-9,都能识别出来,不过9这个数字似乎正确率不高,大家感兴趣可以自己试试呀^_^
吴恩达机器学习 https://study.163.com/course/courseMain.htm?courseId=1210076550
零基础入门深度学习(3) - 神经网络和反向传播算法https://www.zybuluo.com/hanbingtao/note/476663