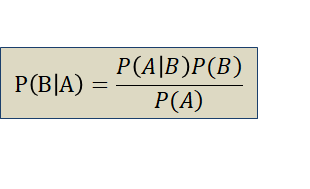05.数据的深度分析（数据挖掘、机器学习）--《数据科学概论》

前言：基于人大的《数据科学概论》第五章，数据的深度分析（数据挖掘、机器学习）。主要是机器学习与数据挖掘、具体的算法、主流工具、特征选择的内容。

一、机器学习与数据挖掘

**简说：**从基础数据计算一些聚集统计量（Aggregations），生成报表（Reports），观察同比/环比的变化，以及通过数据透视表（Pivotal Table），从不同维度观察数据的汇总信息，只能算是对数据的简单分析。

• 要从数据里挖掘和提取隐含的模式和规律，简单分析是无能为力的。我们需要在数据上运行更加复杂的算法。这些算法主要是机器学习和数据挖掘算法。

（1）什么是机器学习？

• 从广义上来说，机器学习是一种能够赋予机器学习的能力，让他完成直接编程无法完成的功能的方法。
• 但从实践上来说，机器学习是一种通过利用数据，训练处模型，然后使用模型预测的一种方法。
• 由此可见，数据对于机器学习的意义，可以说数据是原材料，机器学习是加工工具，模型是产品。我们可以利用这个产品做预测，指导未来的决策。

1、机器学习和人工智能紧密关联

• 人工智能研究的联接主义（如神经网络）和符号主义（如符号推理系统）

（2）什么是数据挖掘？

数据挖掘，可以认为是机器学习算法在数据库上的应用，很多数据挖掘中的算法是机器学习算法在数据库中的优化。

但是，数据挖掘能够形成自己的学术圈，是因为它也贡献了独特的算法，其中最著名的是关联规则分析方法Apriori

（3）机器学习的目的

机器学习的目的是分类和预测。所谓的分类是根据输入数据，判断这些数据隶属于哪个类别（Category）。而预测则是根据输入数据，计算一个输出值（Numeric）。输入数据一般为一个向量，也称为特征（Feature），输出则是一个分类或者一个数值。

（4）机器学习的基本过程

机器学习的基本过程是用训练数据（包含输入数据和预期输出的分类或者数值）训练一个模型（Model），利用这个模型，就可以对新的实例数据（Instances）进行分类和计算一个预测值。

（5）监督、非监督、半监督学习

• 监督学习是机器学习的一种类别，训练数据由输入特征（features）和预期的输出构成，输出可以是一个连续的值（称为回归分析），或者是一个分类的类别标签（称为分类）。
• 无监督学习与监督学习的区别是，它没有训练样本，直接对数据进行建模。
• 半监督学习，是监督学习与无监督学习相结合的一种学习方法。它研究如何利用少量的标注样本和大量的未标注样本进行训练和预测的问题。半监督学习包括半监督分类、半监督回归、半监督聚类和半监督降维算法。

二、具体的机器学习算法

2.1决策树

定义：在机器学习中，决策树是一个预测模型，它表示对象属性（比如贷款用户的年龄、是否有工作、是否有房产、信用评分等）和对象值（是否批准其贷款申请）之间的一种映射。决策树中的非叶子节点，表示用户对象属性的判断条件，其分支表示符合节点条件的所有对象，树的叶子节点表示对象所属的预测结果。

（1）决策树构造过程

• 决策树的创建从根节点开始，也就是需要确定一个属性，根据不同记录在该属性上的取值，对所有记录进行划分。接下来，对每个分支重复这个过程，即对每个分支，选择一个另外一个未参与树的创建的属性，继续对样本进行划分，一直到某个分支上的样本都属于同一类（或者隶属该路径的样本大部分属于同一类）
• 属性的选择也称为特征选择，特征选择的目标，是使得分类后的数据集比较纯。
• 其中一个应用广泛的度量函数，是信息增益（Information Gain）
  

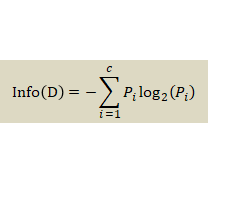
（2）决策树的裁剪

在决策树建立的过程中，很容易出现过拟合的现象（Overfitting）

• 过拟合是指模型非常逼近训练样本，模型是在训练样本上训练出来的，在训练样本上预测的准确率很高，但是对测试样本的预测准确率不高，效果并不好（有不必要的属性）。
• 剪枝分为预先剪枝和后剪枝两种情况。
  • 预先剪枝指的是在决策树构造过程中，使用一定条件加以限制，在产生完全拟合的决策树之前就停止生长。
  • 后剪枝是在决策树构造完成之后，也就是所有的训练样本都可以用决策树划分到不同子类以后，按照自底向上的方向，修建决策树。
• 使得模型不要过于复杂。

2.2聚类分析K-means算法

K-means算法是最简单的一种聚类算法，属于无监督学习算法。

• 假设我们的样本是{x^(1)，x(2)，…，x^(m)},每个x(i) 属于R^n。现在用户给定一个K值，要求将样本聚类（CLustering）成K个类簇（Cluster）。
  

K-means算法的缺点

1. K-means算法中K是事先给定的，一个适合的K值难以估计。
2. 在K-means算法中，首先需要根据初始类簇中心来确定一个初始划分，然后对初始划分进行优化。这个初始类簇中心的选择，对聚类结果有较大的影响，一旦初始值选择的不好，可能无法得到有效的聚类效果。可以使用遗传算法（Genetic Algorithm），帮助选择合适的初始类簇中心。
3. 算法需要不断进行样本分类调整，不断地计算调整后的新的聚类中心，因此当数据量非常大时，算法的时间开销是非常大的。

2.3分类算法支持向量机SVM

• 支持向量机由Boser、Guyon、Vapnik等，在1992年的ACM Conference on Computational Learning Theory（COLT）会议上提出。从那以后，支持向量机以其在解决小样本、非线性、以及高维模式识别中，表现出来的特有优势，获得广泛的应用。其应用领域包括文本分类、图像识别等。

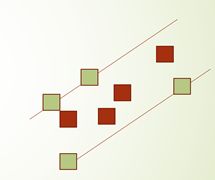
1、二维空间（即平面）数据点的分类

通过一个二维平面上的简单分类，来介绍支持向量机分类技术。

2、支持向量

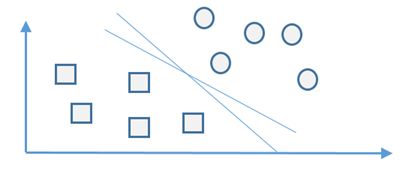
• 我们寻找分类函数 y = f(x) = w^t x+b,超平面上的点代入这个分类函数，得到f(x) =0;超平面一边的数据点代入分类函数，得到f(x) =1 ；超平面另外一边的数据点代入分类函数，得到f(x) = -1.在二维平面上，这个分类函数对应一根直线y=f(x) = ax+b
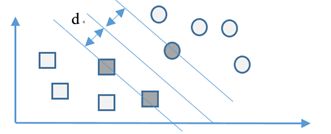
• 如何确定W和b呢？答案是寻找一个超平面，它到两个类别数据点的距离都尽可能大。这样的超平面为最优的超平面。

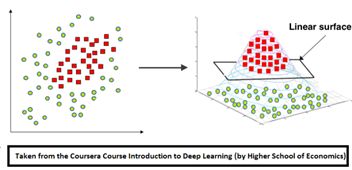
3、核函数技巧

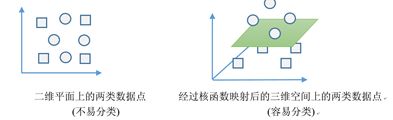
• 有时候两个数据点集，在低维空间中，我们无法找到一个超平面来进行清清晰的划分，如图中额的二维平面上的两类数据点，找不到一根直线把他们划分开。SVM数据分析方法里，有一个核函数（Kernel Function）技巧，可以巧妙地解决这个问题。通过核函数，可以把低维空间的数据点（向量）映射到高维空间的数据点，经过映射以后，两类数据点在高维空间里，可以有一个超平面把他们分开。

4、异常值的处理

• 超平面本身是由少数几个支持向量（Support Vector）确定的，未考虑Outline（离群值，异常值）的影响。
• 这个问题，通过在模型中引入**松弛变量**（Relax Variable）来解决，松弛变量是为了纠正或约束少量“不安分”或脱离集体不好归类的数据点的因子。
• 支持向量机不仅能够处理线性分类，能够处理数据中的非线性（使用核函数）、容忍异常值（使用松弛变量），是一个强大的分类器。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NLKuHZtD-1609316416847)(image-20201226120241362.png)]

5、支持向量回归及其特点

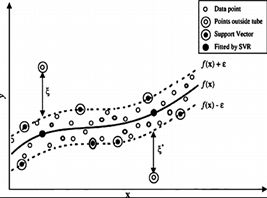
支持向量回归的特点

• 可以把非线性函数f(x),看作是多维空间的一条曲线，训练数据点分布在这个曲线周围，形成一个“管道”。所有训练数据点，只有分布在“管道”壁上的那些训练数据点，才决定管道的位置。于是这些训练数据点，就称为“支持向量”。
• 具体到二维平面空间，SVM的目的是通过一条直线，尽量把两类数据点分开。而**SVR则通过一个管道，尽量把数据点都囊括进来。**

2.4关联规则分析

简说：关联规则分析，最典型的例子是购物篮分析。通过关联规则分析，能够发现顾客每次购物交易的购物篮中的不同商品之间的关联，从而了解客户的消费习惯，让商家能够了解哪些商品被客户同时购买，从而帮助他们制定更好的营销方案。

• 关联规则是形如X->Y的蕴含式，表示通过X可以’推导出“ Y，X称为关联规则的左部（Hand Side ，LHS），Y称为关联规则的右部（Right Hand Side，RHS）。在购物篮分析结果里，“尿布->啤酒”表示客户在购买尿布的同时，有很大的可能性购买啤酒。
• 关联规则有两个指标，分别是支持度（Support）和置信度（Confidence）。
• 关联规则A->B的支持度support = P（AB），指的是事件A和事件B同时发生的概率。
• 置信度confidence = P（B|A）= P（AB）/P（A），指的是是发生事件A的基础上，发生事件B的概率。
  • 比如，如果“尿布->啤酒”，关联规则的支持度为30%，置信度为60%，那么就表示所有的商品交易中，30%交易同时购买了尿布和啤酒，而在购买尿布的交易中，60%的交易同时购买了啤酒。

（1）Apriori算法

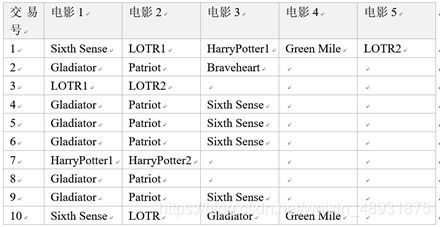
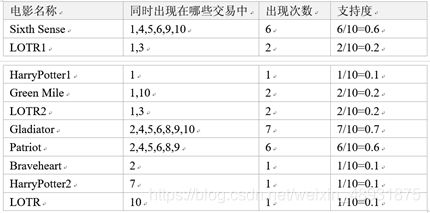
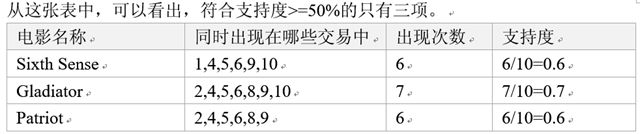
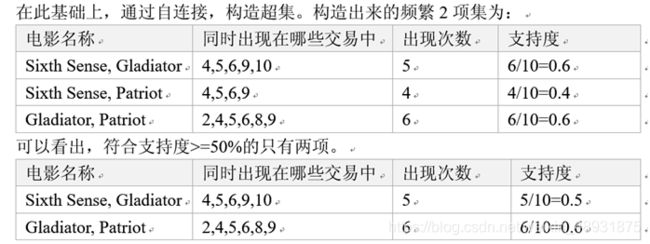
挖掘关联规则的主流算法为Apriori 算法。他的基本原理是，在数据集中找出同时出现概率符合预定义（Pre-defined）支持度的频繁项集，而后从以上频繁项集中，找出符合预定义置信度的关联规则。

• 下面的实例中，我们的目标是，从这些数据中，挖掘出用户观看电影的关联规则，即购票观看某部（几部）电影的用户中，有多少比例会去购票观看其它哪些电影。
  

频繁1项集为：

频繁2项集为：

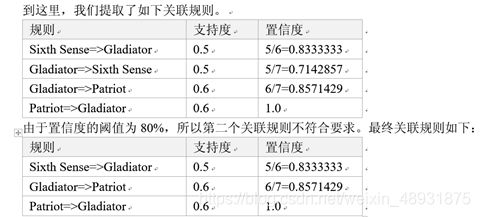
1. 购票观看“sixth sense "的用户中，有83%会购票观看 ”Gladiator“，而同时购票观看这两部电影的用户占50%。
2. 购票观看“Gladiator”的用户中，有85.7%会观看“Patriot”，而同时购票观看这两部电影的用户占60%。
3. 购票观看“patriot”的用户中，100%同时也会购票观看“Gladiator”，而同时购票观看这两部电影的用户占60%。

2.5、EM算法（Expectation-Maximization）算法

EM（最大期望）算法，是在概率模型（Probability Distribution Model）中，寻找参数的最大似然估计的算法。其中，这个概率模型包括无法观测的隐藏变量（Latent Variable）。EM算法一般用于机器学习的聚类。

（1）一个栗子

假设我们用硬币A和硬币B进行投掷硬币实验。这两个硬币在进行投掷实验时，正面朝上的概率分别为θA和θB。我们进行了5轮投掷实验，每轮实验要么选择硬币A，要么选择硬币B，一共连续投掷10次，每次投掷结果要么正面朝上(用H表示)，要么背面朝上(用T表示)。于是我们得到5个正面/背面标志列表

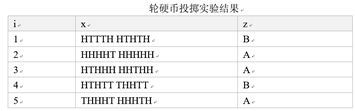
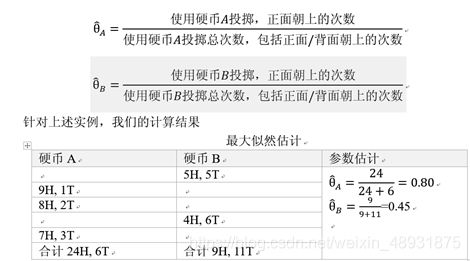
（2）EM算法实例

• 现在我们考虑参数估计的另外一种情形。也就是，我们仅仅获得了向量列表x=(x1, x2, …, x5)，但是没有对应的z=(z1, z2, … z5)。也就是我们知道每轮投掷的10次投掷的正面/背面情况，但是不知道每轮是用硬币A还是硬币B。
• 我们把z称为隐藏变量(Hidden Variables)或者潜在因子(Latent Factors)。在这种情况下，参数估计是在数据不全(Incomplete Data)的情况下进行的。
  
  

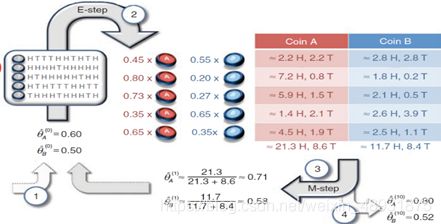
2.6、协同过滤推荐算法（Collaborative Filtering Recommendation）

简说：信息的极度爆炸，使得人们找到他们需要的信息变得越来越难。面对海量的数据，用户需要更加智能的、更加了解他们的需求、口味、和喜爱的信息发现机制，于是推荐系统孕育而生。

对推荐系统进行分类：

1. 根据推荐系统是否为不同用户推荐不同的物品或者内容，推荐系统分为个性化推荐和大众化推荐系统。
2. 根据推荐系统使用的数据源，推荐系统分为基于内容的推荐系统、基于人口统计学的推荐系统、基于协同过滤的推荐。
3. 根据推荐模型的基本技术原理，推荐系统分为基于用户和物品评价矩阵的推荐系统、基于关联规则的推荐系统、基于模型的推荐。

（1）基于内容的推荐

基于内容的推荐的基本思路是，根据物品或者内容的描述信息，发现他们之间的相似性，然后基于用户以往的偏好历史记录，推荐相似的物品或者内容。

简单来说就是，用户喜欢什么就给他推荐什么。

• 例子：比如在电影推荐里，我们首先需要对电影的描述信息（元数据）进行建模，这个模型可以包括电影的类型、电影的导演、电影的演员等。对于具体用户，根据他历史上喜欢看的电影，可以给他推荐类似的电影。这里就需要上述的描述信息，计算电影之间的相似度。
• 问题：
  • 推荐的质量依赖于对物品模型的完整和全面程度。
  • 物品相似度的分析没有考虑人对物品的态度。
  • 需要基于用户以往的喜好历史做出推荐，于是存在冷启动问题。
    • 冷启动问题是模型刚开始运行时缺乏必要的历史数据。
• 虽然这个方法有些不足，但是仍然在电影、音乐、图书推荐应用中，取得成功。

（2）基于人口统计学的推荐机制

基于人口统计学的推进机制，是一种最易于实现的推荐方法。它根据用户的基本信息发现用户的相关程度，然后将相似用户喜爱的其他物品，推荐给当前用户。

简单来说就是根据一个人的喜好，推荐给另一个人。

• 具体来讲，系统对每个用户都有一个用户画像（Profile）的建模，这个画像包括用户的基本信息，比如年龄、性别等。然后，系统根据用户的画像计算用户的相似度。相似用户称为 近邻。
• 对于系统的新用户来讲，系统没有“冷启动”问题。因为它不使用用户对物品的喜好历史数据。
• 该方法不依赖于物品的数据，所以它是领域独立的。但是该方法过于粗糙，对品味要求较高的领域不适用，比如图书、电影、和音乐等领域，推荐效果不是很好。

（3）基于协同过滤的推荐

基于协同过滤的推荐，根据用户对物品或者内容的偏好，发现物品或者内容之间的相似性，或者发现用户之间的相似性，然后基于这些相似性进行推荐。

分为三个子类：

1、基于用户（User-Based）的协同过滤推荐

基于用户的协同过滤推荐，是根据用户对物品或者内容的偏好，发现与某个用户偏好相似的k个“邻近”用户（可以根据KNN算法进行计算），然后基于这k个“近邻”用户的历史偏好信息，为该用户进行推荐。

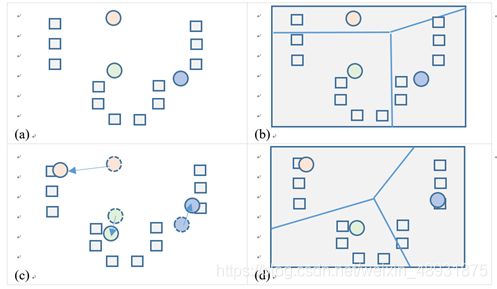
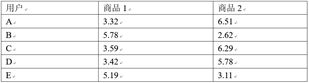
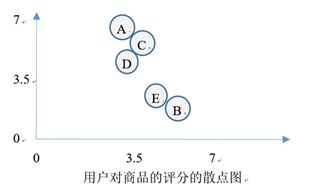
• 一个栗子：以电商领域为例，比如我们现在要给用户c进行商品推荐。我们首先进行用户间相似度的计算。发现用户C和用户D和E的相似度较高，也就是用户D和E是用户C的"K最近邻"。于是，我们可以给用户C推荐用户D和E浏览或者购买过的商品。需要注意的是，我们只需要推荐用户C还没浏览过或者还没购买过的商品即可，对于用户C浏览或者购买过的商品，无需重复推荐。

由图可以看出，用户ACD距离较近，用户BE距离较近。

2、基于项目（Item-based）的协同过滤推荐

基于项目的协同过滤推荐，是使用所有用户对物品或者内容的偏好信息，发现物品和物品之间的相似度，然后根据用户的历史偏好信息，将类似的物品推荐给用户。

• 一个栗子：还是以电商为例，当需要对用户C基于商品3进行商品推荐时，首先寻找商品3的“k最近邻”，也就是和商品3相似的商品，比如商品3的k最近邻为商品4和商品5.然后计算商品4、5与其他商品的相似度，并且进行排序，然后给用户C推荐新的商品，也就是用户C没有浏览或者购买过的商品。

3、基于模型（Model-based）的协同过滤推荐

基于协同过滤推荐机制的优势：

它是应用最为广泛的推荐机制。

1. 它无需对用户、物品进行严格的建模，它是领域无关的。
2. 该方法支持用户发现潜在的兴趣偏好。

基于协同过滤推荐的一些问题：

1. 该方法基于历史数据做出推荐，对新用户和新物品存在“冷启动”问题。
2. 推荐效果依赖于用户历史偏好数据的数据量及其准确性。
3. 少部分人的错误偏好，可能会对推荐的准确性产生很大的影响
4. 不能照顾特殊偏好和品味的用户，不能给予精细的推荐。

2.7、KNN（K邻近）算法

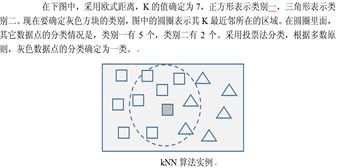
KNN（Near Neighbors）算法是一种分类算法。它根据某个数据点周围的最近K个邻居的类别标签情况，赋予这个数据点一个类别。

具体过程：

给定一个测试数据点，计算它与数据集中其他数据点的距离；找出距离最近的K个数据点，作为该数据点的近邻数据点集合；根据这k个近邻所归属的类别，来确定当前数据点的类别。

优点：

• KNN算法容易理解，也容易实现，它无需进行参数估计，也无需训练过程，有了标注数据之后，直接进行分类即可。
• KNN分类算法的应用非常广泛，人们把它应用到协同过滤推荐（collaborative filtering）、手写体识别等领域。

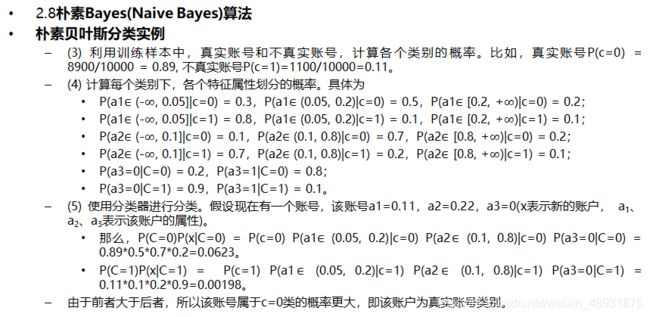
2.8、朴素贝叶斯（Bayes（Naive Bayes））算法

1、贝叶斯定理

P(B|A)表示在事件A已经发生的前提下，事件B发生的概率，称为事件A发生情况下，事件B发生的“条件概率”。

具体形式：

2、朴素贝叶斯分类

朴素贝叶斯分类是运用上述贝叶斯定理，并且假设特征属性是条件独立的一种分类方法，即朴素贝叶斯分类器假设样本的每个特征与其他特征都不相关。

3、贝叶斯分类实例

2.9、AdaBoost算法

Boost算法系列的思想，来自于PAC可学习型理论。该理论研究什么时候一个问题是可被学习的，以及可学习问题的具体学习方法。

• Valiant和Kearns首次提出了PAC学习模型中弱学习算法和强学习算法的等价性问题，即任意给定仅比随机猜测稍微好一点的弱学习算法，是否可以将其提升为强学习算法？如果二者等价，那么只需要找到一个比随机猜测略好的弱学习算法，就可以将其提升为强学习算法，而不必寻找很难获得的强学习算法。
• AdaBoost，是英文“Adaptive Boosting”（自适应增强）的缩写，由Yoav Freund和Robert E. Schapire在1995年提出，回答了上述问题。他们利用AdaBoost算法，把多个不同的决策树用一种非随机的方式组合起来，表现出惊人的性能。首先，决策树的准确率大大地提高了，可以与SVM媲美。其次，运行速度快，且基本不用调参数。最后，该组合分类器几乎不产生过度拟合Over Fitting。
• Boosting算法是一种把多个分类器整合为一个分类器的方法。

（1）整个AdaBoost迭代算法的主要三个步骤：

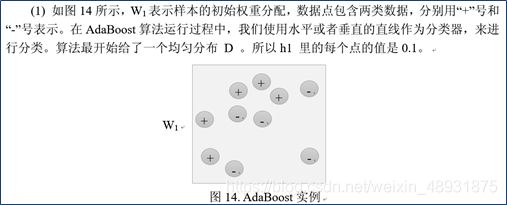
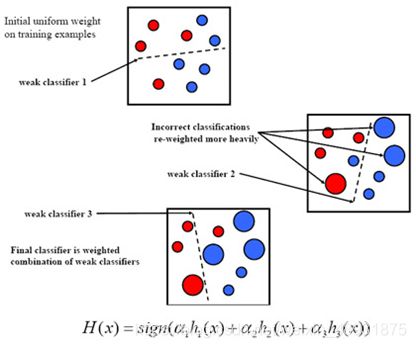
1. **初始化训练数据的权值分布。**如果有M个样本，则每一个训练样本最开始时都被赋予相同的权值：1/M。
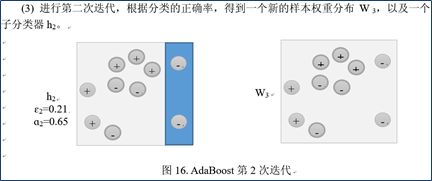
2. 训练弱分类器。在训练过程中，如果某个样本点已经被准确地分类，那么在构造下一个训练集中，他的权值就被降低；相反，如果某个样本点没有被准确地分类，那么它的权值就得到提高。在第t轮训练结束后，根据得到的弱分类器ht的性能，计算该分类器对应的权值at。并由ht的在训练集上的分类结果对权重向量Wi->Wi+1进行更新，接着，权值更新过的样本集被用于训练下一个分类器，整个训练过程如此迭代地进行下去。
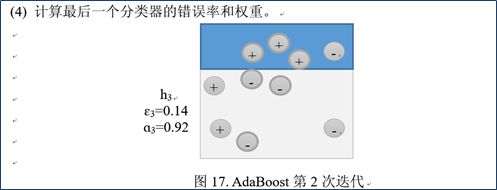
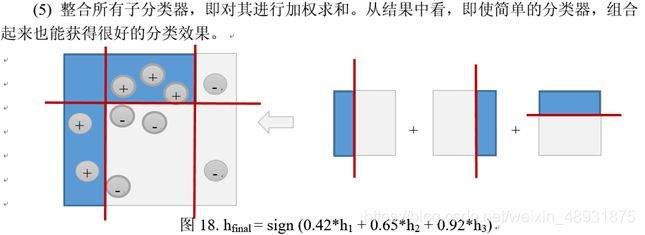
3. **将各个训练得到的弱分类器组合成强分类器。**各个弱分类器的训练过程结束后，加大分类误差率小的弱分类器权重，使其在最终的分类函数中起着较大的决定作用，而降低分类误差率大的弱分类器的权重，使其在最终的分类函数中起着较小的决定作用，换而言之，误差率低的弱分类器在最终分类器中占的权重较大，否则较小。

（2）AdaBoost算法思想

AdaBoost是一种迭代算法，其核心思想是针对同一个训练集训练不同的分类器，即弱分类器，然后把这些弱分类器集合起来，构造一个更强的最终分类器。

（3）AdaBoost算法的特点

AdaBoost是一种有很高精度的分类器，其算法具有如下特点：

1. 可以使用各种方法构建子分类器，AdaBoost算法提供对其进行组合以及提升的框架。
2. 当使用简单分类器时，计算出的结果是可以理解的。
3. 弱分类器构造及其简单，无需做特征筛选。
4. AdaBoost算法简单，不用调整分类器，不会导致Over Fitting，即过度拟合。

（4）AdaBoost算法的应用

1. 用于二值分类或多分类的应用场景。
2. 用于特征选择（Feature Selection）。
3. 无需变动原有分类器，而是通过增加新的分类器，可以提升分类器的性能。

（5）AdaBoost算法的实例

2.10线性回归、Logistic回归

（1）线性回归与多元线性回归

回归分析是应用广泛的统计分析方法，用于分析事物之间的相关关系。

• 一元线性回归模型，指的是只有一个解释变量的线性回归模型。
• 多元线性回归模型则是包含多个解释变量的线性回归模型。
• 所谓的解释变量就是自变量，而被解释变量就是因变量。
• 回归模型就是描述因变量和自变量之间依存的数量关系的模型。

一元线性回归模型具有y=ax+b的简单形式，a称为自变量x的系数，b称为截距，y=ax+b对应到图形，则是二维平面上的一条直线。扩展到多元线性回归模型，其形式为y=∑1_(i=1)^n▒〖a_i x_i 〗+b，方程中包含n个自变量x1, x2, …, xn，其系数分别是a1, a2, …, an。

注：建立多元线性回归模型的目的，是解释数据以及进行预测。

（2）多元线性回归模型的检验

• 多元线性回归模型建立以后，需要从几个角度进行检验，以了解模型的解释能力和预测能力。这些检验包括拟合优度检验、回归方程显著性检验、回归系数的显著性检验。
• 我们把因变量的总变差（SST），分解成自变量变动引起的变差（SSR），和其他因素造成的变差（SSE）。–用数学语言来表达为∑1▒〖(y-y ̅)〗^2 =∑1▒〖(y ̂-y ̅)〗^2 +∑1▒〖(y-y ̂)〗^2 =SSR+SSE，其中，y ̅表示样本均值，y ̂ 表示模型预测值，y表示因变量的实际值。

1、拟合优度检验

回归方程的拟合优度指的是，回归方程对样本的各个数据点的拟合程度。

拟合优度的度量一般使用判定系数**R^2**。R2越大，方程的拟合程度越高。

R^{2的计算公式为**R}2=SSR/SST=1-SSE/SST**。当一个多元线性回归模型，其判定系数接近1.0，说明其拟合优度较高。

2、回归方程显著性检验

回归方程的显著性检验，目的是评价所有自变量和因变量的线性关系是否密切。常用F检验统计量进行检验，F检验是对模型整体回归显著性的检验。F统计量的计算公式为F=(SSR/k)/(SSE/(n-k-1)),n为样本容量，k为自变量个数。

• 在给定的显著性水平（一般选0.05）下，查找自由度为（K，n-k-1）的F分布表，得到相应的临界值Fa，如果上述计算公式算得的F>Fa，那么回归方程具有显著意义，回归效果显著。否则，F

3、回归系数的显著性检验

使用t检验，分别检验回归模型中的各个回归系数是否具有显著性，以便使模型中只保留那些对因变量有显著影响的因素。t检验是对单个解释变量回归系数的显著性检验。

（3）共线性检验

所谓共线性，指的是自变量之间存在较强的线性关系，这种关系如果 超越 了因变量与自变量的线性关系，那么回归模型就不准确了。在多元线性回归模型中，共线性现象无法避免，只要不太严重就可以了。

• –计算自变量之间的相关系数矩阵的特征值的条件数k=λ_1/λ_p(λ_1为最大的特征值，λ_p为最小的特征值)。如果k<100，表示自变量之间不存在严重的共线性。如果100<= k <= 1000，那么自变量之间存在较强的共线性。如果k>1000，则自变量之间存在严重的共线性。降低共线性的办法，主要是转换自变量的取值，比如变绝对数为相对数或者平均数，或者更换其它的自变量。

（4）自变量筛选法

在多元线性回归中，还存在一个自变量选择问题，因为并不是所有的自变量都对因变量有解释作用。

变量选择的方法，包括前向筛选法、后向筛选法、和逐步筛选法三种。

1、前向筛选法

自变量不断进入回归方程的过程。选择与因变量具有最高相关系数的自变量进入方程，并进行各种检验。其次，在剩余的自变量中寻找偏相关系数最高的变量进入回归方程，并进行检验。反复上述步骤，直到没有可进入方程的自变量为止。回归系数检验的概率P值小于Pin(0.05)，才可以进入方程。

2、后向筛选法

自变量不断剔除出回归方程的过程。首先，将所有自变量全部引入回归方程。其次，在一个或多个t值不显著的自变量中，将t值最小的那个变量剔除出去，并重新建立方程和进行检验。回归系数检验值大于Pout(0.10)，则剔除出方程。如果新方程中所有变量的回归系数t值都是显著的，则变量筛选过程结束。否则，重复上述过程，直到没有变量可剔除为止。

3、逐步筛选法

是“前向筛选法”和“后向筛选法”的结合。前向筛选法，只对进入方程的变量的回归系数进行显著性检验，而对已经进入方程的其它变量的回归系数不再进 行显著性检验。也就是，变量一旦进入方程就不会被剔除。随着变量的逐个引进，由于变量之间存在着一定程度的相关性，使得已经进入方程的变量其回归系数不再显著，因此会造成最后的回归方程可能包含不显著的变量。逐步筛选法则在变量的每一个阶段都考虑的剔除一个变量的可能性。

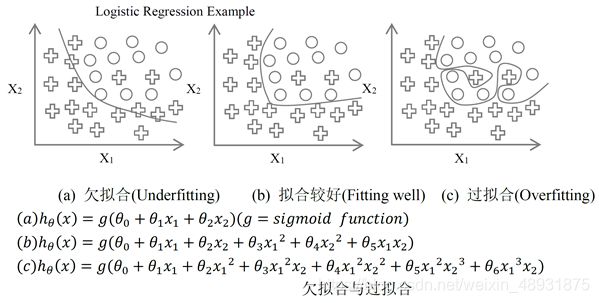
（5）Logistic回归

Logistic回归，实际上是一种分类方法，主要用于二分类问题。Logistic回归与多元线性回归，有很多相同之处，最大的区别是他们的 因变量不同 。两者可以归于同一个模型家族，即广义线性回归模型（Generalized Linear Model）。这一家族的模型，形式类似，即样本特征的线性组合，不同的是他们的因变量。

• 如果因变量是连续的，就是多元线性回归。
• 如果因变量是二项分布，就是Logistic回归。
• 如果因变量是Poisson分布，就是Poisson回归。
• 如果因变量是负二项分布，就是负二项回归。

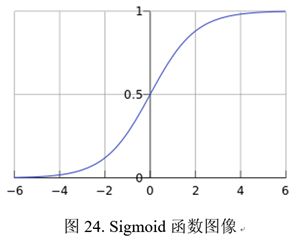
为了了解Logistic回归，需要首先了解Logistic函数（称为Sigmoid函数）。其函数形式为g(z)=1/(1+e^(-z) )。这个函数的自变量的变化范围是(-∞,+∞)，函数值的变化范围是[0,1]。

欠拟合和过拟合

2.11神经网络与深度学习（Neural Network and Deep Learning）

简说：人工神经网络是模仿动物和人类神经系统特征，进行分布式并行信息处理的数字模型。通过把大量人工神经元节点（感知机）连接起来，形成神经网络，并且利用训练数据调整优化节点间的连接强度，从而达到对新数据进行处理（分类、预测等）的目的。

1、神经元（感知机）

神经网络由“神经元”（或者称为感知机Perceptron）组成。在计算机里对神经元进行建模的时候，通过一个激活函数把神经元的输入映射到输出值。

激活函数：一般来讲，激活函数为一个非线性函数，目的是对实际应用中输出和输入之间的非线性关系进行建模。

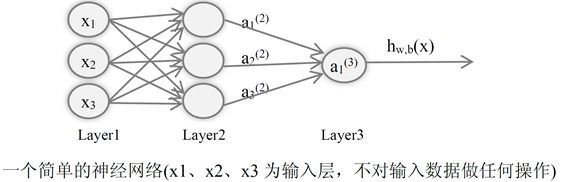
下图展示了一个简单的神经元。期中，x1、x2、x3为神经元的输入，神经元的输出通过hw,b(x)=f(∑1_(i=1)^3▒〖w_i x_i+b〗)函数来计算，这里f:R->R称为激活函数。

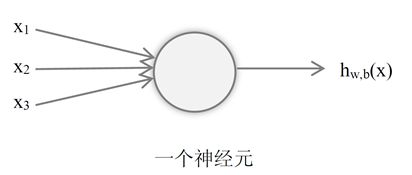
2、带一个隐藏层的简单神经网络

简说：简单神经网络是前馈神经网络（Feed Forward Neural Network ），在这个神经网络中，每一层的结点仅和下一层的结点相连。除了前馈神经网络外，另外一种类型的神经网络称为递归神经网络，它允许同一层节点相连或某一层的结点连到前面各层中的结点。在下文中，如果不做特殊说明，我们讨论的将是前馈神经网络。

• 神经网络就是由许多单一的神经元连接而成的网络结构，一个神经元的输出，可以是另外一个神经元的输入。
• 增加了一个隐藏层以后，神经网络系统不仅可以解决异或问题，而且具有非常好的非线性分类效果。但是当网络中各层的节点数增大，那么神经网络权重优化的计算量较大，没有很好的解决。

Layer1为输入层、Layer2为隐藏层、Layer3为输出层。

3、前向传播

**计算输出值的过程称为前向传播。**在前向传播过程中，每个神经元首先把上一层各个神经元获得的数值进行加权（每个连接的权重）求和，然后应用激活函数，获得相应的输出，然后通过与下一层的连接传播给下一层的各个神经元，直到获得最后的输出。

–Wij(l)表示第l层第j单元与第l+1层第i单元之间的连接参数，也就是连接线上的权重，bi(l)表示第l层第i单元的偏置项，也就是激活函数的常量部分。ai(l)表示第l层第i单元的激活值(输出值)，当l=1的时候，ai(1)=xi。

–激活过程可以用如下的公式表示出来：

–〖a_1〗^((2) )=f(〖w_11〗^((1) ) x_1+〖w_12〗^((1) ) x_2+〖w_13〗^((1) ) x_3+〖b_1〗^((1) ) )

–〖a_2〗^((2) )=f(〖w_21〗^((1) ) x_1+〖w_22〗^((1) ) x_2+〖w_23〗^((1) ) x_3+〖b_2〗^((1) ) )

–〖a_3〗^((2) )=f(〖w_31〗^((1) ) x_1+〖w_32〗^((1) ) x_2+〖w_33〗^((1) ) x_3+〖b_3〗^((1) ) )

–h_(w,b) (x)=〖a_1〗^{((3))=f(〖w_11〗}((2) ) 〖a_1〗^((2) )+〖w_12〗^((2) ) 〖a_2〗^((2) )+〖w_13〗^((2) ) 〖a_3〗^((2) )+〖b_1〗^((2) ))

4、反向传播（Back Propagation）训练方法

神经网络的权重，使用一种称为反向传播的方法，进行训练。

该算法与1986年由Rumelhar 和 Hinton 等人提出，该方法解决了带隐藏层的神经网络优化的计算量问题，使得带隐藏层的神经网络走向真正的实用。

形象的描述：反向传播算法，开始在输入层输入特征向量，经过神经网络各个隐藏层的层层计算获得输出，输出层发现输出和正确的输出（训练数据的输出部分）不一样，这时它就让最后一层神经元进行参数调整。最后一层神经元不仅自己调整参数，还会要求连接它的倒数第二层神经元调整连接权重，并且逐层往回退，调整各个神经网络层间的连接的权重。

5、神经网络小结

神经网络模仿了动物和人类神经系统的行为特性，经过训练的神经网络能够对非线性关系进行建模，在分类和预测方面获得了较好的性能。1986年反向传播算法解决了训练效率问题后，神经网络被应用到语音识别、图像识别、自动驾驶等多个领域，也获得了较好的效果。

• 但是上述神经网络存在若干的问题。首先，尽管使用了BP算法，一次神经网络的训练仍然耗时太久，而且训练过程可能导致局部最优解问题，这使得神经网络的优化较为困难。此外，隐藏层的节点数需要根据应用调整，节点数设置的多少，会影响到整个模型的效果，在实际应用中带来不便。
• 上个世纪90年代中期，Vapnik等人发明了SVM(Support Vector Machines，支持向量机)技术。SVM在若干个方面，体现出了比神经网络更大的优势，比如无需调整参数，训练和执行效率高，可以获得全局最优解。SVM在20世纪90年代到21世纪初，迅速代替神经网络，成为更加流行的机器学习算法，直到深度学习技术的崛起。

6、深度学习

深度学习是21世纪初流行起来的机器学习方法，它依赖于更深层次的神经网络。深度学习在图像识别、语音识别、自然语言处理、机器人等领域，获得了超过传统机器学习方法的性能。

1、深度学习能够流行起来的原因

• 大数据集的积累
• 计算机运算能力的提高
• 深度学习训练算法的改进
• 深度学习模型具有能够自主从数据上学习到有用的特征等
• 人们找到了提高深度神经网络模型训练效率的方法。

2、深度学习例子

• Alpha Go围棋程序

3、深度学习可以自动识别样本的特征

深度神经网络可以做自动识别样本的特征。这一点，使得深度学习在一些不知如何设计有效的特征的应用场合，比如图像识别和语音识别等，获得了很好的性能。**在神经网络中，浅层的神经元学习到初级的简单的特征，馈入下一层神经网络，深层的神经元在前一层神经元识别到的特征的基础上，学习到更加复杂的特征。**这个过程在相邻的神经网络层间重复，各个神经网络层学习到不同抽象级别的特征，越是靠后的神经网络层，学习到更加抽象的特征，最后完成预定的识别任务，比如语音识别和图像识别。

一个栗子：

比如在图像识别中，

• 第一个隐藏层学习到的是“边缘”的特征
• 第二个隐藏层学习到的是由“边缘”组成的“形状”的特征。
• 第三个隐藏层学习到的是由“形状”组成的“图案”的特征
• 最后的隐藏层学习到的是由“图案”组成的“对象”的特征等。

隐藏层：是神经网络对训练数据进行内部抽象表示的结构，就像人脑对现实世界的对象有一个内部表示一样。在神经网络里增加隐藏层，使得后续的隐藏层可以在前导隐藏层的内部表示的基础上，建立新的抽象级别的内部表示。

可以说，深度模型是技术手段，特征学习是目的。

4、与传统的浅层学习对比

深度学习的不同之处在于：

1. 强调模型结构的深度，深度神经网络通常有5层、6层，甚至超过10层的隐藏层
2. 突出特征学习的重要性，通过逐层的特征变换，将不同抽象级别的特征识别出来，最后是的分类和预测更加容易。

5、深度学习的应用

• 深度学习的应用非常广泛，包括图像/视频的识别、语音识别、自然语言处理等。
• 在图像和视频应用方面，深度学习模型可以识别照片中的物体，对照片进行自动分类和搜索，比如Google Photo、百度识图、淘宝拍立得等，都使用了深度学习模型。深度学习模型应用于自动驾驶系统，对人员、车辆等路况信息进行识别和追踪，进而做出有效的应付。深度学习模型还可以用于人脸识别，实现刷脸支付等功能，为人们的生活带来方便。
  • 一个栗子：–2014年，Google试图利用深度学习技术，从图像直接生成一段自然语言的描述。Google把两个深度神经网络结合起来(卷积神经网络CNN和循环神经网络RNN)，组成一个模型，完成这个任务。其中一个神经网络负责图像识别，另外一个神经网络负责语言生成。图28展示了他们使用的网络结构。这个网络结构，基于左边的图片，生成了右边的文字描述。

6、深度学习的局限性

• 深度学习技术并非万能的技术，人们不应对其过于迷信，它学习到的可能是数据中的相关关系，但不一定是因果关系。深度学习的能力很强，但是和我们预期的真正的人工智能相比，仍然缺乏必要的能力，比如逻辑推理能力，集成抽象能力。所以深度学习可以看作是实现人工智能的一种途径，而不是终极解决方案。
• 在工程实践中，把深度学习技术和其他机器学习技术结合起来，比如贝叶斯推理和演绎推理等技术，互相取长补短，是一个哟前途的策略。比如，深度学习技术可以和增强学习技术相结合，所谓增强学习，是指计算机通过与环境交互，从中得到的奖赏和惩罚，进而自主学习更优的策略。

7、深度神经网络的基础模块和网络模块

深度神经网络的基本模块，包括Autoencoder、Restricted Boltzmann Machines等。

不同的神经网络模型，包括CNN、DBN、RNN、LDTM等。

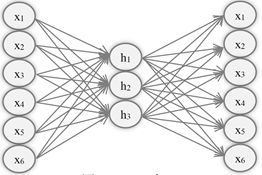
（1）Autoencoder（自动编码器）

通常来讲，一个Autoencoder就是一个前向反馈的简单神经网络，它的目的是从训练数据上学习一个经过压缩的简洁的数据的表示、或者简洁的一个编码。

• 为了达成这个目的，输入层和输出层的节点数是一样的，预期的输出就是训练数据本身，而隐藏层的节点数，大大少于输入层（或者输出层的节点数）。
• 这个网络的目的，不是让其学习到输入数据和预期结果（分类标签/或者预测值）之间的一个映射，而是学习到一种数据特征或者内部表示的结构。于是，隐藏层也叫做特征检测器。

（2）Restricted Boltzmann Machines（RBM，受限玻尔兹曼机）

标准的玻尔兹曼机，由可见单元层（Visible Layer，扮演输入/输出层）以及隐藏层（Hidden Layer）构成。可见单元层和隐藏层的单元之间是双向全联通的，也就是数据可以从可见层的单元传播到隐藏层的单元，也可以从隐藏层的单元传播到可见单元层的单元；可见单元层的每个单元和隐藏层的每个单元之间都有连接。

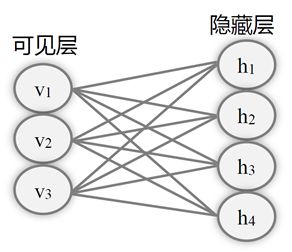
• 如果可见单元层和隐藏层的单元不是全联通的，这样的玻尔兹曼机称为受限玻尔兹曼机。一般来讲，各个单元的激活函数产生0或者1，这些0/1输出符合伯努力分布。
• 这个算法，使得神经网络学习到对输入数据如何进行内部表示，然后用这些内部表示重新生成数据。如果重新生成的数据和实际数据还未达到足够的接近，那么该网络进行权重的调整，然后接着尝试。
• RBM采用一种称为对比分歧（CD，Contrastive Divergence）的方法进行训练。

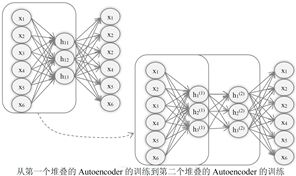
（3）堆叠的自动编码器（Stacked Autoencoders）

• Autoencoder 可以堆叠起来，构成一个深度网络。在堆叠的Autoencoder构成的深度网络里，隐藏层t的输出，作为隐藏层t+1的输入，而第一个隐藏层的输入，就是整个网络的输入，也就是训练数据集的输入数据。
• 这样的深度网络可以每次一层地进行训练，解决传统反向传播（BP）算法带来的梯度消失（Vanishing Gradient）问题和过度拟合问题。
  • 梯度消失问题是指当我们在神经网络中加入更多的隐藏层的时候，反向传播过程很难把修正信息传播回前面的隐藏层，本应用于修正模型参数的误差随着层数的增加而指数递减，相对于各个隐藏层之间的连接的权重来讲，开始变得很小，这导致了模型训练的效率低下，无法获得好的训练模型。
  • 而过度拟合，则是训练出来的模型对训练数据拟合过度，但是当用这个模型来对新的数据进行分类和预测时，模型表现就不是很好，也就是缺乏泛化能力。近年来出现了新的实践上非常有效的正则化方法提高模型泛化能力，比如Dropout和Drop Connect，以及数据扩增技术等。
• 把Autoencoder 堆叠起来的深度网络，具有更加强大的分类和预测能力，获得令人印象深刻的结果。
• 预训练(pre-training)过程初始化了网络的各个层次连接的权重，从而让我们获得了一个复杂的多层的神经网络，再经过进一步的训练(Fine Tuning)就可以获得最后的模型。
• 分层预训练相当于对输入数据进行逐级抽象，类似大脑的认知过程。1958年，David Hubel 和Torsten Wiesel 发现了一种被称为“方向选择性细胞”(Orientation Selective Cell)的神经元细胞。当瞳孔发现了眼前的物体的边缘，而且这个边缘指向某个方向时，这种神经元细胞就会活跃。

（5）深度信念网络（DBN，Deep Belief Network ）

就像堆叠Autoencoder一样，我们也可以堆叠RBM，堆叠RBM构成的网络，称为深度信念网络。在这种情况下，第t个堆叠的RBM的隐藏层，作为第t+1个堆叠的RBM的可见层。而第一个堆叠的RBM的输入层，就是整个网络的输入层。

• 对深度信念网络，使用逐层贪心预训练算法进行训练。
  • 当单层RBM被训练完毕后，另一层RBM可被堆叠在已经训练完成的RBM上，形成一个多层模型。每次堆叠是，原有的多层网络输入层被输入训练样本，权重则是先前训练得到的权重，该网络的输出作为新增RBM的输入，新的RBM重复先前的单层训练过程。
  • 经过预训练后，我们得到一个层间连接的权重得到初始化的深度网络，接着可以使用反向传播算法进行精细调优。

（6）卷积神经网络（CNN，Convolution Neural Network）

**卷积神经网络是一种特殊类型的前向反馈神经网络，特别适合于图像识别、语音分析等应用领域。**卷积神经网络由于一个映射面上的神经元共享权值，因而减少了网络自由参数的个数，降低了网络参数选择的复杂度。该优点在网络的输入，避免了传统识别算法中复杂的特征提取过程。并且，在一个映射面生共享权值，使得图像的特征被检测出来，而不管它的位置是否发生移动。

• 卷积操作：卷积操作就是一个图像过滤器，它定义为对一个矩形图像区域进行加权操作。
• 比如，我们要对图像A进行卷积操作，产生图像B，卷积操作的过滤器为66的权重矩阵。那么B图像的<1,1>位置的像素的值，是A图像从<1,1>像素开始的矩形区域和66的权重矩阵的加权和(Weighted Sum)，而图像B的<1,2>位置上的像素的值，是A图像<1,2>像素开始的矩形区域和6*6的权重矩阵的加权和…等。
  

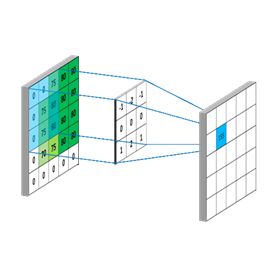
卷积神经网络的结构

卷积神经网络是一个多层的神经网络结构，各层为C层（Convolutional，卷积）或者S层（Subsampling，子采样）。

• 一般的，C层为特征提取层，S层是特征映射层，C层和S层交替组织起来。特征映射结构采用sigmoid函数作为激活函数，使得特征映射具有位移不变性，这点有利于图像的识别。
• 2011年以来，前馈神经网络深度学习中的常用方法就是，交替使用卷积层和最大值池化层（即子采样层）并加入单纯的分类层（即输出层）而构建。

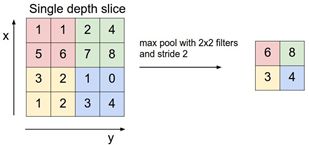
• S层用于对输入(图像)进行子采样。比如输入是32×32像素的图像，如果子采样的区域是2×2，那么输出将是16×16的图像，也就是说每４个(2×２)原图像的像素，被合并到输出图像的一个像素。子采样的方法很多，一般采用最大池化(Max Pooling)、平均池化(Average Pooling)、和随机池化(Stochastic Pooling)等。
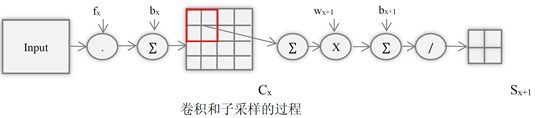
  • 图中展示了卷积和子采样的过程。其中，卷子过程包括，用一个可训练的滤波器fx去卷积一个输入的图像(第一阶段是输入的图像，后面的阶段就是卷积特征图了)，然后加一个偏置bx，得到卷积层Cx。卷积运算可以看作是从一个平面到另一个平面的映射。
  • 子采样过程包括，每邻域四个像素求和变为一个像素，然后通过标量Wx+1加权，再增加偏置bx+1，然后通过一个sigmoid激活函数，产生一个大概缩小四倍的特征映射图Sx+1。S层可以看作是模糊滤波器，它起到二次特征提取的作用。
  • 卷积神经网络的最后一个C层或者S层，通过全连接方式连接到输出层，输出层上输出分类标签或者预测值。

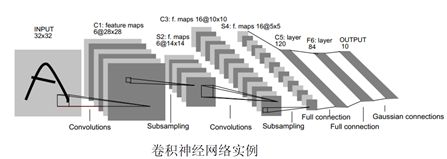
用于手写识别的LeNet-5

用于手写体(Digit Recognition)识别的LeNet-5是一个卷积神经网络，不算输入层，它一共有7层，每层都包含可以训练的连接权重。

–(1) 输入为32*32大小的图像。

–(2) C1层是一个卷积层，使用6个滤波器。C1层由6个特征图.Feature Map构成，特征图中每个神经元与输入中55的邻域相连，特征图的大小为2828。每个滤波器55=25个unit参数和一个bias参数，一共有(55+1)*6=156个可训练参数。

–(3) S2层是一个子采样层，对图像进行子抽样，可以减少数据处理量同时保留有用信息。S2层有6个1414的特征图。特征图中的每个单元与C1中相对应特征图的22邻域相连接。S2层每个单元的4个输入相加，乘以一个可训练参数，再加上一个可训练偏置，通过sigmoid函数计算结果。S2层有12个可训练参数。

（7）循环神经网络（Recurrent Neural Network）

对于自然语言处理、语言识别等应用，样本出现额的时间先后顺序非常重要，使用CNN神经网络进行分析不合适。在这样的应用场合，循环神经网络RNN是可行的方案。人们使用循环神经网络，来对时间关系进行建模。

• 上次隐藏层的输出，作为这一次隐藏层的输入，也就是一个神经元在时间戳t的输出，下一时刻戳t+1作为输入作用域自身。
• 直观来讲，这样做的目的是，希望让网络下一时刻的状态与当前时刻相关，即我们需要创建一个有记忆的神经网络。
  
  

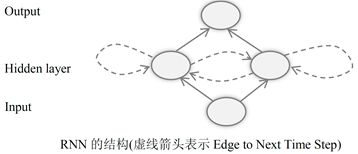
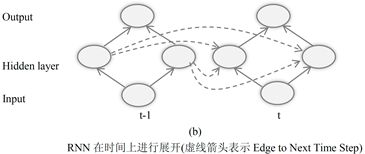
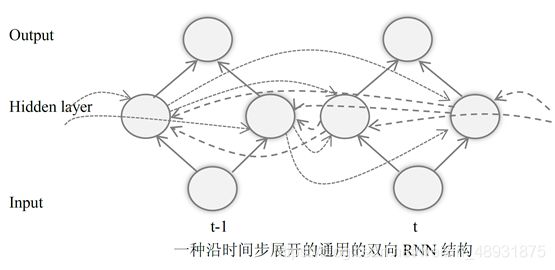
（8）双向RNN（Bidirectional Recurrent Neural Network，BRNN）

RNN通过参考历史信息，来对样本的时间关系进行建模。一个自然的问题是，RNN是否可以参考未来信息呢？答案是可以的，这就是双向RNN。

由图可以看出，其隐藏层同时使用历史和未来的信息进行预测。

（9）LSTM（Long Short Term Memory）网络

LSTM本质上是一种RNN。

• 在RNN训练的时候，往往会遇到严重的梯度消失问题。也就是误差梯度，随着事件的时间差的大小快速下降。这是发生在时间轴上的梯度消失。理想情况下，我们希望“所有历史”都对当前隐藏层的节点的预测产生作用。而实际上，这种影响只是维持了若干时间步。换一种说法，就是后面时间步额的错误信号，往往不能回到足够远的过去，想更早的时间步一样，影响网络，这使得神经网络难以学习远距离（时间上）的影响。
• LSTM模型很好的解决了这种梯度问题。
• 由于门控机制(gating mechanism)，Cell在工作时，可以保持较长一段时间的信息。并且在训练时，保护Cell内部的梯度，不受不利变化的影响，减少梯度消失效果。
• •一个Cell由三个门Gate(Input, Forget, Output)以及一个Cell单元(Cell Unit)组成。Gate使用Sigmoid激活函数，而Input和Cell State通常使用tanh函数来进行转换。
  
  

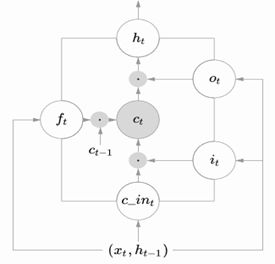
（10）双向LSTM结构

双向LSTM网络的目标和双向RNN是一致的，那就是它提供一种参考当前信息的较长时间段内的的历史、和未来信息(当前事件的更长时间段内的上下文环境)的机制。其网络结构和双向RNN类似，区别在于其基本构造单元换成了LSTM Cell。

RNN和LSTM的应用

–RNN和LSTM，以其强大的时间关系建模能力，被人们应用到很多场合。包括时间序列的预测(Time series prediction)、计算机音乐创作(Computer Composed Music)、节奏学习(Rhythm learning)、语法学习(Grammar learning)、机器翻译(Machine Translation) 、基于字符的 LSTM 语言模型(character-level language models)、语音识别(Speech Recognition)、自动给图像加描述(Image Captioning，也称为图文转换)、手写体识别(Handwriting recognition)、机器人控制(Robot control)、人体动作识别(Human action recognition)、蛋白质同源性检测(Protein Homology Detection)等。

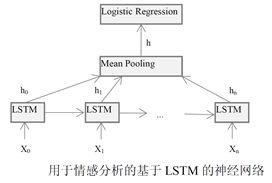
deeplearning.net网站提供了一个LSTM的应用教程，通过创建一个LSTM神经网络模型，实现对电影评论数据集(Movie Review Dataset)的情感分析(Sentiment Analysis)。这个模型由一个LSTM层、一个平均池化层、以及一个logistic回归层构成，如图所示。

三、主流数据深度分析工具

1. Mahout系统
2. Spark MLlib系统
3. Weka系统
4. R系统与语言系统
5. SPSS与MatLab
6. TensorFlow
7. Caffe

四、特征选择

1、简说

在机器学习中，特征选择起到至关重要的作用。特征选择的好，可以对数据量进行有效精简，提高训练速度，这点对于复杂模型来讲尤其重要。此外，特征选择，可以减少噪音特征，提高模型在测试数据集上的准确性，防止过拟合以及欠拟合情况的发生。

因为一些噪音特征，会导致模型出现错误的泛化，从而使得模型在测试集上表现较差。另外，从模型复杂度看，特征越多，模型越复杂，越容易发生过拟合的情况。常用的特征选择方法有互信息、信息增益、开放检验等方法。

2、方法

（1）信息增益法

信息增益法是根据某特征项为整个分类能够提供多少信息量，衡量该特征项的重要程度，从而决定对特征项的取舍。（为整体做了多少贡献，决定需不需要这个信息。）

某个特征项的信息增益：指的是有该特征或者没有该特征时，为整个分类所能提供的信息量的差别。其中，信息量的多少由熵来衡量。

（2）卡方检验法

卡方检验是统计学的基本方法。它的基本思想，是通过观察实际值与理论值（预期）的偏差，来决定理论的正确与否。

（3）互信息法

互信息用来评价一个事件的出现，对另一个事件的出现所贡献的信息量。

（对另一个事件的贡献）

ark MLlib系统
3. Weka系统
4. R系统与语言系统
5. SPSS与MatLab
6. TensorFlow
7. Caffe

四、特征选择

1、简说

在机器学习中，特征选择起到至关重要的作用。特征选择的好，可以对数据量进行有效精简，提高训练速度，这点对于复杂模型来讲尤其重要。此外，特征选择，可以减少噪音特征，提高模型在测试数据集上的准确性，防止过拟合以及欠拟合情况的发生。

因为一些噪音特征，会导致模型出现错误的泛化，从而使得模型在测试集上表现较差。另外，从模型复杂度看，特征越多，模型越复杂，越容易发生过拟合的情况。常用的特征选择方法有互信息、信息增益、开放检验等方法。

2、方法

（1）信息增益法

信息增益法是根据某特征项为整个分类能够提供多少信息量，衡量该特征项的重要程度，从而决定对特征项的取舍。（为整体做了多少贡献，决定需不需要这个信息。）

某个特征项的信息增益：指的是有该特征或者没有该特征时，为整个分类所能提供的信息量的差别。其中，信息量的多少由熵来衡量。

（2）卡方检验法

卡方检验是统计学的基本方法。它的基本思想，是通过观察实际值与理论值（预期）的偏差，来决定理论的正确与否。

（3）互信息法

互信息用来评价一个事件的出现，对另一个事件的出现所贡献的信息量。

（对另一个事件的贡献）