【回归预测】MATLAB 实现基于BP神经网络的多变量回归预测

简介：

人工神经网络是近年来发展起来的模拟人脑生物过程的人工智能技术。 它由大量的、同时也是很简单的神经元广泛互连形成复杂的非线性系统。具有自学习、自组织、自适应和很强的非线性映射能力，特别适合于因果关系复杂的非确定性推理、判断、识别和分类等问题。 在人工神经网络的实际应用中，常采用BP神经网络或它的变化形式。BP神经网络是一种多层神经网络，因采用BP算法而得名。通常采用软件来实现，主要应用于模式识别和分类、函数逼近、数据压缩等领域。

网络结构：

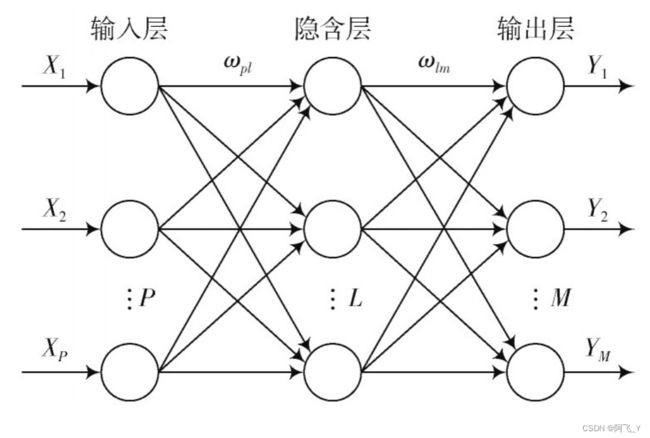
BP神经网络是一种多层前馈神经网络，由输入层、隐层和输出层组成。层与层之间采用全互连方式，同一层之间不存在相互连接，隐层可以有一个或多个。构造一个BP神经网络需要确定其处理单元--神经元的特性和网络的拓扑结构。神经元是神经网络最基本的处理单元，隐层中的神经元采用S型激活函数，输出层的神经元可采用S型或线性型激活函数。下图为一个典型的三层BP网络的拓扑结构。

 

算法原理：

神经网络学习采用改进BP算法，学习过程由前向计算过程和误差反向传播过程组成。在前向计算过程中，输入信息从输入层经隐层逐层计算，并传向输出层,每层神经元的状态只影响下一层神经元的状态。

设计BP神经网络的相关函数

（1）神经元激活函数:

         线性激活函数purelin、对数S型激活函数logsig、双曲线正切S型激活函数tansig。

（2）BP神经网络生成函数newff

        它是用来生成BP神经网络并进行初始化，可以确定网络层数、每层中的神经元数和激活函数。语法如下：

net = newff(P, T, S)
net = newff(P, T, S, TF, BTF, BLF, PF, IPF, OPF, DDF)

         newff 在确定网络结构后会自动调用初始化函数init，用缺省参数来初始化网络中各个权值和阈值，产生一个可训练的前馈网络,即该函数的返回值net。     

       P    : 输入矩阵（需归一化），每一列代表一个样本，每一行代表一个特征。

               输入层神经元节点数目 = 特征数目

       T    : 目标输出矩阵。每一列代表一个样本，每一行代表一维输出。

               输出层神经元节点数目 = 输出维度
　　S    : 隐藏层节点个数。通常节点个数介于特征数目和输出维度之间。[S1, S2, ..., SN]，                  可以设置多层隐藏层
　　TF  : 隐藏层的激活函数，默认隐含层为tansig函数，输出层为purelin函数。
　　BTF: BP神经网络学习训练函数，默认值为trainlm函数。
　　BLF: 权重学习函数，默认值为learngdm。
　　PF  : 性能函数，默认值为mse，可选择的还有sse，sae，mae，crossentropy。
　　IPF，OPF，DDF均为默认值即可。

（3）传递函数TF
　　  purelin：线性传递函数。
　　  tansig ：正切S型传递函数。
　　  logsig ：对数S型传递函数。　
　　  隐含层和输出层函数的选择对BP神经网络预测精度有较大影响，一般隐含层节点转移函数选用tansig函数或logsig函数，输出层节点转移函数选用tansig函数或purelin函数。
（4）学习训练函数BTF
　　  traingd：最速下降BP算法。
　　  traingdm：动量BP算法。
　　  trainda：学习率可变的最速下降BP算法。
　　  traindx：学习率可变的动量BP算法。
　　  trainrp：弹性算法。

（5）变梯度算法：
　     traincgf（Fletcher-Reeves修正算法）
　     traincgp（Polak_Ribiere修正算法）
　     traincgb（Powell-Beale复位算法）
　     trainbfg（BFGS 拟牛顿算法）
　     trainoss（OSS算法）

（6）初始化函数init：

         对网络的连接权值和阈值进行初始化。newff在创建网络对象的同时，自动调动初始化函数，根据缺省的参数对网络进行连接权值和阈值初始化。

（7）学习函数：

         提供多种学习函数,用来修正权值和阈值。基本的学习函数有：learngd、 learngdm。

（8）性能函数：
         用来计算网络的输出误差。为训练提供判据，包括:函数mae，计算网络的平均绝对误差；函数mse，计算网络的均方误差；函数 msereg，计算均方误差和权/阈值的加权；函数sse，计算网络的均方误差和。

（9）训练函数train:
         BP神经网络的训练初始化后，可对它进行训练。在MATLAB中训练网络有两类模式：逐变模式和批处理模式。在逐变模式中，每输入一个学习样本就根据网络性能指标函数对连接权值和阈值更新一次。在批处理模式中，所有的学习样本都学习完成后，连接权值和阈值才被更新一次。使用批处理模式不需要为每一层的连接权值和阈值设定训练函数，而只需为整个网络指定一个训练函数，使用起来相对方便，而且许多改进的快速训练算法只能采用批处理模式。训练网络的函数是train按设置的net.trainFcn和net.trainParam参数来训练网络，采用批处理方式进行网络的权值和阈值修正，最终达到设定的网络性能指标的要求。

（10）BP训练算法函数:

         根据网络的输入、目标期望输出，对由函数newff生成的BP神经网络进行计算，修正其权值和阈值，最终达到设定的网络性能指标的要求。不同的训练算法函数对应不同的训练算法，如traingd对应最基本梯度下降法；traingdm带有动量项的梯度下降法； traingdx带有采用动量项的自适应算法；用共轭梯度法进行训练的函数有：traincgf（采用Fletcher-Reeves搜索技术）、traincgp（采用Polak-Ribiers搜索技术）、traincgb（采用Powell-Beale搜索技术）；trainbfg是基于拟牛顿法的训练函数；trainlm是用Levenberg-Marquardt数值优化法来实现误差反传算法的。各算法的快慢及内存要求依问题的复杂程度、训练集大小、网络的大小及误差要求的不同而有所不同。一般来讲，对于含有几百个权重的网络，Levenberg-Marquardt算法有最快的收敛速度。该算法需要大的内存，可通过增大参数mem-reduc的值来减少内存的使用量。需要注意的是：减少内存使用量实际是通过将雅可比矩阵分解为一个个小的亚矩阵来实现的，每次只计算其中一个亚矩阵，这势必增加计算时间。所以，如果有足够的内存，应该将mem-reduc参数设为1，即每次都计算整个雅可比矩阵。拟牛顿算法的速度仅次于Levenberg-Marquardt算法而比共轭梯度法的速度快，内存的需要量也介于这二者之间。在共轭梯度法中，traincgb需要的内存数量最多，但通常也能最快收敛。总地来讲，基于共轭梯度法、拟牛顿算法和Levenberg-Marquardt法等数值优化算法的训练函数的效率比基于启发式算法的traingd、traingdm、traingdx的效率高。以上的训练算法函数均在网络生成函数newff中预先设置。

网络设计步骤

BP神经网络的实现有四个基本的步骤:

（1）网络建立：通过函数newff实现，它根据样本数据自动确定输入层、输出层的神经元数目；隐层神经元数目以及隐层的层数、隐层和输出层的变换函数、训练算法函数需由用户确定。

（2）初始化：通过函数init实现，当newff在创建网络对象的同时自动调动初始化函数init，根据缺省的参数对网络进行连接权值和阈值初始化。

（3）网络训练：通过函数train实现，它根据样本的输入矢量P、目标矢量T和预先已设置好的训练函数的参数对网络进行训练。

（4）网络仿真：通过函数sim实现，它根据已训练好的网络对测试数据进行仿真计算。

 代码实现过程：

%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行

%%  导入数据
res = xlsread('数据集.xlsx');

%%  数据分析
num_size = 0.7;                              % 训练集占数据集比例
outdim = 1;                                  % 最后一列为输出
num_samples = size(res, 1);                  % 样本个数
res = res(randperm(num_samples), :);         % 打乱数据集（不希望打乱时，注释该行）
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim;                  % 输入特征维度

%%  划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);

P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);

%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);

%%  创建网络
net = newff(p_train, t_train, 5);

%%  设置训练参数
net.trainParam.epochs = 1000;     % 迭代次数 
net.trainParam.goal = 1e-6;       % 误差阈值
net.trainParam.lr = 0.01;         % 学习率

%%  训练网络
net= train(net, p_train, t_train);

%%  仿真测试
t_sim1 = sim(net, p_train);
t_sim2 = sim(net, p_test);

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);

%%  均方根误差
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2 - T_test ).^2) ./ N);

%%  绘图
figure
plot(1: M, T_train, 'r-*', 1: M, T_sim1, 'b-o', 'LineWidth', 1)
legend('真实值','预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'训练集预测结果对比'; ['RMSE=' num2str(error1)]};
title(string)
xlim([1, M])
grid

figure
plot(1: N, T_test, 'r-*', 1: N, T_sim2, 'b-o', 'LineWidth', 1)
legend('真实值','预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'测试集预测结果对比';['RMSE=' num2str(error2)]};
title(string)
xlim([1, N])
grid

%%  相关指标计算
%  R2
R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test -  T_sim2)^2 / norm(T_test -  mean(T_test ))^2;

disp(['训练集数据的R2为：', num2str(R1)])
disp(['测试集数据的R2为：', num2str(R2)])

%  MAE
mae1 = sum(abs(T_sim1 - T_train)) ./ M ;
mae2 = sum(abs(T_sim2 -  T_test)) ./ N ;

disp(['训练集数据的MAE为：', num2str(mae1)])
disp(['测试集数据的MAE为：', num2str(mae2)])

%  MBE
mbe1 = sum(T_sim1 - T_train) ./ M ;
mbe2 = sum(T_sim2 -  T_test) ./ N ;

disp(['训练集数据的MBE为：', num2str(mbe1)])
disp(['测试集数据的MBE为：', num2str(mbe2)])

运行结果：

 

参考文献：

罗成汉.基于MATLAB神经网络工具箱的BP网络实现[J].计算机仿真,2004(05):109-111+115.