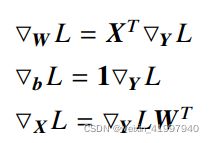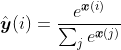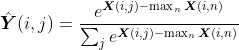三层神经网络实现手写数字图像分类

数据集采用MNIST。MNIST 数据集包含 4 个文件，分别是训练集图像、训练集 标记、测试集图像、测试集标记。每个样本都由灰度图像（即单通道图像）及其 标记组成，图像大小为 28 × 28。

完整代码见：

链接：https://pan.baidu.com/s/1t40bza30W8R58xZW5FbvVw 
提取码：cbmm

一、整体框架

设置五大模块，模块化，便于迭代。

1) 数据加载模块：从文件中读取数据，并进行预处理，其中预处理包括归一化、维度变换等处理。如果需要人为对数据进行随机数据扩增，则数据扩增处理也在数据加载模块中实现。

2) 基本单元模块：实现神经网络中不同类型的网络层的定义、前向传播计算、反向传播计算等功能。

3) 网络结构模块：利用基本单元模块建立一个完整的神经网络。

4) 网络训练（training）模块：该模块实现用训练集进行神经网络训练的功能。在已建立的神经网络结构基础上，实现神经网络的前向传播、神经网络的反向传播、对神经网络进行参数更新、保存神经网络参数等基本操作，以及训练函数主体。

5) 网络推断（inference）模块：该模块实现使用训练得到的网络模型，对测试样本进行预测的过程。

二、数据加载模块

首先根据MNIST的IDX文件格式进行数据的读取

    MNIST_DIR = "../mnist_data"
    TRAIN_DATA = "train-images-idx3-ubyte"
    TRAIN_LABEL = "train-labels-idx1-ubyte"
    TEST_DATA = "t10k-images-idx3-ubyte"
    TEST_LABEL = "t10k-labels-idx1-ubyte"

    def load_mnist(self, file_dir, is_images = 'True'):
        # Read binary data
        bin_file = open(file_dir, 'rb')
        bin_data = bin_file.read()
        bin_file.close()
        # Analysis file header
        if is_images:
            # 读取图像数据
            fmt_header = '>iiii'
            magic, num_images, num_rows, num_cols = struct.unpack_from(fmt_header, bin_data, 0)
        else:
            # 读取标记数据
            fmt_header = '>ii'
            magic, num_images = struct.unpack_from(fmt_header, bin_data, 0)
            num_rows, num_cols = 1, 1
        data_size = num_images * num_rows * num_cols
        mat_data = struct.unpack_from('>' + str(data_size) + 'B', bin_data, struct.calcsize(fmt_header))
        mat_data = np.reshape(mat_data, [num_images, num_rows * num_cols])
        print('Load images from %s, number: %d, data shape: %s' % (file_dir, num_images, str(mat_data.shape)))
        return mat_data

    def load_data(self):
        # TODO: 调用函数 load_mnist 读取和预处理 MNIST 中训练数据和测试数据的图像和标记
        print('Loading MNIST data from files...')
        train_images = self.load_mnist(os.path.join(MNIST_DIR, TRAIN_DATA), True)
        train_labels = self.load_mnist(os.path.join(MNIST_DIR, TRAIN_LABEL), False)
        test_images = self.load_mnist(os.path.join(MNIST_DIR, TEST_DATA), True)
        test_labels = self.load_mnist(os.path.join(MNIST_DIR, TEST_LABEL), False)
        self.train_data = np.append(train_images, train_labels, axis=1)
        self.test_data = np.append(test_images, test_labels, axis=1)

三、基本单元模块

 实现全连接、激活函数等层的定义、前向传播、反向传播等具体操作。

（1）采用三层神经网络，主体是三个全连接层。

（2）在前两个全连接层之后使用 ReLU 激活函数层引入非线性变换。

（3）在神经网络最后添加Softmax 层计算交叉熵损失。

同类型的层用一个类来定义，多个同类型的层用类的实例来实现，层中的计算用类的成员函数来定义（计算包括初始化、前向计算、反向计算、参数更新等）。

 3.1 全连接层

（1）层的初始化：输入神经元数量、输出神经元数量

（2）参数初始化：权重W和偏置b。在对权重和偏置进行初始化时，通常利用高斯随机数初始化权重的值，而将偏置的所有值初始化为0。

（3）前向计算：Y = XW + b

（4）反向计算：

关于几个式子可能有人会有疑问，到底是谁左乘谁，为什么莫名奇妙出了转置？

这个地方给一个我常用的分析办法：W矩阵是mxn，求导后依然为mxn，X为1Xm的，L对y的偏导为1xn的，因此使用X^T乘以L对y的偏导。

分析办法详细见：反向传播算法的矩阵维度分析 - 知乎

详细的推导见：神经网络的反向传播算法中矩阵的求导方法(矩阵求导总结)_ASR_THU的博客-CSDN博客_神经网络矩阵求导

 （5）参数更新：采用梯度下降法进行更新即可。

class FullyConnectedLayer(object):
    def __init__(self, num_input, num_output):  # 全连接层初始化
        self.num_input = num_input
        self.num_output = num_output
        print('\tFully connected layer with input %d, output %d.' % (self.num_input, self.num_output))
    def init_param(self, std=0.01):  # 参数初始化
        self.weight = np.random.normal(loc=0.0, scale=std, size=(self.num_input, self.num_output))
        self.bias = np.zeros([1, self.num_output])
    def forward(self, input):  # 前向传播计算
        start_time = time.time()
        self.input = input
        # TODO：全连接层的前向传播，计算输出结果
        self.output = np.matmul(self.input, self.weight) + self.bias
        return self.output
    def backward(self, top_diff):  # 反向传播的计算
        # TODO：全连接层的反向传播，计算参数梯度和本层损失
        self.d_weight = np.dot(self.input.T, top_diff)
        self.d_bias = np.sum(top_diff, axis=0)
        bottom_diff = np.dot(top_diff, self.weight.T)
        return bottom_diff
    def update_param(self, lr):  # 参数更新
        # TODO：对全连接层参数利用参数进行更新
        self.weight = self.weight - lr * self.d_weight
        self.bias = self.bias - lr * self.d_bias
    def load_param(self, weight, bias):  # 参数加载
        assert self.weight.shape == weight.shape
        assert self.bias.shape == bias.shape
        self.weight = weight
        self.bias = bias
    def save_param(self):  # 参数保存
        return self.weight, self.bias

3.2 ReLu激活函数

前向传播时，大于0则为x不变，小于0则为0。

反向传播求导为1。

class ReLULayer(object):
    def __init__(self):
        print('\tReLU layer.')
    def forward(self, input):  # 前向传播的计算
        start_time = time.time()
        self.input = input
        # TODO：ReLU层的前向传播，计算输出结果
        output = np.maximum(0, self.input)
        return output
    def backward(self, top_diff):  # 反向传播的计算
        # TODO：ReLU层的反向传播，计算本层损失
        bottom_diff = top_diff
        bottom_diff[self.input < 0] = 0
        return bottom_diff

3.3 SoftMax层

Softmax常用于多分类问题。假设 Softmax 损失层的输入为向量 x，维度为 k。其中 k 对应分类的类别数，如对手写数字 0 至 9 进行分类时，类别数 k = 10。

（1）前向传播：

在前向传播的计算过程中，首先对 x 计算 e 指数并进行行归一化，从而得 到 Softmax 分类概率。计算公式为：

在实际的实现中使用批量随机梯度下降算法，假设选择的样本量为 p，Softmax 损失层 的输入变为二维矩阵 X，维度为 p × k，X 的每个行向量代表一个样本。则对每个样本的激活值计算 e 指数并进行行归一化得到：

其中 X(i, j) 代表 X 中对应第 i 样本 j 位置的值。当 X(i, j) 数值较大时，求 e 指数可能会出现数值上溢的问题。因此在实际工程实现时，为确保数值稳定性，会在求 e 指数前先进行减最大值处理，此时计算公式变为：

在前向计算时，对 Softmax 分类概率取最大概率对应的类别作为预测的分类类别。

（2）损失函数：

损失函数层在计算前向传播时还需要根据真实值y计算总的损失函数值。在分类任务中， y 通常表示为一个维度为 k 的 one-hot 向量，该向量中对应真实类别的分量值为 1，其他值为 0。 

采用交叉熵损失函数：

 由于此时y是一个one-hot向量，上式应为：

（3）反向传播：

在反向传播的计算过程中，可直接利用标记数据和损失函数层的输出计算本层输入的损失（损失 是所有样本的平均损失，因此对样本数量 p 取平均）：

class SoftmaxLossLayer(object):
    def __init__(self):
        print('\tSoftmax loss layer.')
    def forward(self, input):  # 前向传播的计算
        # TODO：softmax 损失层的前向传播，计算输出结果
        input_max = np.max(input, axis=1, keepdims=True)
        input_exp = np.exp(input - input_max)
        self.prob = input_exp / np.sum(input_exp, axis=1, keepdims=True)
        return self.prob
    def get_loss(self, label):   # 计算损失
        self.batch_size = self.prob.shape[0]
        self.label_onehot = np.zeros_like(self.prob)
        self.label_onehot[np.arange(self.batch_size), label] = 1.0
        loss = -np.sum(np.log(self.prob) * self.label_onehot) / self.batch_size
        return loss
    def backward(self):  # 反向传播的计算
        # TODO：softmax 损失层的反向传播，计算本层损失
        bottom_diff = (self.prob - self.label_onehot) / self.batch_size
        return bottom_diff

四、网络结构模块

4.1 神经网络初始化

确定神经网络相关的超参数，例如网络中每个隐层的神经元个数。

def __init__(self, batch_size=100, input_size=784, hidden1=32, hidden2=16, out_classes=10, lr=0.01, max_epoch=1, print_iter=100):
    self.batch_size = batch_size
    self.input_size = input_size
    self.hidden1 = hidden1
    self.hidden2 = hidden2
    self.out_classes = out_classes
    self.lr = lr
    self.max_epoch = max_epoch
    self.print_iter = print_iter

4.2 建立网络结构

定义整个神经网络的拓扑结构，实例化基本单元模块中定义的层并将这些层进行堆叠。本实验使用的三层神经网络包含三个全连接层，并且在前两个全连接层后跟随有 ReLU 层，神经网络的最后使用了 Softmax 损失层。

def build_model(self):  # 建立网络结构
    # TODO：建立三层神经网络结构
    print('Building multi-layer perception model...')
    self.fc1 = FullyConnectedLayer(self.input_size, self.hidden1)
    self.relu1 = ReLULayer()
    self.fc2 = FullyConnectedLayer(self.hidden1, self.hidden2)
    self.relu2 = ReLULayer()
    self.fc3 = FullyConnectedLayer(self.hidden2, self.out_classes)
    self.softmax = SoftmaxLossLayer()
    self.update_layer_list = [self.fc1, self.fc2, self.fc3]

4.3 神经网络参数初始化

对于神经网络中包含参数的层，依次调用这些层的参数初始化函数，从而完成整个神经网络的参数初始化。本实验使用的三层神经网络中，只有三个全连接层包含参数，依次调用其参数初始化函数即可.

def init_model(self):
   print('Initializing parameters of each layer in MLP...')
   for layer in self.update_layer_list:
        layer.init_param()

五、网络训练模块

神经网络的训练模块通常拆解为若干步骤，包括神经网络的前向传播、神经网络的反向传播、神经 网络参数更新、神经网络参数保存等基本操作。

按照神经网络的结构依次进行实现即可。

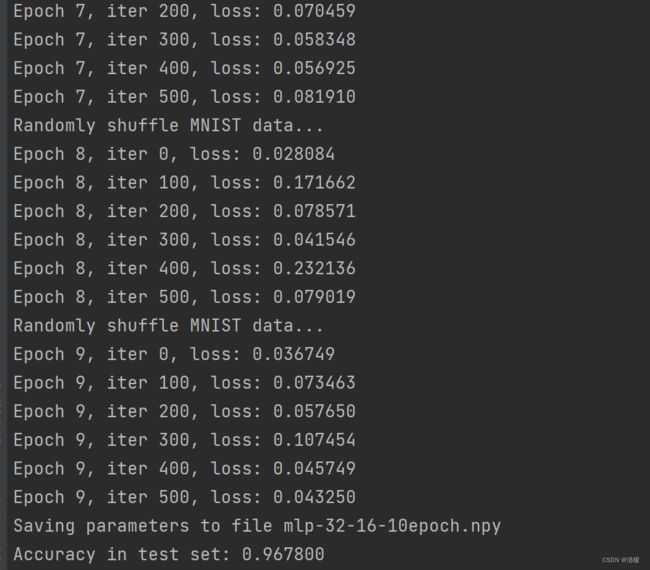
六、网络推断模块

调用训练好的网络模型，对测试数据进行预测，以评估模型的精度。

 运行结果：