Python元学习-通用人工智能的实现 第2章 阅读笔记

本书代码：https://github.com/sudharsan13296/Hands-On-Meta-Learning-With-Python
本书ISBN号：9787115539670

第1章：元学习

第2章：基于度量的单样本学习算法——孪生网络

2.1 什么是孪生网络

单样本学习在每个类别中只学习一个训练实例。孪生网络主要用于各类别数据点较少的应用中，它可以从较少的数据点中学习。

孪生网络大致上由两个对称的神经网络组成，它们具有相同的权重和架构，并在最后由能量函数E 连接在一起。

我们将图像 X1 提供给网络A，将图像 X2 提供给网络B。这两个网络的作用都是为输入图像生成嵌入（embedding），即特征向量（feature vector）。然后，我们将这些嵌入提供给能量函数，它会给出这两个输入的相似程度。能量函数基本上可以是任何相似性度量，如欧氏距离和余弦相似度。

2.1.1 孪生网络的架构

我们用欧氏距离作为能量函数，如果 X1 和 X2 相似，那么E 的值会较小。如果输入值不相似，那么E 的值会很大。

孪生网络的输入( X1 , X2 )应该成对出现，它们的二元标签（binary label）Y ∈{0,1}代表输入对是正样本对（genuine pair，相同）还是负样本对（imposite pair，不同）。

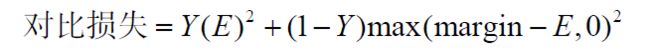
在上式中，Y 代表真实标签（true label），当两个输入值相似时为1，当两个输入值不相似时为0。E 是能量函数，它可以是任何距离度量。变量margin 用于保存约束，也就是说，当两个输入值不相似时，如果它们的距离大于margin 的值，那么就不会导致损失。
当 E < margin 时，此时Y=0，Loss = (margin-E)^2 ，神经网络以最小化该损失为目标，那么E就会朝着大于margin的方向优化，对于两个不相似的向量，距离越远越好

2.1.2 孪生网络的应用

签名验证任务的目标是识别签名的真实性，用正样本签名对和负样本签名对训练孪生网络，利用卷积网络从签名中提取了特征，然后通过测量两个特征向量之间的距离来识别相似性。当一个新的签名出现时，提取这些特征并将它们与存储的签名者特征向量进行比较，如果距离小于某个阈值，则接受签名是真实的，反之则拒绝签名。
存储各个类别样本的特征向量，然后用于对比特征

2.2 使用孪生网络进行人脸识别

孪生网络要求输入值成对并带有标签，必须以这种方式创建数据。我们从同一个文件夹中随机取出两张图像，并将它们标记为正样本对；从两个文件夹中分别取出一张图像，并将它们标记为负样本对。如图所示，正样本对的照片上是同一个人，而负样本对的照片上是不同的人。
正样本是同一类别，负样本是不同类别

我们将图像对中的一个图像输入网络A，另一个图像输入网络B（其实是同一个网络）。这两个网络的作用只是提取特征向量，然后把两个网络输出的特征向量输入能量函数，用于测量相似度（用欧氏距离作为能量函数）。因此，我们通过输入图像对来训练网络，以学习它们之间的语义相似度。

定义数据集
我们有20000 个数据点，其中10000 个是正样本对，其余的10000 个是负样本对，将正样本对与负样本对拼接成完整的数据：

X = np.concatenate([x_geuine_pair, x_imposite_pair], axis=0)/255
Y = np.concatenate([y_genuine, y_imposite], axis=0)

X.shape
(2000, 2, 1 ,56 ,46)
1*56*46 是图像通道和尺寸，2表示一对数据，2000是总数据对数

Y.shape
(2000, 1)

构建孪生网络
首先，定义基网络，它基本上是一个用于特征提取的卷积网络，将一张输入图像经过卷积得到特征图，然后flatten成长向量，经过两次线性函数（输出分别是128和50），最后得到一个长度为50的特征向量。
F1(x) = (1, 50)

把图像对输入基网络F1()，它将返回嵌入，即特征向量：
feat_vecs_a = F1(img_a)
feat_vecs_b = F1(img_b)

feat_vecs_a 和feat_vecs_b 是图像对的特征向量。接下来把这些特征向量输入能量函数，计算它们之间的距离，并使用欧氏距离作为能量函数：

def euclidean_distance(vects):
	x, y = vects
	return K.sqrt(K.sum(K.square(x - y), axis=1, keepdims=True))

接下来将损失函数定义为contrastive_loss 函数:

# y_true是标签，y_pred是每一对的距离
# K.maximum(margin - y_pred, 0) 表示当负样本的距离超过 margin 那么不再执行优化
def contrastive_loss(y_true, y_pred):
	margin = 1
	return K.mean(y_true * K.square(y_pred) + (1 - y_true) * K.square(K.maximum(margin - y_pred, 0)))

总结

数据集的构成：

算法总体流程：

思考

孪生网络的架构只适合判定两个类别事物的相似程度，无法同时对多个类别进行相似度判别