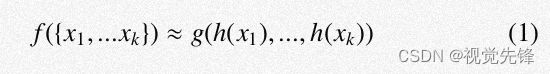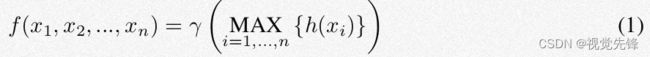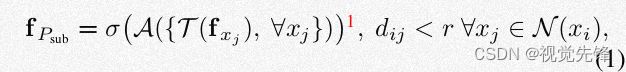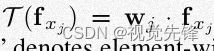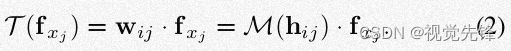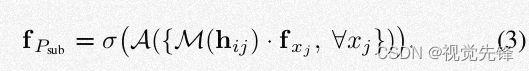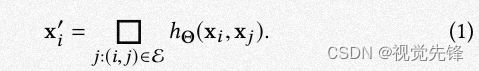基于点云的深度学习方法综述

        我们生活在一个三维世界里，自从1888年相机问世以来，三维世界的视觉信息就通过相机被映射到二维图象上。但是二维图像的缺点也是显而易见的，那就是缺少深度信息以及真实世界中目标之间的相对位置。所以这种数据表示方法不适合应用在机器人、自动驾驶、虚拟现实等对深度和位置有要求的领域中。为了捕捉到三维世界的深度信息，早期我们使用多目视觉的方法或者来自RGB－D的深度图提取三维空间信息。点云作为一种数据结构，蕴含着丰富的几何信息，我们可以用它表示多目相机和深度图中提取出来的3D信息。 
一、什么是点云？
      点云可以简单概括为空间中的一组数据点，一个场景中的点云是由在该场景中目标的表面所采样的一系列3D点组成的。
二、点云的主要特征有哪些？

      （1）直接特征表示

      XYZ 坐标：可以表示一个点的最直接的特征就是由传感器提供的XYZ坐标，它表示该点在现实世界坐标系下的实际位置。

      反射强度：代表着每种材料表面的反射属性，也是激光扫描器一种最常用的属性。不同的目标有不同的反射强度，因此在点云中的密度也有所不同。

      （2）“几何－局部”特征表示

      “几何－局部”特征包含着一个点和其临近点的空间关系，给定一个局部搜索区域，我们可以在该区域内通过临近点搜索算法对给定点的临近点进行搜索。最常用的两种临近点搜索算法分别是：K－近邻算法和球形算法。

      我们对定义在搜索区域的协方差矩阵进行分解，得到该矩阵的特征值和特征向量，我们用这两者表示“几何－局部”特征，常用的“几何－局部”特征包括以下三种：

      a.局部密度：局部密度主要取决于给定区域内点的数量。随着与传感器距离的增加，局部点的密度也在不断减小。在基于体素的模型当中，体素的尺寸决定了局部点密度的大小。‘

      b.局部法向量：它代表目标表面上特定点的法方向。

      c.局部曲率：某个点单位切向量的方向变化率。

      在过去几年里我们基于手动制造的特征处理点云，人工特征并不要求大规模的训练数据，但并未得到大规模使用，原因是并不包含充足的点云数据。随着硬件计算能力的提高，越来越多的深度学习处理方法相继问世，但仍面临诸多挑战。以下是对这些挑战的详细说明。

三、点云数据的挑战：

      不规则性：点云数据的不规则性归因于这些点并不是从某个场景或者目标上均匀采样的，有些区域的点比较稠密，有些区域的点相对稀疏，且各区域的强度也不尽相同。造成这一现象的原因是目标和雷达传感器的距离不同，除此之外，扫描时间和需要的分辨率也会影响分布和强度。

      非结构性：点云数据并不是规则的网格，在2D图像中，我们用均匀的网格表示像素，相邻像素之间的大小是固定的。然而，点云中的每个点是被独立扫描的，相邻点之间的距离并不固定。这一特性会使点云数据产生噪声，主要体现为，点云中的每个点除了以某一概率出现在某个半径的邻域内，还可能出现在空间中的一些随机位置，这种现象称为点的摄动，摄动会产生离群点。

      无序性：一个场景中的点云实际上是围绕该场景中的目标获得的一系列点，通常用XYZ坐标表示它们，然后被存储在一个文件的列表中。作为一个集合，集合中点的存储顺序并不影响场景的表示。
        不完整性：通过激光雷达采集的点云一般具有不完整性，可能的原因是目标之间的相互遮挡、城市场景中背景的聚簇部分以及材料表面反射率不理想。这样的现象在实时捕捉运动目标时尤为严重。
       类别混淆：在自然环境中，形状相似或者目标的反射性相近，会对点云中目标的检测和分类产生影响。
四、3D深度学习模型的挑战：
      序列和方向不变性：由于点云中的点没有固定的顺序和方向，对于一个由N个点构成的集群，要将N!种状态的序列投喂到网络中来维持序列不变性。同时，点集方向的丢失也为模式识别等任务带来很大挑战。
      刚性变换：许多点之间的刚性变换例如3D旋转和3D转换都会影响模型性能。
      大数据：在城市或者乡村的自然场景中，雷达可能收集数百万到数十亿的点。例如，在KITTI数据集中，3D雷达扫描器每帧可以捕捉100k个点，而最小的场景也要包含114个帧，这为点的存储带来了不小的困难。
      准确性：在自动驾驶中，对于道路目标的精确感知至关重要。然而，由于类内和类间目标的变化以及数据的质量为这种准确性造成了挑战。例如，同一类别的目标会有很多不同的实例，主要表现在材料、形状以及尺寸的变化。
      高效性：相比于2D图像的处理，处理大量点云数据会造成很高的计算量以及时间复杂度，因此如何提高计算效率也是自动驾驶领域中要克服的众多挑战之一。
四、处理点云的深度学习方法研究
1、基于结构化网格的学习
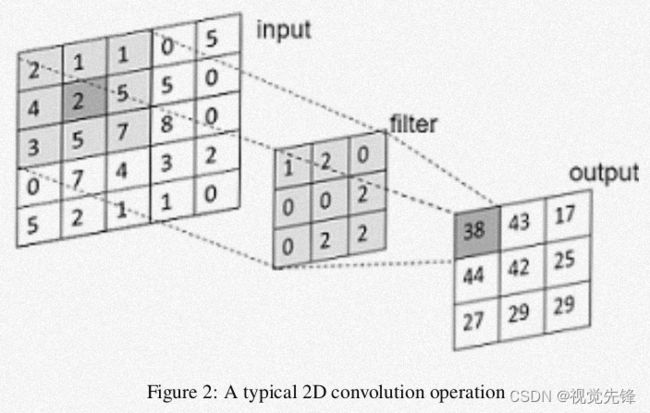
       深度学习，尤其是卷积神经网络的成功源于卷积操作。卷积操作主要用于特征提取，它要求卷积核的搜索区域是基于网格的。

 如果想对非结构化的点云数据实施深度学习的方法，我们首先想到的是将点云数据处理成结构化的形式，这样的方法通常分为两种：基于体素的方法和基于视图的方法。
2、基于体素的方法
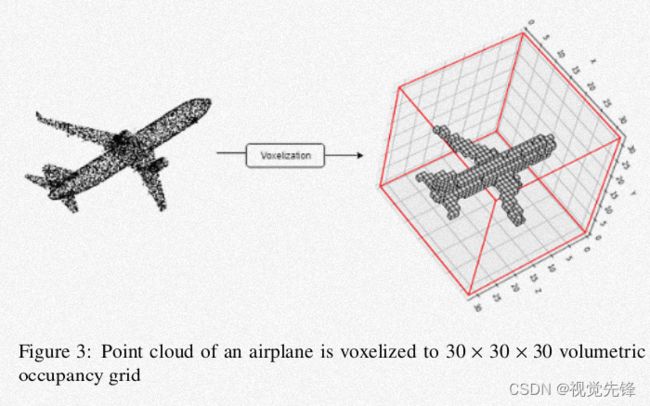
       对于2D图像上的卷积操作，我们选用一个大小为x × y的卷积核，对一个大小为X×Y的矩阵进行卷积操作（其中，x <= X，y <= Y）。在基于体素的方法中，我们用类似的操作进行卷积：首先将点云转化为大小是X×Y×Z的3D体素结构，然后用大小为x × y × z的3D卷积核对该体素结构进行卷积操作（其中，x <= X，y <= Y，z <= Z）。

 基于体素的深度学习方法大致分为两个步骤，首先对点云数据进行预处理，使其成为拥有固定大小的体素结构，我们称这一阶段为离线处理；其次在学习阶段，我们利用大量的3D卷积层，池化层以及全连接层设计神经网络，我们称这一阶段为在线学习阶段。
模型举例：3D Generative Adversarial Network(3D－GAN)
        生成对抗网络(GAN)于2014年问世，它由生成器和识别器两部分组成，识别器试图识别真实的目标和由生成器生成的目标，而生成器尽最大可能生成假目标以迷惑识别器。上述鉴别器和生成器的对抗过程，是一种所谓的极大极小游戏。鉴别器希望自己的鉴别能力达到最强，生成器希望使鉴别器的鉴别能力达到最弱。当这个游戏达到一种平衡状态时，称为纳什均衡。GAN的结构如下图所示：

       假设真实数据是一些实数，这些实数服从某种分布，比如正态分布，如下图所示：

黑色点表示真实数据的概率分布。假设只知道这些实数，不知道它们的真实分布。生成器通过将噪声（隐变量）z映射到实数空间的实数，可以生成一些实数x，实现表示生成实数服从的分布。生成实数的分布一开始和真实数据分布并不一致，但随着训练过程的不断迭代，生成数据G(z)的分布逐渐接近真实数据x的分布，鉴别其将生成的数据识别成真实数据的概率也不断提高，最终两者分布完全一致。
GAN的损失函数如下图所示：

3D－GAN：3D－GAN的结构如下图所示：

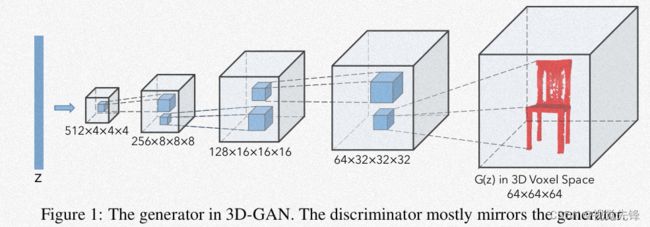对于一个从某个概率隐空间中随机采样的维度是200的隐向量z，生成器G将其映射成64×64×64的立方体，用以代表3D体素空间的目标G(z)。判别器输出的是一个置信度D(x)，用于判别输入到判别器的3D目标是真实的还是合成的。
        3D－GAN的损失函数是二分类交叉熵损失函数，用如下形式表示：

其中x是64×64×64体素空间中的真实目标，z是依概率p(z)随机采样的噪声向量，其每个维度都服从[0,1]均匀分布。
点评：
       基于体素的方法虽然表现出相对较好的性能，但由于体素的稀疏性，该方法需要消耗大量内存，这也会导致网络在大量非覆盖区域内进行卷积，从而造成大量不必要的计算。存储空间的消耗量一般受到体素分辨率的限制，一般只能在32^3 ~ 64^3之间，部分模型做了一些改进，但最多不能超过256^3。从图3也不难看出，随着提速分辨率的增长，内存消耗呈立方趋势增长。
3、基于多视图的方法
       这种方法将早已成熟的2D卷积神经网络的技术优势发挥到了3D任务中。由于图片其实是现实3D世界的一种表示，只是我们通过相机将3D世界压缩到了2D网格中，因此这一类别的方法将点云转化成了一系列图片，并在这些图片上应用2D卷积技术。
模型举例：Multi-View Convolutional Neural Network(MVCNN)
a.输入：多视图表示

 

 我们使用两种相机配置获得同一3D目标的多个视图。
      （1）我们假设输入形状是沿着某一坐标轴方向垂直的。在这种情况下，我们通过均匀分布在物体周围的12个虚拟相机（每台相隔30度）创建12个渲染视图。
      （2）忽略上边沿坐标轴连续垂直的假设，在这种情况下，我们需要创建更多的视图，因为我们不知道哪个视图更能代表中心目标。所有视图分别由围绕在目标周围的20个虚拟相机生成，每个虚拟相机生成4张视图，方法是将视图围绕坐标轴分别旋转0，90，180，270，最后生成80张视图。
b.基于多视图表示的物体识别
图片描述
        我们利用多尺度SIFT法生成的Fisher向量支持的图片描述方法和CNN激活特征法。两种方法表征图片都取得了不错的性能。得到图像的特征表示后，可以进行目标分类和检索等任务。
4、Multi-View CNN：学习聚合视图
        3D形状的多个视图中的每一张图像都经过网络的第一部分CNN1单独处理，在视图池化层进行聚合后，将结果送入CNN2模块。网络第一部分的所有分支都共享相同的CNN1参数。在视图池化层中，我们在视图间使用元素最大值操作。
点评：
        基于多视图的网络拥有比体素模型更好的性能，主要原因有两方面：首先，它们利用的是早已被详细研究过的2D技术；其次，由于不需要体素量化，因此包含了更丰富的上下文信息。
五、直接在原始点云上应用深度学习方法
       自从2017年PointNet的问世，处理原始点云的深度学习模型就备受关注，尽管点云本身存在诸多挑战，但依然有大量模型发展了起来。卷积神经网络的成功源于卷积操作，随着网络深度的增加，逐级对局部区域进行学习。但是卷积操作要求的结构化网格数据是点云本身不具备的，PointNet究竟用了什么方法，使得它可以直接在点云上应用深度学习方法？现在我们回顾一下PointNet网络。
1.PointNet
       我们用P = R(N × D)表示输入PointNet的点云，其中N点云中点的数量，D是每个点的维度，通常D ＝ 3，代表每个点的XYZ坐标，当然还可以有其他特征。由于点是无序的，因此PointNet是由对称函数组成的。对称函数的特点是，无论输入的顺序如何，输出都相同。PointNet由两个对称函数组成，如下图所示：

 其中一部分是多层感知机，另一部分则是最大池化函数。多层感知机将每个点的特征维度从3维拉伸到了1024维，且每层的点共享所有参数。为了得到1024维的全局特征向量，我们用最大池化对称函数处理MLP的输出结果，得到的全局特征向量可以用于实例分割和目标分类等任务。
       虽然PointNet在许多数据集上都取得了不错的成果，但它并不考虑点之间的局部依赖，因此无法捕捉到局部特征，因此许多后续的方法对PointNet做了适当的改进，使其可以像逐层进行卷积操作一样，捕捉局部区域特征。考虑到点云的无序性，实现这一目标主要分三个基础操作：采样、分组和非线性映射。

 采样：采样主要是为了降低各层中点的分辨率。给定一个包含N个点的点云P ＝ R(N × 3)，采样过程将这个点集规模缩小到了M个点：P' = R(M × 3)，其中M <= N。这M个采样点被称为代表点或者中心点，用以代表对应的被采样的局部区域。有两种采样方法比较受欢迎：随机采样法和最远点采样法。牵着可以使N个点以相同的概率被采样，后者采样的M个点，每个点距离其余M－1个点都是最远的。
分组：基于这些具有代表性的采样点，我们用K近邻算法筛选出与每个代表点最临近的一些临近点，从而组成一个局部的分块，该过程如下图所示：

 这些局部分块中的点将被用来计算这些邻近点的局部特征表示。kNN算法是将每个中心点最近邻的k个邻近点计算出来，除此之外，还可以应用球状查询法，将中心点某个半径内的点筛选出来。
非线性映射函数：一旦每个中心点的邻近点获得之后，下一步就是将他们映射成一个个特征向量，用以表征以该中心点为中心的局部结构。在网格卷积中，通过矩阵和卷积核的相乘和相加操作，感受野被映射到一个特征神经元中。但由于点云的非结构化特征，导致直接在点云上使用这一过程并不容易，因此很多方法使用近似于PointNet的函数，如下：

模型举例：
(1)不考虑点之间关系的
PointNet回顾：给定一个无序的点集{x1，x2，...，xn}，其中xi ∈ Rd，我们可以定义一个函数f：X → R，该函数将一系列的点映射成一个特征向量：

 其中γ和h都是MLP网络。函数f对输入点序列具有不变性，其中h的返回值可以解释为每个点的空间编码。以上是PointNet的基本思想，但PointNet缺乏对点云局部特征的提取能力，PointNet++对此进行了适当的改进。
PointNet++：如下图所示

 这是由一系列set abstraction模块组成的层次结构，每个模块都处理一系列的点并对他们进行抽象，生成一个规模更小的点集。set abstraction模块由三个层组成，分别是采样层、分组层和PointNet层。
      一个set abstraction模块以一个大小为N × (d + C)的矩阵作为输入，其中N是点云中点的数量，每个点拥有d维坐标和C维点特征。它的输出是一个大小为N' × (d + C')的矩阵，其中N'是采样点的数量，d是坐标维度，C'是以采样点为中心的局部邻域的特征向量维度。
Samling layer：给定一个输入点集{x1，x2，...，xn}，我们用最远点采样法（FPS）对其进行采样，
得到子集{xi1，xi2，...，xim}，其中xij相比于剩下的点，和集合{xi1，xi2，...，xij-1}拥有最远的距离。相比于随机采样法，FPS对于同一个中心点对整个点云的覆盖性更强。
Grouping layer：该层的输入是大小为N × (d + C)的原始点云以及大小是N' × d的中心点坐标。该层的输出是大小为N' × K × (d ＋ C)的点集。其中K是以每个采样点为中心的邻域中邻接点的个数，每个邻域的K值可以不同，PointNet有能力将点数量不同的邻域转化为固定大小的局部特征向量。
       球状查询算法作为一种邻接点查询算法，查询以query point为中心的某个半径内的所有点。而kNN算法则是查找固定数量的邻接点。相比于kNN算法，球状查询算法保证查询在一个固定尺度的区域内，因此可以保证局部区域在整个空间内有更强的泛化能力。
PointNet layer：该层的输入是N'个局部区域，每个区域由K个点组成，数据大小为N' × K × (d + C)。输出是每个中心点所对应的局部区域的特征，输出数据的大小是N' × (d + C')。
        局部区域中的点的坐标首先要转换成相对于中心点的相对坐标，即：

 通过运用相对坐标，我们可以捕捉到邻接点和中心点之间的关系。
针对点云密度不均匀情况下的采样，如何提取鲁棒特征？
       如前所述，点云的密度在不同区域有所不同，这种不均匀性对特征学习会带来挑战。比如说，在稠密区域学习到的特征无法泛化到稀疏采样的区域。因此在稀疏点云上训练的模型无法识别细粒度的局部结构。为了克服这一点，PointNet++提出了两种特征融合策略，用于解决当点云局部采样密度改变时，将不同尺度区域的特征结合起来。

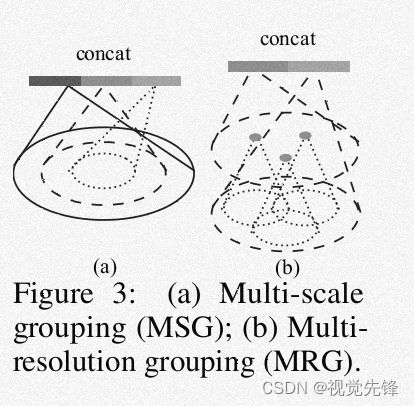
 Multi-scale grouping（MSG）：
       一种最直接的捕获多尺度特征的方式就是在不同尺度的点云上应用grouping layers，然后利用PointNet提取不同尺度的特征，最后将这些特征连接在一起，形成多尺度特征向量。但是MSG方法计算量很大，因为要在不同中心点的邻域上利用PointNet提取特征，尤其在比较低的网络层次上，邻域的尺度会很大，这对节省计算时间和资源都很不利。
Multi-resolution rouping（MRG）：
       层次Li上的区域特征由两部分向量连接而成，左边的向量是对层次较低的Li－1层中每个子区域利用set abstraction模块进行特征提取得到的，右边的向量是通过在整个原始点云上运用PointNet得到的。
       当局部区域的点密度比较低的时候，第一部分向量的可靠性要低于第二部分，因为在生成第一部分向量的时候，各子区域点的稀疏性导致采样效率低下。在这种情况下，第二部分向量会被赋予更高的权值。另一方面，当局部区域的点密度较高的时候，第一部分向量可以提供更丰富的细节信息，因为它会在较低层次上递归探索高分辨率部分。
(2）考虑点之间关系的
点云分析的核心是针对无序的点，发现其潜在的形状特征并加以分辨，能够完成此类任务的模型中，Relation-Shape Convolution（RS－Conv）是比较有代表性的。

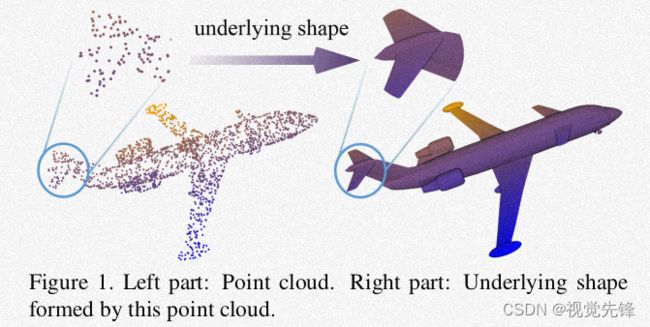
 建模：我们用Psub ⊂ R3将局部点云建模成一个球形邻域，该邻域以采样点xi为中心，其周围的点作为它的相邻点，表示为xj ∈ N（xi）。如下图中左侧部分所示：

 我们的目标是学习特征fPsub，该特征包含潜在的形状信息。我们用一个常规的卷积操作定义该特征如下：

 其中x是3D点，f是一个特征向量。dij是点xi和xj之间的欧式距离，r是球体的半径。在这里我们通过函数T将N（xi）内的所有点的特征进行提取，然后通过带有非线性激活函数的函数A将所有点的特征聚合，得到fPsub。当A是对称函数且N（xi）中所有点共享T中的参数时，模型可以达到对点的序列的不变性。
传统CNN的局限：在传统CNN当中，T是这样运算的：

 

  其中wj是学习到的权重，“.”是元素相乘操作。这样做有两方面局限：
a.wj并非被N（xi）中所有点共享的，导致无法产生对点序列的不变性并且无法处理不规则的点集Psub。
b.wj反向传播的梯度只和单独的一个点xj相关，这就导致学习过程中不会对形状信息有太多感知。
转变（学习点和点之间的关系）：在3D邻域空间中，点xi和其邻近点的几何关系正是空间点布局的一种表示，可以更有分辨性的反应点云中潜在的形状。为了捕捉这种关系，我们把CNN中的wj替换成wij，它由关系向量hij经过M映射得到。我们称hij为较低水平的关系。该过程可以被描述为：

 

 M的目标是抽象出两个点之间高水平的关系表示，以编码点和点的空间布局。M也是基于MLP实现的，具体过程如图中间所示。此时wij的反向传播梯度和点xi以及点xj有关，同时，M的参数被N（xi）中的所有点共享，如此我们就可以克服点云的不规则性了。最终，式1可以写成如下形式：

 

(3)基于图的方法

Dynamic Graph CNN（DGCNN）：
       考虑有一个n个点的点云，每个点的特征维度是F，表示为：X＝{x1，x2，...，xn} ⊆ R^F。最简单的设定是F＝3，即每个点包含3D坐标xi＝（xi，yi，zi）；当然也可以包括颜色等其他特征。在深度网络结构中，每个子层的输入都是前一层的输出，因此维度F通常指代给定层特征的维度。
       我们用一个图G＝（V，E）来代表一个局部点云，其中V＝{1，...，n}和E ⊆ V × V分别是图的节点和边。在最简单的情况下，我们用kNN算法生成R^F空间中点云X的图G。该图中包括环路，代表每个节点也可以指向自己。我们定义特征eij＝hθ（xi，xj），其中hθ：R^F × R^F → R^F'是参数为θ的非线性映射函数。
       最后，我们定义边卷积操作。我们针对与每个点相关联的边的特征，使用通道级对称聚合操作（Σ或者max），第i个节点的边卷积输出为：

 从宏观角度看，维度是F的n个点的点云经过边卷积操作就变成了维度是F'的相同大小的点云。

 

  网络结构如下： 

 我们在网络的每一层中都会有一份不同的图G^l＝（V^l，E^l），其中每层的图都可以表示为（i，ji1），...，（i，jkl）。我们的框架在每一层都会学习如何构建图，调整图的结构。在具体实验中，我们会计算一个矩阵，存储每对点的距离，然后针对每个点选取出与它最近邻的k个点。

 各类经典深度学习方法汇总

 数据集：

 评价指标：

 

 参考文献：
Deep Learning for 3D Point Clouds: A Survey
Deep Learning for LiDAR Point Clouds in Autonomous Driving: A Review
Review: deep learning on 3D point clouds
Deep Learning for 3D Point Cloud Understanding: A Survey
Dynamic Graph CNN for Learning on Point Clouds
Learning a Probabilistic Latent Space of Object Shapes via 3D Generative-Adversarial Modeling
PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space
Relation-Shape Convolutional Neural Network for Point Cloud Analysis
Multi-view Convolutional Neural Networks for 3D Shape Recognition