Pytorch ，Conv2D、MaxPool2D和ConvTranspose2d

1.MaxPool2d

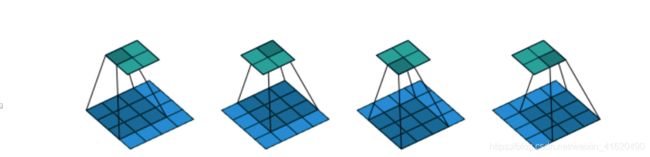
假设现在有一个4×4的图片，以及一个3 ×3的卷积核，在没有padding的情况下，逐列逐行扫描, 即步长，stride = 1。扫描过程如下，就是取每一个核中的最大值

代码实现：
假设batch = 2，channel=1， 即有两个4×4的单色图

x = torch.randn(2,1,4,4)
print(x)

这里即随机的初始化两个 4*4的单色图

tensor([[[[ 1.7259, -0.5743, -1.3798,  0.9360],
			        [-1.7684,  1.6721,  0.5619,  1.7224],
			         [-0.6477,  1.4126,  0.3330,  0.4354],
			         [-0.2691, -1.5763, -0.5866, -0.0692]]],
			
			
			       [[[ 0.0483,  1.1245, -1.3001,  0.7481],
			         [ 0.2676, -1.3854,  0.2261,  2.1940],
			         [-1.8022,  1.8357,  1.7572,  1.1644],
			         [ 1.0082, -0.8614,  0.7588,  0.2475]]]])

对于第一个矩阵，我们可以很容易的得出经过MaxPool2D的矩阵为：
[1.7259, 1.7224
1.6721, 1.7224]

model = torch.nn.MaxPool2d(kernel_size=3,stride=1)
print(model(x))

结果为

tensor([[[[1.7259, 1.7224],
		          [1.6721, 1.7224]]],
		
		
		        [[[1.8357, 2.1940],
		          [1.8357, 2.1940]]]])

2.Conv2d

卷积可以认为是一个特征提取的过程，其过程和MaxPool2d十分相似，只是计算的过程的不一样，

• MaxPool2d的操作是取核中所选范围内矩阵的最大值
• Conv2d的操作则是 矩阵的值和卷积核的值 相乘相加

代码实现：
以 1个4×4的单色图 为例子，即channel = 1，如果是彩图，通道则为RGB三种,即channel = 3
先随机一个图片

x = torch.randn(1,1,4,4)

建立一个卷积操作，注意这里的out_channels表示输出通道，in_channels代表输入通道，输入通道我们之前定义为1, 但是没有对输出通道做出限制。

其实，一个卷积核对应输出一个矩阵，所以在这里就相当于是使用了out_channels个卷积核。下面暂定为3个输出通道

model = torch.nn.Conv2d(in_channels=1, out_channels=3, kernel_size=3,stride=1)
model(x).shape

其结果为

torch.Size([1, 3, 2, 2])

1 代表batch_size, 3表示out_channels，后面的两个2表示生成的矩阵为2×2
相当于提取了原来矩阵的两个特征

3. ConvTranspose2d

ConvTranspose2d和Conv2d在参数一样的情况下，其输入和输出是刚好完全相反的

第二节中，我们把图像降维，可以称其为下采样。

反过来，本节是要升维，把一个2×2 的矩阵，升为4×4的矩阵，称为上采样。

其过程为：

• 先计算出新的矩阵维度(填充后的矩阵）
• 在新的矩阵之上进行一次正常的卷积操作

3.1、例子1

现在我们以第二节中的输出维度为例子

x = torch.randn(1,1,2,2)  # 随机一个batch=1, channel=1,2*2的图像
mo = nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=3, stride=1)
mo(x).shape

其结果为

torch.Size([1, 1, 4, 4])

这里先把矩阵填充为６* 6，然后再用卷积核进行正常的卷积操作
图片链接

其实这里自动添加了两层的padding，但是参数也要设置padding=0

例子２

和上述的参数一直，但是设置stride＝２

x = torch.randn(1,1,2,2)
mo = nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=3, stride=2)
mo(x).shape

结果为

torch.Size([1, 1, 5,5])

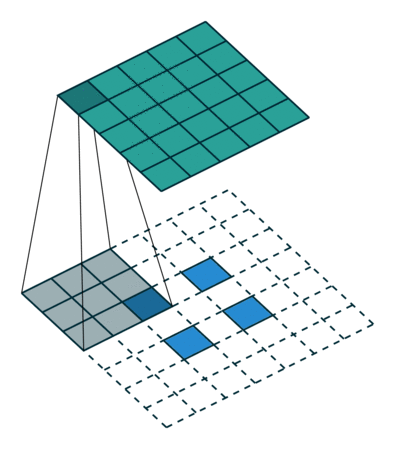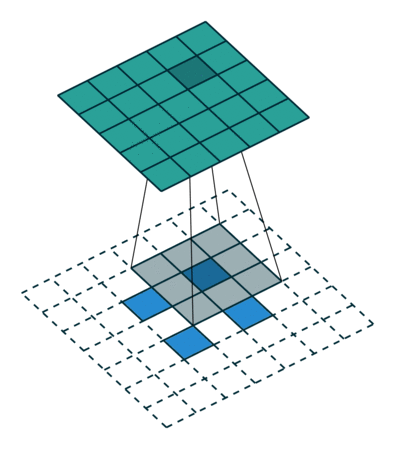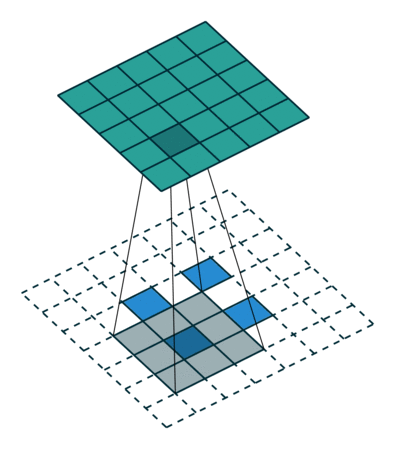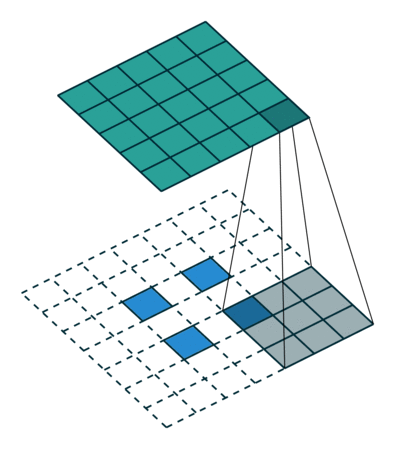
这里先把原本的矩阵按照stride=2分开，然后再用卷即核一步一步进行计算

3.2、torch 参数含义

ConvTranspose2d 和Conv2d是完全相反的。以下面这个例子为例子

代码为

x = torch.randn(1,1,2,2)
conv_trans = (nn.ConvTranspose2d(in_channels=3, out_channels=3, kernel_size=3, stride=1, padding=0))
conv_trans(x).shape

蓝色到绿色块
这里我们的输入是蓝色的2 × 2的块，输出的绿颜色的4 ×4的块。我们可以通过如下公式计算 从 蓝色到绿色 的过程, 这个公式是卷积的过程，因此output = 2是蓝色块，input是绿色块
$$\frac{input+2p-k}{s}+1=ouput$$
我们就可以求得绿色块 input = 4.。 其实就是上述API得出的值

绿色块 到白色块，这里s=1
$$\frac{蓝色+2p^{\prime }-k}{s}+1=绿色$$
我们可以求得p'=2，所以下面白色块大小为2 + 2×2 = 6