acm拿国奖的第三关：链表

目录

一，单链表

1，单链表的实现

2，增加操作

3，删除操作

二，链表中的双指针技巧

例题1：环形链表

复杂度分析

双指针模板：

提示

复杂度分析

三，经典问题--反转链表

例题1：反转链表

复杂度分析

经验之谈：

1. 通过一些测试用例可以节省您的时间。

2. 你可以同时使用多个指针。

3. 在许多情况下，你需要跟踪当前结点的前一个结点。

四，双链表

定义

1，双链表实现

2，增加操作

3，删除操作

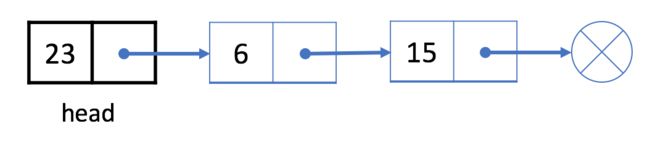
与数组相似，链表也是一种线性数据结构。这里有一个例子：

正如你所看到的，链表中的每个元素实际上是一个单独的对象，而所有对象都通过每个元素中的引用字段链接在一起。

链表有两种类型：单链表和双链表。上面给出的例子是一个单链表，这里有一个双链表的例子：

一，单链表

单链表中的每个结点不仅包含值，还包含链接到下一个结点的引用字段。通过这种方式，单链表将所有结点按顺序组织起来。

下面是一个单链表的例子：

1，单链表的实现

// Definition for singly-linked list.
struct SinglyListNode {
    int val;//数据域
    SinglyListNode *next;//指针域
    SinglyListNode(int x) : val(x), next(NULL) {}
};

与数组不同，我们无法在常量时间内访问单链表中的随机元素。 如果我们想要获得第 i 个元素，我们必须从头结点逐个遍历。 我们按索引来访问元素平均要花费 O(N) 时间，其中 N 是链表的长度。

例如，在上面的示例中，头结点是 23。访问第 3 个结点的唯一方法是使用头结点中的“next”字段到达第 2 个结点（结点 6）; 然后使用结点 6 的“next”字段，我们能够访问第 3 个结点。

你可能想知道为什么链表很有用，尽管它在通过索引访问数据时（与数组相比）具有如此糟糕的性能。 在接下来的文章中，我们将介绍插入和删除操作，你将了解到链表的好处。

2，增加操作

如果我们想在给定的结点 prev 之后添加新值，我们应该：

使用给定值初始化新结点 cur；

将 cur 的 next 字段链接到 prev 的下一个结点 next ；

将 prev 中的 next 字段链接到 cur 。

与数组不同，我们不需要将所有元素移动到插入元素之后。因此，您可以在 O(1) 时间复杂度中将新结点插入到链表中，这非常高效。

在开头添加结点
众所周知，我们使用头结点来代表整个列表。

因此，在列表开头添加新节点时更新头结点 head 至关重要。

初始化一个新结点 cur ；
将新结点链接到我们的原始头结点 head。
将 cur 指定为 head 。
例如，让我们在列表的开头添加一个新结点 9 。

我们初始化一个新结点 9 并将其链接到当前头结点 23 。

指定结点 9 为新的头结点。

如何在列表的末尾添加新的结点？我们还能使用类似的策略吗？

3，删除操作

如果我们想从单链表中删除现有结点 cur，可以分两步完成：

找到 cur 的上一个结点 prev 及其下一个结点 next ；

接下来链接 prev 到 cur 的下一个节点 next 。

在我们的第一步中，我们需要找出 prev 和 next。使用 cur 的参考字段很容易找出 next，但是，我们必须从头结点遍历链表，以找出 prev，它的平均时间是 O(N)，其中 N 是链表的长度。因此，删除结点的时间复杂度将是 O(N)。

空间复杂度为 O(1)，因为我们只需要常量空间来存储指针

删除第一个结点
如果我们想删除第一个结点，策略会有所不同。

正如之前所提到的，我们使用头结点 head 来表示链表。我们的头是下面示例中的黑色结点 23。

如果想要删除第一个结点，我们可以简单地将下一个结点分配给 head。也就是说，删除之后我们的头将会是结点 6。

链表从头结点开始，因此结点 23 不再在我们的链表中。

删除最后一个结点呢？我们还能使用类似的策略吗？

二，链表中的双指针技巧

让我们从一个经典问题开始：

给定一个链表，判断链表中是否有环。

你可能已经使用哈希表提出了解决方案。但是，使用双指针技巧有一个更有效的解决方案。在阅读接下来的内容之前，试着自己仔细考虑一下。

想象一下，有两个速度不同的跑步者。如果他们在直路上行驶，快跑者将首先到达目的地。但是，如果它们在圆形跑道上跑步，那么快跑者如果继续跑步就会追上慢跑者。

这正是我们在链表中使用两个速度不同的指针时会遇到的情况：

如果没有环，快指针将停在链表的末尾。
如果有环，快指针最终将与慢指针相遇。
所以剩下的问题是：

这两个指针的适当速度应该是多少？

一个安全的选择是每次移动慢指针一步，而移动快指针两步。每一次迭代，快速指针将额外移动一步。如果环的长度为 M，经过 M 次迭代后，快指针肯定会多绕环一周，并赶上慢指针。

那其他选择呢？它们有用吗？它们会更高效吗？

例题1：环形链表

141. 环形链表 - 力扣（LeetCode）https://leetcode.cn/problems/linked-list-cycle/

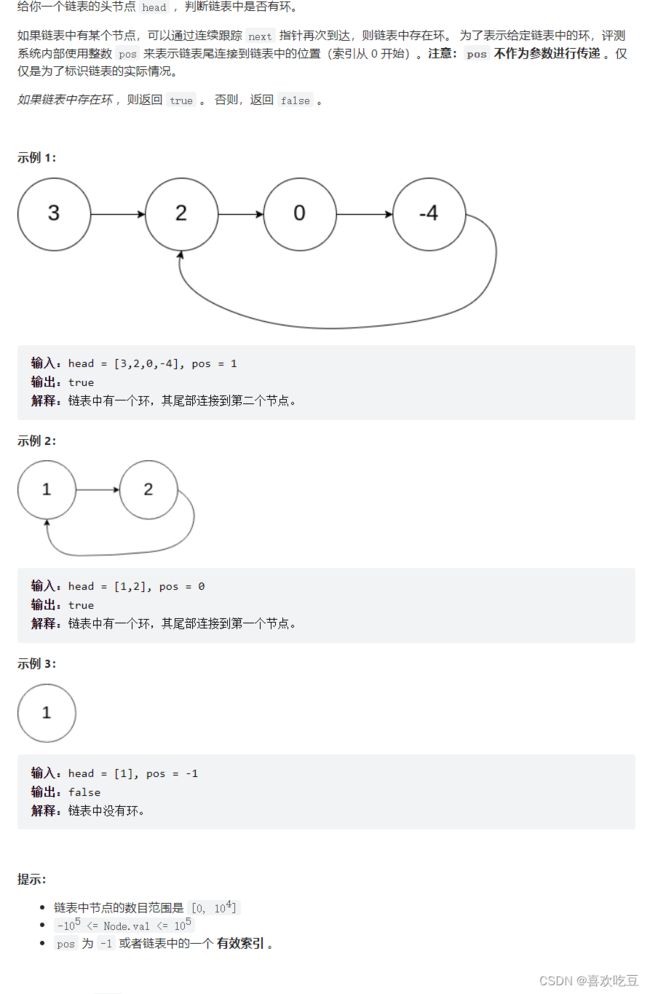
本方法需要读者对「Floyd 判圈算法」（又称龟兔赛跑算法）有所了解。

假想「乌龟」和「兔子」在链表上移动，「兔子」跑得快，「乌龟」跑得慢。当「乌龟」和「兔子」从链表上的同一个节点开始移动时，如果该链表中没有环，那么「兔子」将一直处于「乌龟」的前方；如果该链表中有环，那么「兔子」会先于「乌龟」进入环，并且一直在环内移动。等到「乌龟」进入环时，由于「兔子」的速度快，它一定会在某个时刻与乌龟相遇，即套了「乌龟」若干圈。

我们可以根据上述思路来解决本题。具体地，我们定义两个指针，一快一慢。慢指针每次只移动一步，而快指针每次移动两步。初始时，慢指针在位置 head，而快指针在位置 head.next。这样一来，如果在移动的过程中，快指针反过来追上慢指针，就说明该链表为环形链表。否则快指针将到达链表尾部，该链表不为环形链表。

细节

为什么我们要规定初始时慢指针在位置 head，快指针在位置 head.next，而不是两个指针都在位置 head（即与「乌龟」和「兔子」中的叙述相同）？

观察下面的代码，我们使用的是 while 循环，循环条件先于循环体。由于循环条件一定是判断快慢指针是否重合，如果我们将两个指针初始都置于 head，那么 while 循环就不会执行。因此，我们可以假想一个在 head 之前的虚拟节点，慢指针从虚拟节点移动一步到达 head，快指针从虚拟节点移动两步到达 head.next，这样我们就可以使用 while 循环了。

当然，我们也可以使用 do-while 循环。此时，我们就可以把快慢指针的初始值都置为 head。

class Solution {
public:
    bool hasCycle(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return false;
        }
        ListNode* slow = head;
        ListNode* fast = head->next;
        while (slow != fast) {
            if (fast == nullptr || fast->next == nullptr) {
                return false;
            }
            slow = slow->next;
            fast = fast->next->next;
        }
        return true;
    }
};

复杂度分析

时间复杂度：O(N)，其中 NN 是链表中的节点数。

当链表中不存在环时，快指针将先于慢指针到达链表尾部，链表中每个节点至多被访问两次。

当链表中存在环时，每一轮移动后，快慢指针的距离将减小一。而初始距离为环的长度，因此至多移动 N 轮。

空间复杂度：O(1)。我们只使用了两个指针的额外空间。

双指针模板：

// Initialize slow & fast pointers
ListNode* slow = head;
ListNode* fast = head;
/**
 * Change this condition to fit specific problem.
 * Attention: remember to avoid null-pointer error
 **/
while (slow && fast && fast->next) {
    slow = slow->next;          // move slow pointer one step each time
    fast = fast->next->next;    // move fast pointer two steps each time
    if (slow == fast) {         // change this condition to fit specific problem
        return true;
    }
}
return false;   // change return value to fit specific problem

提示

它与我们在数组中学到的内容类似。但它可能更棘手而且更容易出错。你应该注意以下几点：

1. 在调用 next 字段之前，始终检查节点是否为空。

获取空节点的下一个节点将导致空指针错误。例如，在我们运行 fast = fast.next.next 之前，需要检查 fast 和 fast.next 不为空。

2. 仔细定义循环的结束条件。

运行几个示例，以确保你的结束条件不会导致无限循环。在定义结束条件时，你必须考虑我们的第一点提示。

复杂度分析

空间复杂度分析容易。如果只使用指针，而不使用任何其他额外的空间，那么空间复杂度将是 O(1)。但是，时间复杂度的分析比较困难。为了得到答案，我们需要分析运行循环的次数。

在前面的查找循环示例中，假设我们每次移动较快的指针 2 步，每次移动较慢的指针 1 步。

如果没有循环，快指针需要 N/2 次才能到达链表的末尾，其中 N 是链表的长度。
如果存在循环，则快指针需要 M 次才能赶上慢指针，其中 M 是列表中循环的长度。
显然，M <= N 。所以我们将循环运行 N 次。对于每次循环，我们只需要常量级的时间。因此，该算法的时间复杂度总共为 O(N)。

自己分析其他问题以提高分析能力。别忘了考虑不同的条件。如果很难对所有情况进行分析，请考虑最糟糕的情况。

三，经典问题--反转链表

让我们从一个经典问题开始：

反转一个单链表。

一种解决方案是按原始顺序迭代结点，并将它们逐个移动到列表的头部。似乎很难理解。我们先用一个例子来说明我们的算法。

例题1：反转链表

206. 反转链表 - 力扣（LeetCode）https://leetcode.cn/problems/reverse-linked-list/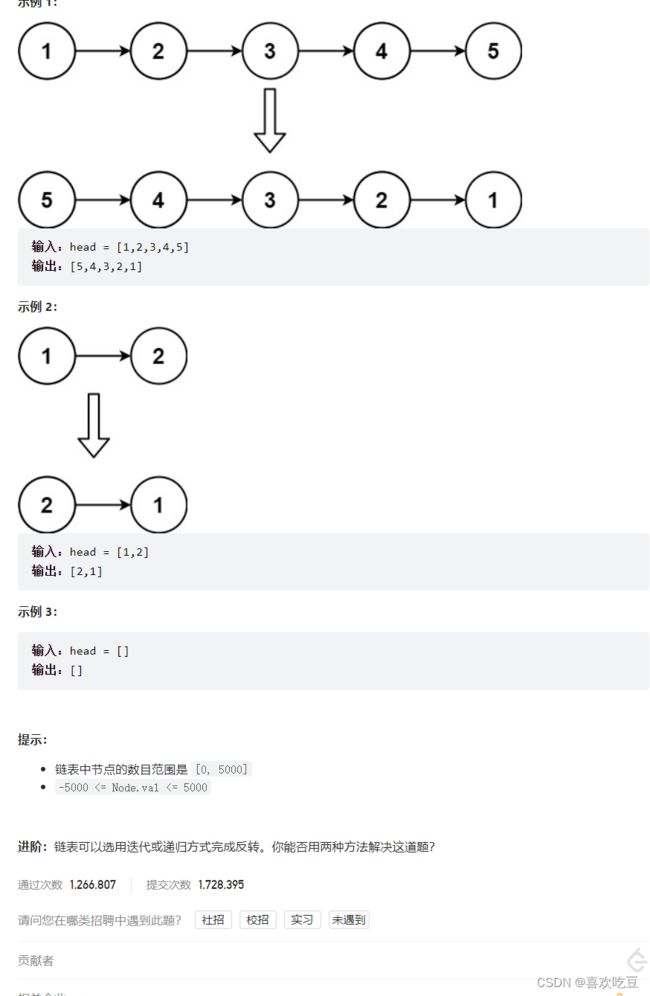

 

假设链表为 1→2→3→∅，我们想要把它改成∅←1←2←3。

在遍历链表时，将当前节点的 next 指针改为指向前一个节点。由于节点没有引用其前一个节点，因此必须事先存储其前一个节点。在更改引用之前，还需要存储后一个节点。最后返回新的头引用。

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* prev = nullptr;
        ListNode* curr = head;
        while (curr) {
            ListNode* next = curr->next;
            curr->next = prev;
            prev = curr;
            curr = next;
        }
        return prev;
    }
};

复杂度分析

• 时间复杂度：O(n)，其中 n 是链表的长度。需要遍历链表一次。

• 空间复杂度：O(1)。

经验之谈：

1. 通过一些测试用例可以节省您的时间。

使用链表时不易调试。因此，在编写代码之前，自己尝试几个不同的示例来验证您的算法总是很有用的。

2. 你可以同时使用多个指针。

有时，当你为链表问题设计算法时，可能需要同时跟踪多个结点。您应该记住需要跟踪哪些结点，并且可以自由地使用几个不同的结点指针来同时跟踪这些结点。

如果你使用多个指针，最好为它们指定适当的名称，以防将来必须调试或检查代码。

3. 在许多情况下，你需要跟踪当前结点的前一个结点。

你无法追溯单链表中的前一个结点。因此，您不仅要存储当前结点，还要存储前一个结点。这在双链表中是不同的。

四，双链表

定义

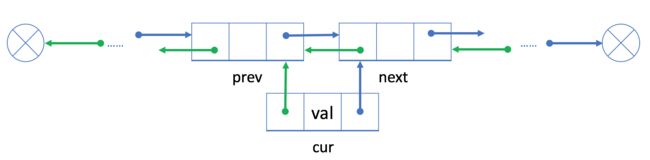
双链表以类似的方式工作，但还有一个引用字段，称为“prev”字段。有了这个额外的字段，您就能够知道当前结点的前一个结点。

让我们看一个例子：

绿色箭头表示我们的“prev”字段是如何工作的。

1，双链表实现

// Definition for doubly-linked list.
struct DoublyListNode {
    int val;
    DoublyListNode *next, *prev;
    DoublyListNode(int x) : val(x), next(NULL), prev(NULL) {}
};

2，增加操作

如果我们想在现有的结点 prev 之后插入一个新的结点 cur，我们可以将此过程分为两个步骤：

链接 cur 与 prev 和 next，其中 next 是 prev 原始的下一个节点；

用 cur 重新链接 prev 和 next。

与单链表类似，添加操作的时间和空间复杂度都是 O(1)。

3，删除操作

如果我们想从双链表中删除一个现有的结点 cur，我们可以简单地将它的前一个结点 prev 与下一个结点 next 链接起来。

与单链表不同，使用“prev”字段可以很容易地在常量时间内获得前一个结点。

因为我们不再需要遍历链表来获取前一个结点，所以时间和空间复杂度都是O(1)。