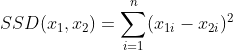NNDL 实验七 循环神经网络（2）梯度爆炸实验

目录

6.2 梯度爆炸实验

6.2.1 梯度打印函数

6.2.2 复现梯度爆炸现象

 6.2.3 使用梯度截断解决梯度爆炸问题

【思考题】梯度截断解决梯度爆炸问题的原理是什么？

---

6.2 梯度爆炸实验

造成简单循环网络较难建模长程依赖问题的原因有两个：梯度爆炸和梯度消失。

梯度爆炸问题：比较容易解决，一般通过权重衰减或梯度截断可以较好地来避免；

梯度消失问题：更加有效的方式是改变模型，比如通过长短期记忆网络LSTM来进行缓解。

---

本节将首先进行复现简单循环网络中的梯度爆炸问题，然后尝试使用梯度截断的方式进行解决。

采用长度为20的数据集进行实验，

训练过程中将进行输出W,U,b的梯度向量的范数，以此来衡量梯度的变化情况。

6.2.1 梯度打印函数

在训练过程中打印梯度

使用custom_print_log实现了在训练过程中打印梯度的功能，custom_print_log需要接收runner的实例，并通过model.named_parameters()获取该模型中的参数名和参数值. 这里我们分别定义W_list, U_list和b_list，用于分别存储训练过程中参数W,U和b的梯度范数。

import torch

W_list = []
U_list = []
b_list = []


# 计算梯度范数
def custom_print_log(runner):
    model = runner.model
    W_grad_l2, U_grad_l2, b_grad_l2 = 0, 0, 0
    for name, param in model.named_parameters():
        if name == "rnn_model.W":
            W_grad_l2 = torch.norm(param.grad, p=2).numpy()
        if name == "rnn_model.U":
            U_grad_l2 = torch.norm(param.grad, p=2).numpy()
        if name == "rnn_model.b":
            b_grad_l2 = torch.norm(param.grad, p=2).numpy()
    print(f"[Training] W_grad_l2: {W_grad_l2:.5f}, U_grad_l2: {U_grad_l2:.5f}, b_grad_l2: {b_grad_l2:.5f} ")
    W_list.append(W_grad_l2)
    U_list.append(U_grad_l2)
    b_list.append(b_grad_l2)

【思考】什么是范数，什么是L2范数，这里为什么要打印梯度范数？

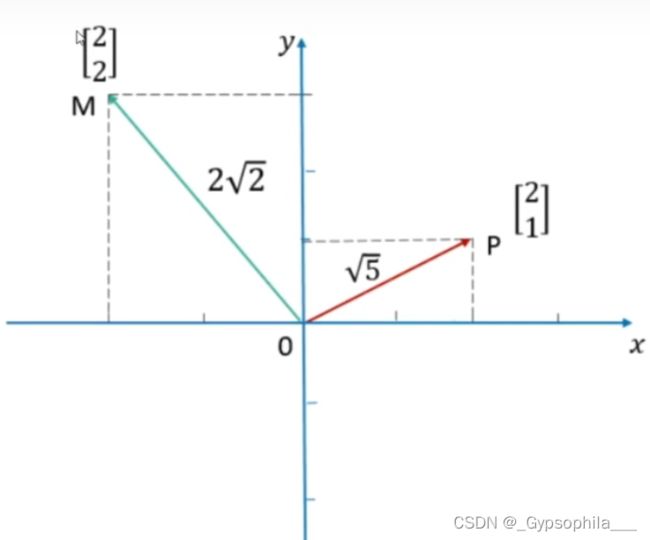
范数

我们知道距离的定义是一个宽泛的概念，只要满足非负、自反、三角不等式就可以称之为距离。范数是一种强化了的距离概念，它在定义上比距离多了一条数乘的运算法则。有时候为了便于理解，我们可以把范数当作距离来理解。

在数学上，范数包括向量范数和矩阵范数，向量范数表征向量空间中向量的大小，矩阵范数表征矩阵引起变化的大小。一种非严密的解释就是，对应向量范数，向量空间中的向量都是有大小的，这个大小如何度量，就是用范数来度量的，不同的范数都可以来度量这个大小，就好比米和尺都可以来度量远近一样；对于矩阵范数，学过线性代数，我们知道，通过运算AX=B，可以将向量X变化为B，矩阵范数就是来度量这个变化大小的。

范数定义了向量空间里的距离，它的出现使得向量之间的比较成为了可能。

简单理解：范数可以把一组实数列表，映射成一个实数。

范数是一个函数，表示方式为||x||,

L2范数

L2范数是我们最常见最常用的范数了，我们用的最多的度量距离欧氏距离就是一种L2范数，它的定义如下：

  表示向量元素的平方和再开平方。

L2也可以度量两个向量间的差异，如平方差和

 对于L2范数，它的优化问题如下：

L2范数通常会被用来做优化目标函数的正则化项，防止模型为了迎合训练集而过于复杂造成过拟合的情况，从而提高模型的泛化能力。

为什么要打印梯度范数:函数在某一点处的方向导数在其梯度方向上达到最大值,此最大值即梯度的范数。 而模型的学习过程是通过使用训练数据来最小化损失函数，从而确定参数的值。而最小化损失函数，即通过求导求损失函数的极值。打印梯度范数值可以帮助我们更直观地了解模型训练情况的好坏，梯度过大或过小都有可能导致模型的训练效果变差，因此打印梯度范数有利于我们更快地对模型作出修改。

6.2.2 复现梯度爆炸现象

为了更好地复现梯度爆炸问题，使用SGD优化器将批大小和学习率调大，学习率为0.2，同时在计算交叉熵损失时，将reduction设置为sum，表示将损失进行累加。 

import os
import random
import torch
import numpy as np
 
np.random.seed(0)
random.seed(0)
torch.manual_seed(0)
 
# 训练轮次
num_epochs = 50
# 学习率
lr = 0.2
# 输入数字的类别数
num_digits = 10
# 将数字映射为向量的维度
input_size = 32
# 隐状态向量的维度
hidden_size = 32
# 预测数字的类别数
num_classes = 19
# 批大小
batch_size = 64
# 模型保存目录
save_dir = "./checkpoints"
 
 
# 可以设置不同的length进行不同长度数据的预测实验
length = 20
print(f"\n====> Training SRN with data of length {length}.")
 
# 加载长度为length的数据
data_path = f"D:/datasets/{length}"
train_examples, dev_examples, test_examples = load_data(data_path)
train_set, dev_set, test_set = DigitSumDataset(train_examples), DigitSumDataset(dev_examples),DigitSumDataset(test_examples)
train_loader = torch.utils.data.DataLoader(train_set, batch_size=batch_size)
dev_loader = torch.utils.data.DataLoader(dev_set, batch_size=batch_size)
test_loader = torch.utils.data.DataLoader(test_set, batch_size=batch_size)
# 实例化模型
base_model = SRN(input_size, hidden_size)
model = Model_RNN4SeqClass(base_model, num_digits, input_size, hidden_size, num_classes)
# 指定优化器
optimizer = torch.optim.SGD(model.parameters(),lr)
# 定义评价指标
metric = Accuracy()
# 定义损失函数
loss_fn = nn.CrossEntropyLoss(reduction="sum")
 
# 基于以上组件，实例化Runner
runner = RunnerV3(model, optimizer, loss_fn, metric)
 
# 进行模型训练
model_save_path = os.path.join(save_dir, f"srn_explosion_model_{length}.pdparams")
runner.train(train_loader, dev_loader, num_epochs=num_epochs, eval_steps=100, log_steps=1,
             save_path=model_save_path, custom_print_log=custom_print_log)

 

获取训练过程中关于W，U和b参数梯度的L2范数，并将其绘制为图片以便展示。

import matplotlib.pyplot as plt
def plot_grad(W_list, U_list, b_list, save_path, keep_steps=40):
    # 开始绘制图片
    plt.figure()
    # 默认保留前40步的结果
    steps = list(range(keep_steps))
    plt.plot(steps, W_list[:keep_steps], "r-", color="#e4007f", label="W_grad_l2")
    plt.plot(steps, U_list[:keep_steps], "-.", color="#f19ec2", label="U_grad_l2")
    plt.plot(steps, b_list[:keep_steps], "--", color="#000000", label="b_grad_l2")
 
    plt.xlabel("step")
    plt.ylabel("L2 Norm")
    plt.legend(loc="upper right")
    plt.show()
    plt.savefig(save_path)
    print("image has been saved to: ", save_path)
 
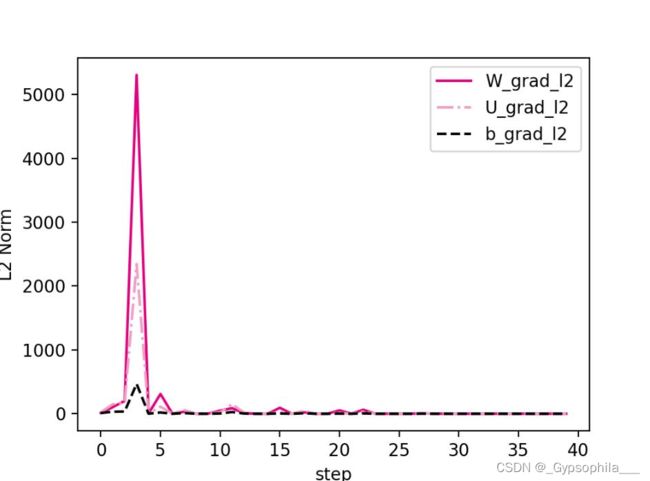
save_path = f"./images/6.8.pdf"
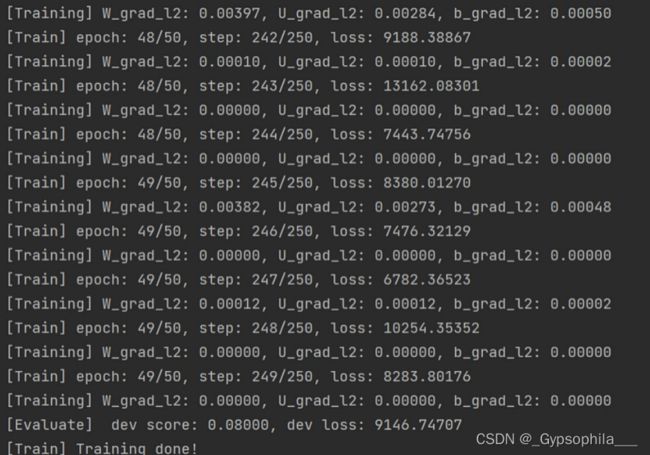
plot_grad(W_list, U_list, b_list, save_path)

 

在训练过程中关于W，U和b参数梯度的L2范数，可以看到经过学习率等方式的调整，梯度范数急剧变大，而后梯度范数几乎为0. 这是因为TanhTanh为SigmoidSigmoid型函数，其饱和区的导数接近于0，由于梯度的急剧变化，参数数值变的较大或较小，容易落入梯度饱和区，导致梯度为0，模型很难继续训练.

 接下来，使用该模型在测试集上进行测试。

print(f"Evaluate SRN with data length {length}.")
# 加载训练过程中效果最好的模型
model_path = os.path.join(save_dir, "srn_explosion_model_20.pdparams")
torch.load(model_path)
 
# 使用测试集评价模型，获取测试集上的预测准确率
score, _ = runner.evaluate(test_loader)
print(f"[SRN] length:{length}, Score: {score: .5f}")

 6.2.3 使用梯度截断解决梯度爆炸问题

梯度截断是一种可以有效解决梯度爆炸问题的启发式方法，

当梯度的模大于一定阈值时，就将它截断成为一个较小的数。

一般有两种截断方式：按值截断和按模截断．

本实验使用按模截断的方式解决梯度爆炸问题。

按模截断是按照梯度向量g的模进行截断，保证梯度向量的模值不大于阈值b，裁剪后的梯度为:

                             

 当梯度向量g的模不大于阈值b时，g数值不变，否则对g进行数值缩放。

在飞桨中，可以使用paddle.nn.ClipGradByNorm进行按模截断.--- pytorch中用什么？

nn.utils.clip_grad_norm_(parameters=model.parameters(), max_norm=20, norm_type=2)

在引入梯度截断之后，将重新观察模型的训练情况。这里我们重新实例化一下：模型和优化器，然后组装runner，进行训练。代码实现如下：

# 清空梯度列表
W_list.clear()
U_list.clear()
b_list.clear()
# 实例化模型
base_model = SRN(input_size, hidden_size)
model = Model_RNN4SeqClass(base_model, num_digits, input_size, hidden_size, num_classes)
 
# 定义clip，并实例化优化器
 
optimizer = torch.optim.SGD(lr=lr, params=model.parameters())
# 定义评价指标
metric = Accuracy()
# 定义损失函数
loss_fn = nn.CrossEntropyLoss(reduction="sum")
 
# 实例化Runner
runner = RunnerV3(model, optimizer, loss_fn, metric)
 
# 训练模型
model_save_path = os.path.join(save_dir, f"srn_fix_explosion_model_{length}.pdparams")
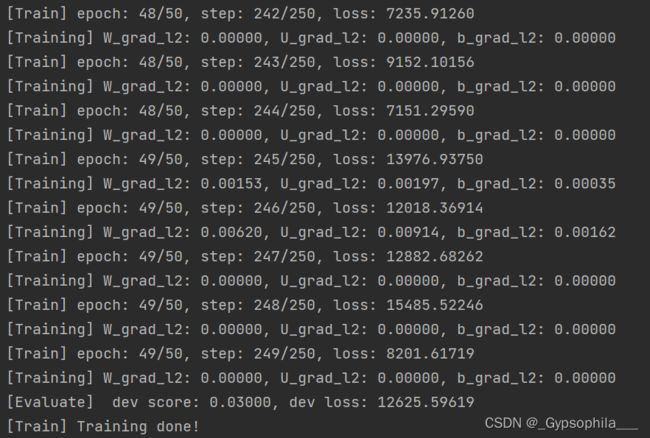
runner.train(train_loader, dev_loader, num_epochs=num_epochs, eval_steps=100, log_steps=1, save_path=model_save_path, custom_print_log=custom_print_log)
# 进行模型训练
model_save_path = os.path.join(save_dir, f"srn_explosion_model_{length}.pdparams")

 在引入梯度截断后，获取训练过程中关于W，U和b参数梯度的L2范数，并将其绘制为图片以便展示，相应代码如下：

save_path = f"./images/6.9.pdf"
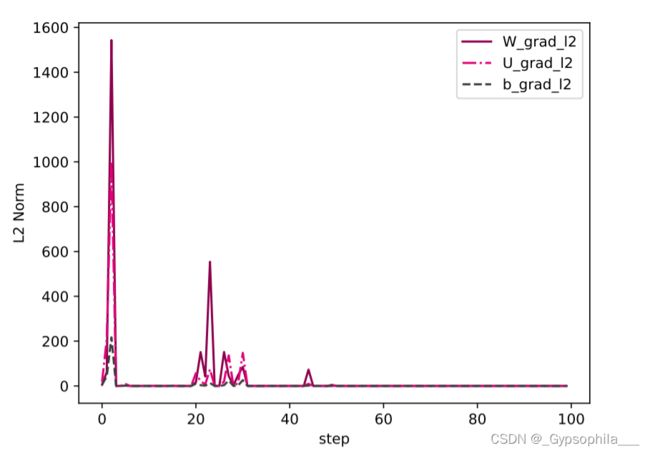
plot_grad(W_list, U_list, b_list, save_path, keep_steps=100)

  展示了引入按模截断的策略之后，模型训练时参数梯度的变化情况。可以看到，随着迭代步骤的进行，梯度始终保持在一个有值的状态，表明按模截断能够很好地解决梯度爆炸的问题.

接下来，使用梯度截断策略的模型在测试集上进行测试。

print(f"Evaluate SRN with data length {length}.")
 
# 加载训练过程中效果最好的模型
model_path = os.path.join(save_dir, f"srn_fix_explosion_model_{length}.pdparams")
runner.load_model(model_path)
 
# 使用测试集评价模型，获取测试集上的预测准确率
score, _ = runner.evaluate(test_loader)
print(f"[SRN] length:{length}, Score: {score: .5f}")

由于为复现梯度爆炸现象，改变了学习率，优化器等，因此准确率相对比较低。但由于采用梯度截断策略后，在后续训练过程中，模型参数能够被更新优化，因此准确率有一定的提升。

【思考题】梯度截断解决梯度爆炸问题的原理是什么？

设定阈值，当预更新的梯度小于阈值时，那么将预更新的梯度设置为阈值

一种是在参数更新之前，逐元素地截断小批量参数梯度。另一种是在参数更新之前截断梯度g的范数||g||：

 其中v是范数上界，g用来更新参数，因为所有参数(包括不同的参数组，如权重和偏置)的梯度被单个缩放因子联合重整化，所以最后一方法具有的优点保证了每个步骤仍是在方向上的，但实验表明两种形式类似。虽然参数更新与真实梯度具有相同的方向梯度，经过梯度范数截断，参数更新的向量范数现在变得有界。这种有界梯度能避免执行梯度爆炸时的有害一步。事实上，当梯度大小高于阈值时，即使采用简单的随机步骤往往工作得几乎一样好。如果爆炸非常严重，梯度数值上为Inf或Nan(无穷大或不是一个数字)，则可以采取大小为v的随机一步，通常会离开数值不稳定的状态。截断每小批量梯度范数不会改变单个小批量的梯度方向。然而，许多小批量使用范数截断后的平均值不等于截断真实梯度(使用所有的实例形成的梯度)的范数。大导数范数的样本，和像这样的出现在同一小批量的样本，其最最终方向的贡献将消失。不像传统小批量梯度下降，其中真实梯度的方向是等于所有小批量梯度的平均。换句话说，传统的随机梯度使用梯度的无偏估计，而与真实梯度或小批量的梯度不再对齐，但是它仍是一个下降方向。

 总结：

本次实验主要是用梯度截断解决梯度爆炸问题，了解了梯度截断解决梯度爆炸问题的原理，在复现简单循环网络中的梯度爆炸问题，再使用梯度截断的方式解决的过程中更深的体会了解梯度爆炸

ref：https://blog.csdn.net/qq_38975453/article/details/126800066

https://zhuanlan.zhihu.com/p/67120415

https://zhuanlan.zhihu.com/p/471333896

https://blog.csdn.net/weixin_36670529/article/details/103937794

NNDL 实验6（上） - HBU_DAVID - 博客园 (cnblogs.com)