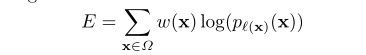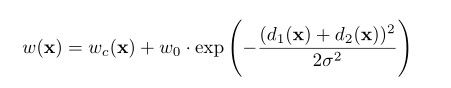论文阅读笔记:《U-Net: Convolutional Networks for Biomedical Image Segmentation》
论文阅读笔记:《U-Net: Convolutional Networks for Biomedical Image Segmentation》
论文下载地址:U-Net
转载请注明:https://blog.csdn.net/weixin_42143615/article/details/108910548
一、论文简介
在本文中,作者提出了一种网络结构和训练策略,它依赖于充分利用数据增强技术来更高效地使用带有标签的数据。在U-Net的结构中,包括捕获一个上下文信息的收缩路径和一个允许精确定位的对称拓展路径。这种方法可以使用非常少的数据完成端到端的训练,并获得最好的效果。其核心思想如下:
(1)提出了U-net这种网络结构。
它同时具有捕捉上下文信息的收缩路径和允许精确定位的对称扩展路径。
下采样+上采样+skip connection。
这里需要注意的是,FCN中深层信息与浅层信息融合是通过对应像素相加的方式,而Unet是通过拼接的方式。
(2)Overlap-tile策略。
这种方法用于补全输入图像的上下文信息,可以解决由于显存不足造成的图像分块输入的问题。
(3)使用随机弹性形变进行数据增强。
(4)使用加权损失。
预先计算权重图,一方面补偿了训练数据每类像素的不同频率,另一方面使网络更注重学习相互接触的细胞间的边缘。
二、论文内容
2.1 Introduction
CNN存在很久了,但是一直受限于过大的数据量和神经网络的规模,并没有获得很大的成功,直至Krizhevsky才开始爆发。但是将CNN用于生物医学图像存在着两点困难,首先CNN常用于分类,但是生物医学往往关注的是分割之类的定位任务;其次医学图像很难获得那么大规模的数据。
以往解决上面两点困难的方法是使用滑窗的方法,为每一个待分类的像素点取周围的一部分邻域输入。这样的方法有两点好处,首先它完成了定位的工作,其次因为每次取一个像素点周围的邻域,所以大大增加了训练数据的数量。但是这样的方法也有两个缺点,首先通过滑窗所取的块之间具有较大的重叠,所以会导致速度变慢(由FCN的论文分析可知,前向传播和反向传播的速度都会变慢);其次是网络需要在局部准确性和获取上下文之间进行取舍(局部信息和上下文信息之间是矛盾的)。因为更大的块需要更多的池化层进而降低了定位的准确率,但是小的块使网络只看到很小的一部分上下文。现在一种常见的作法是将多个层放在一起进行考虑(比如说FCN)。
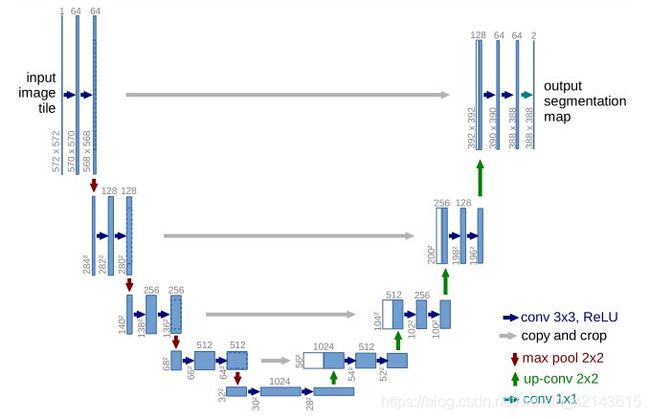
作者修改并延展了FCN的网络结构,使之在仅使用少量的数据进行训练的情况下获得精确的分割结果,具体结构如图1所示:
图1 U-net网络结构图
如上图所示,这里我们假设U-net的最低分辨率为32*32。每一个蓝色的块代表一个多通道的特征图。特征图的通道数被标注在块的顶部。X-Y尺寸设置在块的左下边缘。箭头代表着不同的操作。其中左半部分是收缩路径,右半部分扩展路径。
def unet(pretrained_weights=None, input_size=(256, 256, 1)):
inputs = Input(input_size) # 初始化keras张量
conv1 = Conv2D(64, 3, activation='relu', padding='same', kernel_initializer='he_normal')(inputs)
# filters:输出的维度
# kernel_size:卷积核的尺寸
# activation:激活函数
# padding:边缘填充
# kernel_initializer:kernel权值初始化
conv1 = Conv2D(64, 3, activation='relu', padding='same', kernel_initializer='he_normal')(conv1)
pool1 = MaxPooling2D(pool_size=(2, 2))(conv1)
conv2 = Conv2D(128, 3, activation='relu', padding='same', kernel_initializer='he_normal')(pool1)
conv2 = Conv2D(128, 3, activation='relu', padding='same', kernel_initializer='he_normal')(conv2)
pool2 = MaxPooling2D(pool_size=(2, 2))(conv2)
conv3 = Conv2D(256, 3, activation='relu', padding='same', kernel_initializer='he_normal')(pool2)
conv3 = Conv2D(256, 3, activation='relu', padding='same', kernel_initializer='he_normal')(conv3)
pool3 = MaxPooling2D(pool_size=(2, 2))(conv3)
conv4 = Conv2D(512, 3, activation='relu', padding='same', kernel_initializer='he_normal')(pool3)
conv4 = Conv2D(512, 3, activation='relu', padding='same', kernel_initializer='he_normal')(conv4)
drop4 = Dropout(0.5)(conv4) # 每次训练时随机忽略50%的神经元,减少过拟合
pool4 = MaxPooling2D(pool_size=(2, 2))(drop4)
conv5 = Conv2D(1024, 3, activation='relu', padding='same', kernel_initializer='he_normal')(pool4)
conv5 = Conv2D(1024, 3, activation='relu', padding='same', kernel_initializer='he_normal')(conv5)
drop5 = Dropout(0.5)(conv5)
up6 = Conv2D(512, 2, activation='relu', padding='same', kernel_initializer='he_normal')(
UpSampling2D(size=(2, 2))(drop5)) # 先上采样放大,在进行卷积操作,相当于转置卷积
# merge6 = merge([drop4, up6], mode='concat', concat_axis=3)
merge6 = concatenate([drop4, up6], axis=3) # (width,heigth,channels)拼接通道数
conv6 = Conv2D(512, 3, activation='relu', padding='same', kernel_initializer='he_normal')(merge6)
conv6 = Conv2D(512, 3, activation='relu', padding='same', kernel_initializer='he_normal')(conv6)
up7 = Conv2D(256, 2, activation='relu', padding='same', kernel_initializer='he_normal')(
UpSampling2D(size=(2, 2))(conv6))
# merge7 = merge([conv3, up7], mode='concat', concat_axis=3)
merge7 = concatenate([conv3, up7], axis=3)
conv7 = Conv2D(256, 3, activation='relu', padding='same', kernel_initializer='he_normal')(merge7)
conv7 = Conv2D(256, 3, activation='relu', padding='same', kernel_initializer='he_normal')(conv7)
up8 = Conv2D(128, 2, activation='relu', padding='same', kernel_initializer='he_normal')(
UpSampling2D(size=(2, 2))(conv7))
# merge8 = merge([conv2, up8], mode='concat', concat_axis=3)
merge8 = concatenate([conv2, up8], axis=3)
conv8 = Conv2D(128, 3, activation='relu', padding='same', kernel_initializer='he_normal')(merge8)
conv8 = Conv2D(128, 3, activation='relu', padding='same', kernel_initializer='he_normal')(conv8)
up9 = Conv2D(64, 2, activation='relu', padding='same', kernel_initializer='he_normal')(
UpSampling2D(size=(2, 2))(conv8))
# merge9 = merge([conv1, up9], mode='concat', concat_axis=3)
merge9 = concatenate([conv1, up9], axis=3)
conv9 = Conv2D(64, 3, activation='relu', padding='same', kernel_initializer='he_normal')(merge9)
conv9 = Conv2D(64, 3, activation='relu', padding='same', kernel_initializer='he_normal')(conv9)
conv9 = Conv2D(2, 3, activation='relu', padding='same', kernel_initializer='he_normal')(conv9)
conv10 = Conv2D(1, 1, activation='sigmoid')(conv9)
model = Model(input=inputs, output=conv10)
model.compile(optimizer=Adam(lr=1e-4), loss='binary_crossentropy', metrics=['accuracy'])
# optimizer:优化器
# binary_crossentropy:与sigmoid相对应的损失函数
# metrics:评估模型在训练和测试时的性能的指标卷积层:无填充卷积+relu+(2*2,stride=2)的max pooling;
卷积滤波器的数量每次下采样后double。
patch:上采样的时候是下采样时候的两倍。因为要把下采样的patch合并过来。
FCN的主要思想是使用连续的层补充通常的收缩网络,其中的池化层被上采样层取代。因此这些增加了输出层的分辨率。为了定位,来自收缩路径的高分辨率与上采样输出相结合。基于这个信息,一个连续的卷积层可以学习组装(集成)更精确的输出。
U-net与FCN的不同在于,U-net的上采样依然有大量的通道,这使得网络将上下文信息向更高层分辨率传播。作为结果,扩展路径多多少少与收缩路径对称,形成一个U的形状。网络没有全连接层并且只是用每一个卷积层的有效部分,例如分割图(指图像的输出)只包含这样的一些像素点,它们的上下文(它周围的像素点)都出现在了输入图像中。这种策略使得我们通过一个Overlap-tile策略可以使得任意大小的输入图像都可以获得一个无缝分割。Overlap-tile策略如图2所示:
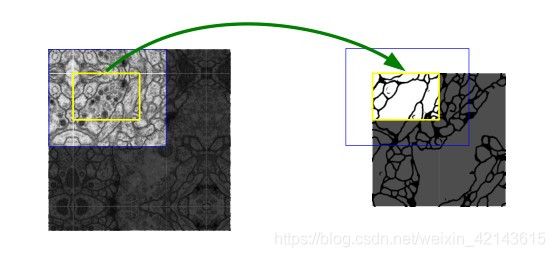
图2 Overlap-tile策略示意图
上图是针对任意大小的输入图像的无缝分割的Overlap-tile策略。如果我们要预测黄色框内区域(即对黄色的内的细胞进行分割,获取它们的边缘),需要将蓝色框内部分作为输入。缺失的数据使用镜像进行补充。因为进行的是valid卷积(即上文讲的只取有效部分,可以理解为0 padding),所以需要取比黄色框大的图像来保证上下文的信息是有意义的,缺失的部分用镜像的方法补充是填充上下文信息最好的方法了。
Valid卷积可参考:https://blog.csdn.net/leviopku/article/details/80327478
或许你会有一个问题,为什么作为一种全卷积神经网络不直接输入整张图像,还在做分块呢?答案是因为内存限制,需要分块输入。虽然还是要分块处理,但比之前的滑窗取块要好很多,一方面不用取那么多块,另一方面块之间也没有那么大的区域重叠。通过Overlap-tile策略可以将图像分块输入,否则的话就只能对图像进行resize了,但是这样会降低输入图像的分辨率。
应用弹性形变进行大量的数据增强。这允许网络可以学习到这种形变的不变性,并且并不要求在带有标签的原始语料库进到这样的变化(指弹性形变)。
弹性形变可参考:https://zhuanlan.zhihu.com/p/46833956
进行细胞的分割,另一种挑战是同一类物体的分类,如下图所示:
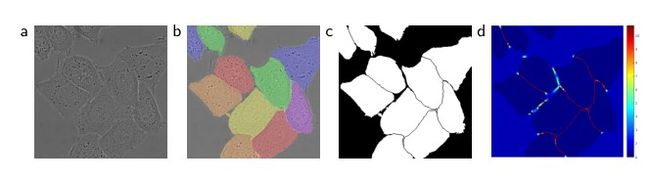
图3 像素点分类权重示意图
上图是用DIC(二次干涉对比)显微技术记录的玻璃上的HeLa细胞。其中图(a)是原始图像;图(b)是基于gt的分割覆盖。其中不同的颜色表示不同的HeLa细胞示例。图(c)是生成的分割掩膜,其中白色部分是前景,黑色部分是后景;图(d)是像素级损失权重图,使得网络强制学习边缘像素。
为了解决这个问题,作者使用加权损失,对于位于细胞接触部分的像素加大权重,如图(d)中的红色的部分。
2.2 Network Architecture
网络结构就是最上面的那张图,其中需要注意的是,每经过一次上采样都会将通道数减半,再与收缩路径对应的特征图进行拼接。在拼接之前进行crop是必要的,因为两者的尺寸并不相同(主要是因为valid conv造成的)。最后一层使用1×1大小的卷积核,将通道数降低至特定的数量(如像素点的类别数量)。
网络对于输入的大小也是有要求的。为了使得输出的分割图无缝拼接,重要的是选择输入块的大小,以便所有的2×2的池化层都可以应用于偶数的x层和y层。一个比较好的方法是从最下的分辨率从反向推到,比如说在网络结构中,最小的是32×32,沿着收缩路径的反向进行推导可知,输入图像的尺寸应该为572×572。
2.3 Training
作者使用caffe框架,并且采用带动量的随机梯度下降(SGD)方法,其中动量的值设为momentum=0.99。动量设这么大的原因是这样可以使用大量先前看到的训练样本确定当前最优步骤中的更新。相比于大的batchsize,作者喜欢大的input tiles(指的是oveelap-tile)中的那种图像块,因此我们可以将一个batch缩小为一个当张图片的输入。
通过在最后最后的特征图上softmax的输出结果计算交叉熵损失函数,以此来作为整个网络的能量函数。其中soft-max输出层的计算方法如下:
其中需要注意的是这里使用的是加权的损失函数,对于每一个像素点有着自己的权重,这点可以在图3中看到。
作者通过预先计算权重图的来获得每一个像素在损失函数中的权值,这种方法补偿了训练数据每类像素的不同频率,并且使网络更注重学习相互接触的细胞间的边缘。分割边界使用形态学运算,特征图的计算方法如下:
其中wc的是用于平衡类别频率的权重图,d1是该像素点到最近的细胞边界的距离;d2是该像素点到第二近的细胞边界的距离。在我们的实验中,将w0设置为10,将σc设置为大约5个像素。
初始化对于模型的正确训练起着很大的作用,一个好的初始化应该保证网络中的每一个特征图有近似的单位方差。在这里使用服从标准差为![]() 的高斯分布来进行初始化,其中的N代表着一个神经元的传入节点的数目,比如说某一个卷积层,他的卷积核的大小为3×3,通道数是64,那么N=9×64=576。
的高斯分布来进行初始化,其中的N代表着一个神经元的传入节点的数目,比如说某一个卷积层,他的卷积核的大小为3×3,通道数是64,那么N=9×64=576。
优化器:SGD,0.99的动量系数;
loss:cross entropy loss function;
输入:尽可能大的batch来完美使用GPU内存。
权重初始化:高斯(0,sigma=sqrt(2/N));
图像增强弹性形变。
2.4 Data Augmentation
当只有少量的训练样本,对于让网络学习到所需的不变性和鲁棒性来讲,数据增强是必要的。这里尤其需要注意的是,这里指的少量数据样本究竟少到一种什么样的程度,就IBSI 2012数据集来讲,它仅仅有30张512×512的图像作为训练集!
显微图像一般需要旋转平移不变性,弹性形变和灰度值变化鲁棒性。训练样本的随机弹性形变似乎是训练之后少量标注图像的分割网络的关键。此外在收缩路径的最后加入了Drop-out,隐式地加强了数据增强。
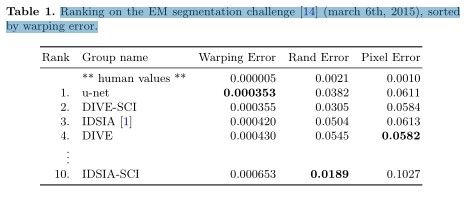
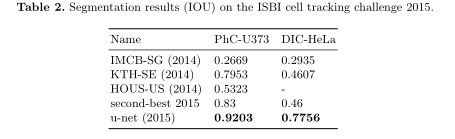
2.5 Experiments
作者演示了u-net在三个不同细分任务中的应用。第一项任务是在电子显微镜记录中分割神经元结构。作者还将u-net应用于光学显微图像中的细胞分割任务。
三、总结
主要是提出了U-net这种网络结构。它同时具有捕捉上下文信息的收缩路径和允许精确定位的对称扩展路径;并且与FCN相比,U-net的上采样依然有大量的通道,这使得网络将上下文信息向更高层分辨率传播。借助具有弹性变形功能的数据增强功能,它只需要很少的带注释的图像,就能有很好的效果。
3.1 实践中需要注意的技巧
(1)因为使用了valid conv,所以采用Overlap-tile策略补充图像,其中空白的部分用镜像的方法进行补充。
(2)因为有池化层,因此要保证输入的图像在经过每一次池化的时候都要是边长偶数。这点与与一般的卷积神经网络不同,因为一般的网络会使用padding,这样会保证卷积前后的大小不变,但是valid conv会使卷积后的尺寸变小,所以要特别注意输入图像的尺寸。一个比较好的方法是从最小分辨率出发沿收缩路径的反方向进行计算,得到输入图像的尺寸。
(3)预先计算权重图,以此计算后面的加权损失函数。
(4)加权损失的权重中有一部分是经验值,因此对于不同的任务可以进行调整(只是理论上可以进行调整,并没有试验过)。
(5)使用标准差为![]() 的高斯分布来进行初始化,其中需要注意的是,对于不同的卷积层,N的大小也是不同的。
的高斯分布来进行初始化,其中需要注意的是,对于不同的卷积层,N的大小也是不同的。
(6)在收缩路径的最后部加入了drop-out,隐式地加强了数据增强。